python3 ok -q swap
Copy
✂️

Regex

Q4: Address First Line

Write a regular expression that parses strings and returns whether it contains the first line of a US mailing address.

US mailing addresses typically contain a block number, which is a sequence of 3-5 digits, following by a street name. The street name can consist of multiple words but will always end with a street type abbreviation, which itself is a sequence of 2-5 English letters. The street name can also optionally start with a cardinal direction ("N", "E", "W", "S"). Everything should be properly capitalized.

Proper capitalization means that the first letter of each name is capitalized. It is fine to have things like "WeirdCApitalization" match.

See the doctests for some examples.

def address_oneline(text):
    """
    Finds and returns if there are expressions in text that represent the first line
    of a US mailing address.

    >>> address_oneline("110 Sproul Hall, Berkeley, CA 94720")
    True
    >>> address_oneline("What's at 39177 Farwell Dr? Is there a 39177 Nearwell Dr?")
    True
    >>> address_oneline("I just landed at 780 N McDonnell Rd, and I need to get to 1880-ish University Avenue. Help!")
    True
    >>> address_oneline("123 Le Roy Ave")
    True
    >>> address_oneline("110 Unabbreviated Boulevard")
    False
    >>> address_oneline("790 lowercase St")
    False
    """
    block_number = r'___'
    cardinal_dir = r'___' # whitespace is important!
    street = r'___'
    type_abbr = r'___'
    street_name = f"{cardinal_dir}{street}{type_abbr}"
    return bool(re.search(f"{block_number} {street_name}", text))

Use Ok to test your code:

python3 ok -q address_oneline
Copy
✂️

BNF

Q5: WWPD: PyCombinator

Consider this attempt at a BNF grammar for Pycombinator, a grammar which supports a subset of Python's functionality. Specifically, it is able to parse any expression with a Python arithmetic operator. The grammar is specified below:

?start: pycomb_expression

pycomb_expression: func "(" arg ("," arg)* ")"

arg: pycomb_expression | NUMBER

func: FUNCNAME

FUNCNAME: "add" | "mul" | "sub"

%ignore " "
%import common.NUMBER

Let's understand and modify the functionality of this BNF with a few questions.

Use Ok to test your knowledge by choosing the best answer for each of the following "What Would PyCombinator Do" questions:

python3 ok -q wwpd-bnf -u

Submit

Make sure to submit this assignment by running:

python3 ok --submit

Recommended Questions

The following problems are not required for credit on this lab but may help you prepare for the final.

Trees

Q6: Prune Min

Write a function that prunes a Tree t mutatively. t and its branches always have zero or two branches. For the trees with two branches, reduce the number of branches from two to one by keeping the branch that has the smaller label value. Do nothing with trees with zero branches.

Prune the tree in a direction of your choosing (top down or bottom up). The result should be a linear tree.

def prune_min(t):
    """Prune the tree mutatively.

    >>> t1 = Tree(6)
    >>> prune_min(t1)
    >>> t1
    Tree(6)
    >>> t2 = Tree(6, [Tree(3), Tree(4)])
    >>> prune_min(t2)
    >>> t2
    Tree(6, [Tree(3)])
    >>> t3 = Tree(6, [Tree(3, [Tree(1), Tree(2)]), Tree(5, [Tree(3), Tree(4)])])
    >>> prune_min(t3)
    >>> t3
    Tree(6, [Tree(3, [Tree(1)])])
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q prune_min
Copy
✂️

Q7: Add trees

Define the function add_trees, which takes in two trees and returns a new tree where each corresponding node from the first tree is added with the node from the second tree. If a node at any particular position is present in one tree but not the other, it should be present in the new tree as well.

Hint: You may want to use the built-in zip function to iterate over multiple sequences at once.

def add_trees(t1, t2):
    """
    >>> numbers = Tree(1,
    ...                [Tree(2,
    ...                      [Tree(3),
    ...                       Tree(4)]),
    ...                 Tree(5,
    ...                      [Tree(6,
    ...                            [Tree(7)]),
    ...                       Tree(8)])])
    >>> print(add_trees(numbers, numbers))
    2
      4
        6
        8
      10
        12
          14
        16
    >>> print(add_trees(Tree(2), Tree(3, [Tree(4), Tree(5)])))
    5
      4
      5
    >>> print(add_trees(Tree(2, [Tree(3)]), Tree(2, [Tree(3), Tree(4)])))
    4
      6
      4
    >>> print(add_trees(Tree(2, [Tree(3, [Tree(4), Tree(5)])]), \
    Tree(2, [Tree(3, [Tree(4)]), Tree(5)])))
    4
      6
        8
        5
      5
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q add_trees
Copy
✂️

Objects

Let's implement a game called Election. In this game, two players compete to try and earn the most votes. Both players start with 0 votes and 100 popularity.

The two players alternate turns, and the first player starts. Each turn, the current player chooses an action. There are two types of actions:

• The player can debate, and either gain or lose 50 popularity. If the player has popularity p1 and the other player has popularity p2, then the probability that the player gains 50 popularity is max(0.1, p1 / (p1 + p2)) Note that the max causes the probability to never be lower than 0.1.
• The player can give a speech. If the player has popularity p1 and the other player has popularity p2, then the player gains p1 // 10 votes and popularity and the other player loses p2 // 10 popularity.

The game ends when a player reaches 50 votes, or after a total of 10 turns have been played (each player has taken 5 turns). Whoever has more votes at the end of the game is the winner!

Q8: Player

First, let's implement the Player class. Fill in the debate and speech methods, that take in another Player other, and implement the correct behavior as detailed above. Here are two additional things to keep in mind:

• In the debate method, you should call the provided random function, which returns a random float between 0 and 1. The player should gain 50 popularity if the random number is smaller than the probability described above, and lose 50 popularity otherwise.
• Neither players' popularity should ever become negative. If this happens, set it equal to 0 instead.

### Phase 1: The Player Class
class Player:
    """
    >>> random = make_test_random()
    >>> p1 = Player('Hill')
    >>> p2 = Player('Don')
    >>> p1.popularity
    100
    >>> p1.debate(p2)  # random() should return 0.0
    >>> p1.popularity
    150
    >>> p2.popularity
    100
    >>> p2.votes
    0
    >>> p2.speech(p1)
    >>> p2.votes
    10
    >>> p2.popularity
    110
    >>> p1.popularity
    135

    """
    def __init__(self, name):
        self.name = name
        self.votes = 0
        self.popularity = 100

    def debate(self, other):
        "*** YOUR CODE HERE ***"

    def speech(self, other):
        "*** YOUR CODE HERE ***"

    def choose(self, other):
        return self.speech

Use Ok to test your code:

python3 ok -q Player
Copy
✂️

Q9: Game

Now, implement the Game class. Fill in the play method, which should alternate between the two players, starting with p1, and have each player take one turn at a time. The choose method in the Player class returns the method, either debate or speech, that should be called to perform the action.

In addition, fill in the winner method, which should return the player with more votes, or None if the players are tied.

### Phase 2: The Game Class
class Game:
    """
    >>> p1, p2 = Player('Hill'), Player('Don')
    >>> g = Game(p1, p2)
    >>> winner = g.play()
    >>> p1 is winner
    True

    """
    def __init__(self, player1, player2):
        self.p1 = player1
        self.p2 = player2
        self.turn = 0

    def play(self):
        while not self.game_over():
            "*** YOUR CODE HERE ***"
        return self.winner()

    def game_over(self):
        return max(self.p1.votes, self.p2.votes) >= 50 or self.turn >= 10

    def winner(self):
        "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q Game
Copy
✂️

Q10: New Players

The choose method in the Player class is boring, because it always returns the speech method. Let's implement two new classes that inherit from Player, but have more interesting choose methods.

Implement the choose method in the AggressivePlayer class, which returns the debate method if the player's popularity is less than or equal to other's popularity, and speech otherwise. Also implement the choose method in the CautiousPlayer class, which returns the debate method if the player's popularity is 0, and speech otherwise.

### Phase 3: New Players
class AggressivePlayer(Player):
    """
    >>> random = make_test_random()
    >>> p1, p2 = AggressivePlayer('Don'), Player('Hill')
    >>> g = Game(p1, p2)
    >>> winner = g.play()
    >>> p1 is winner
    True

    """
    def choose(self, other):
        "*** YOUR CODE HERE ***"

class CautiousPlayer(Player):
    """
    >>> random = make_test_random()
    >>> p1, p2 = CautiousPlayer('Hill'), AggressivePlayer('Don')
    >>> p1.popularity = 0
    >>> p1.choose(p2) == p1.debate
    True
    >>> p1.popularity = 1
    >>> p1.choose(p2) == p1.debate
    False

    """
    def choose(self, other):
        "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q AggressivePlayer
python3 ok -q CautiousPlayer
Copy
✂️

Lists

Q11: Intersection - Summer 2015 MT1 Q4

Implement intersection(lst_of_lsts), which takes a list of lists and returns a list of distinct elements that appear in all the lists in lst_of_lsts. If no number appears in all of the lists, return the empty list. You may assume that lst_of_lsts contains at least one list.

def intersection(lst_of_lsts):
    """Returns a list of distinct elements that appear in every list in
    lst_of_lsts.

    >>> lsts1 = [[1, 2, 3], [1, 3, 5]]
    >>> intersection(lsts1)
    [1, 3]
    >>> lsts2 = [[1, 4, 2, 6], [7, 2, 4], [4, 4]]
    >>> intersection(lsts2)
    [4]
    >>> lsts3 = [[1, 2, 3], [4, 5], [7, 8, 9, 10]]
    >>> intersection(lsts3)         # No number appears in all lists
    []
    >>> lsts4 = [[3, 3], [1, 2, 3, 3], [3, 4, 3, 5]]
    >>> intersection(lsts4)         # Return list of distinct elements
    [3]
    """
    elements = []
    "*** YOUR CODE HERE ***"
    return elements

Use Ok to test your code:

python3 ok -q intersection
Copy
✂️

Q12: Deck of cards

Write a list comprehension that will create a deck of cards, given a list of suits and a list of ranks. Each element in the list will be a card, which is represented by a 2-element list of the form [suit, rank].

def deck(suits, ranks):
    """Creates a deck of cards (a list of 2-element lists) with the given
    suits and ranks. Each element in the returned list should be of the form
    [suit, rank].

    >>> deck(['S', 'C'], [1, 2, 3])
    [['S', 1], ['S', 2], ['S', 3], ['C', 1], ['C', 2], ['C', 3]]
    >>> deck(['S', 'C'], [3, 2, 1])
    [['S', 3], ['S', 2], ['S', 1], ['C', 3], ['C', 2], ['C', 1]]
    >>> deck([], [3, 2, 1])
    []
    >>> deck(['S', 'C'], [])
    []
    """
    "*** YOUR CODE HERE ***"
    return ______

Use Ok to test your code:

python3 ok -q deck
Copy
✂️

Linked Lists

Q13: O!-Pascal - Fall 2017 Final Q4

Pasal's Triangle is perhaps familiar to you from the diagram below, which shows the first five rows.

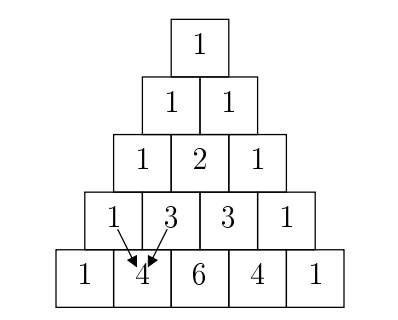
Every square is the sum of the two squares above it (as illustrated by the arrows showing here the value 4 comes from), unless it doesn't have two squares above it, in whih case its value is 1.

Given a linked list that represents a row in Pasal's triangle, return a linked list that will represent the row below it.

def pascal_row(s):
    """
    >>> a = Link.empty
    >>> for _ in range(5):
    ...     a = pascal_row(a)
    ...     print(a)
    <1>
    <1 1>
    <1 2 1>
    <1 3 3 1>
    <1 4 6 4 1>
    """
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q pascal_row
Copy
✂️