CS61A Homework 2
Due by 11:59 PM on (that is, the end of) Tuesday, 6/26
This homework must be submitted online. We do not require a paper copy.
To turn in the electronic copy, submit all of your answers in a file named hw2.py. Follow the instructions here to submit the electronic copy.
Readings. All problems in this homework can be solved with the subset of Python 3 introduced in sections 1.1-1.6 of the lecture notes. We also use the round function for a few tests, which takes a number and a number of decimal digits to round that number to. For example, round(6.66666666, 3) evaluates to 6.667
If you would like, you can use the template file hw2.py.
To copy this file to your lab account you can run the command:
cp ~cs61a/lib/hw/hw02/hw2.py .
to copy it into your current directory.
Q1. Define a function double that takes a function of one argument as an argument, and returns a function that applies the original function twice. For example, if increment is a function that returns 1 more than its argument, then double(inc) should be a function that returns two more:
def double(f):
"""Return a function that applies f twice.
>>> increment = lambda x: x + 1
>>> add_two = double(increment)
>>> add_two(2)
4
>>> double(lambda x: x + 2)(2)
6
"""
Q2. If f is a numerical function and n is a positive integer, then we can form the nth repeated application of f, which is defined to be the function whose value at x is f(f(...(f(x))...)), where f is used n times. For example, if f adds 1 to its argument, then the nth repeated application of f adds n. Write a function that takes as inputs a function f and a positive integer n and returns the function that computes the nth repeated application of f:
def repeated(f, n):
"""Return the function that computes the nth application of f.
>>> increment = lambda x: x + 1
>>> add_five = repeated(increment, 5)
>>> add_five(6)
11
>>> repeated(lambda x: x + 2, 7)(6)
20
>>> repeated(square, 2)(5)
625
"""
Your function should produce the same results as those shown in the doctest. Hint: You may find it convenient to use compose1 from the lecture notes.
Q3. The idea of smoothing a function is an important concept in signal processing. If f is a one-argument function and dx is some small number, then the smoothed version of f is the function whose value at a point x is the average of f(x - dx), f(x), and f(x + dx). Write a function smooth that takes as input a function that computes f and a value to use for dx and returns a function that computes the smoothed f.
def smooth(f, dx):
"""Returns the smoothed version of f, g where
g(x) = (f(x - dx) + f(x) + f(x + dx)) / 3
>>> round(smooth(square, 1)(0), 3)
0.667
"""
It is sometimes valuable to repeatedly smooth a function (that is, smooth the smoothed function, and so on) to obtained the n-fold smoothed function. Show how to generate the n-fold smoothed function, n_fold_smooth, of any given function using your smooth function and repeated from question 2.
def n_fold_smooth(f, dx, n):
"""Returns the n-fold smoothed version of f
>>> square = lambda x: x ** 2
>>> round(n_fold_smooth(square, 1, 3)(0), 3)
2.0
"""
Q4. An infinite continued fraction is an expression of the form:
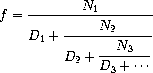
As an example, one can show that the inverse of the golden ratio can be computed by setting all of the terms to 1. A way to approximate the value of an infinite continued fraction is to compute the value of truncating after a given number of terms. This truncation, called the k-term finite continued fraction, has the form:
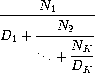
Write the function continued_frac, which takes two functions n_term and d_term, which each produce the ith N and D term respectively, and a number k and returns the k-term finite continued fraction.
def continued_frac(n_term, d_term, k):
"""Returns the k-term continued fraction with numerators defined by n_term
and denominators defined by d_term.
>>> # golden ratio
... round(continued_frac(lambda x: 1, lambda x: 1, 8), 3)
0.618
>>> # 1 / (1 + (2 / (2 + (3 / (3 + (4 / 4))))))
... round(continued_frac(lambda x: x, lambda x: x, 4), 6)
0.578947
"""
Using this, you should be able to approximate the value of the golden ratio up to 3 decimal digits as shown in the first doctest.
Extra for Experts:
Note: "Extra for Experts" problems are completely optional. You are encouraged to try these questions. However, these are questions which we consider more difficult than what we would consider asking you on an exam, so please don't be discouraged if you don't solve them.
Q5. The logician Alonzo Church invented a system of representing non-negative integers entirely using functions. Here are the definitions of 0, and a function that returns 1 more than its argument:
def zero(f):
return lambda x: x
def successor(n):
return lambda f: lambda x: f(n(f)(x))
This representation is known as Church numerals. Define one and two directly, which are also functions. To get started, apply successor to zero. Then, give a direct definition of the add function (not in terms of repeated application of successor) over Church numerals. Finally, implement a function church_to_int that converts a church numeral argument to a regular Python int.
It is easy to find answers to this question on the Internet. Try to solve it on your own before looking it up!