This lab has some orders of growth examples, sample tree data structures for you to use, as well as a template to fill in for the questions. To get this template file, execute in your terminal:
cp ~cs61a/public_html/su13/lab/lab05a/lab05a*.py .
Computer scientists are often interested in the efficiency of a program – how much more expensive it is to run some procedure with a larger input. In other words, as the size of the input grows, how do the speed of the procedure and the space its process occupies grow?
To give a useful idea of efficiency, we use the Big-Theta notation. For example, if foo's running time is in Θ(n2), the running time, R(n) will grow proportionally to the square of the size of the input.
We will see more examples of this in discussion, but for now, let's take a look at the running times of some code. The lab05a_timer.py file has some code and also a function that will test the running times of various procedures: mapping onto an Rlist and also calculating the Fibonacci numbers. Run the file by executing:
python3 lab05a_timer.py
Try to analyze why some functions are faster than others. We will discuss this more in depth tomorrow.
Trees are a way we have of representing a hierarchy of information. A family tree is a good example of something with a tree structure. You have a matriarch and a patriarch followed by all the descendants. Alternately, we may want to organize a series of information geographically. At the very top, we have the world, but below that we have countries, then states, then cities. We can also decompose arithmetic operations into something much the same way.
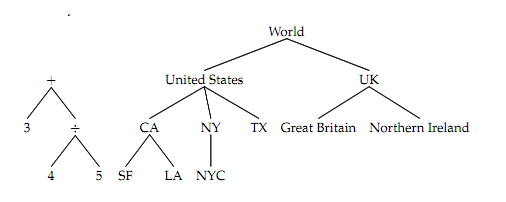
The name "tree" comes from the branching structure of the pictures, like real trees in nature except that they’re drawn with the root at the top and the leaves at the bottom.
node - a point in the tree. In these pictures, each node includes a label (value at each node) root - the node at the top. Every tree has one root node children - the nodes directly beneath it. Arity is the number of children that node has. leaf - a node that has no children. (Arity of 0!)
In this course, we will only be working with binary trees, where each node as at most two children. For a general binary tree, order does not matter. Additionally, the tree does not have to be balanced. It can be as lopsided as one long chain.
Take a moment to study our implementation of binary trees. The implementation of trees is in the file ~cs61a/public_html/su13/lab/lab05a/tree.py.
Define the function max_of_tree which takes in a tree as an argument and returns the max of all of the values of each node in the tree.
>>> t Tree(4, Tree(2, Tree(8, Tree(7), None), Tree(3, Tree(1), Tree(6))), Tree(1, Tree(5), Tree(3, Tree(2), Tree(9)))) >>> max_of_tree(t) 9
Define the function size_of_tree which takes in a tree as an argument and returns the number of non-empty nodes in the tree.
>>> t Tree(4, Tree(2, Tree(8, Tree(7), None), Tree(3, Tree(1), Tree(6))), Tree(1, Tree(5), Tree(3, Tree(2), Tree(9)))) >>> size_of_tree(t) 12
Define the function deep_tree_reverse, which takes a tree and reverses the given order.
>>> a = t.copy() >>> deep_tree_reverse(a) >>> a Tree(4, Tree(1, Tree(3, Tree(9), Tree(2)), Tree(5)), Tree(2, Tree(3, Tree(6), Tree(1)), Tree(8, None, Tree(7))))
Define the function filter_tree which takes in a tree as an argument and returns the same tree, but with items included or excluded based on the pred argument.
Note that there is ambiguity about what excluding a tree means. For this function, when you exclude a subtree, you exclude all of its children as well.
>>> a = t.copy() >>> filter_tree(a, lambda x: x % 2 == 0) Tree(4, Tree(2, Tree(8), None), None) >>> a = t.copy() >>> filter_tree(a, lambda x : x > 2) Tree(4)
Binary search trees are a special case of regular trees that are useful for organizing data and searching through it efficiently. Binary search trees have 2 special properties apart from regular trees:
To illustrate this, first, draw these trees out on a piece of paper. Then, determine if the trees are valid binary search trees. Some are solved for you, and the rest are given to you as an exercise.
Note: str(bst) prints out the left subtree first, and then the right subtree.
VALID >>> bst_a Tree(3, Tree(1, Tree(0), None), Tree(5, Tree(4), None))
INVALID
>>> bst_b
Tree(1, Tree(3, Tree(0), None), Tree(5, Tree(4), None))
>>> bst_c
Tree(6, Tree(5, Tree(4, Tree(3, Tree(2, Tree(1), None), None), None), None), None)
>>> bst_d
Tree(5, Tree(4, Tree(1, Tree(2), None), None), Tree(9, Tree(6, Tree(8, Tree(7), None), None), None))
Write a function is_valid_bst, that takes a given bst, and returns True if the bst is a valid binary search tree; that is, for every node, that node's left children are less than the node, and that node's right children are greater than that node. You might find the get_min and get_max functions helpful. Test your function with the given binary search trees from above (these are already typed out in the lab9.py file) to make sure your function works properly.
Write a function bst_find which takes two arguments, bst and elem. bst_find should return True if elem is in the tree and False if it is not.
Write a function bst_count_num which takes two arguments, bst and max. bst_count_num should return the number of items in the tree that are less than the given max. Implement bst_count in the following ways:
Write a function is_right_bigger, which takes a single argument bst, and returns whether or not the right subtree in this bst is larger (has more items) than the left subtree.
>>> is_right_bigger(bst_c) False >>> is_right_bigger(bst_d) True