Lab 09: Mutable Trees
Due at 11:59pm on Friday, 07/20/2018.
Lab Check-in 5 questions here.
Starter Files
Download lab09.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the Ok autograder.
Submission
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
Check that you have successfully submitted your code on
okpy.org.
- Questions 1 through 4 must be completed in order to receive credit for this lab. Starter code for coding questions is in lab09.py.
- Questions 5 and 6 are optional. It is recommended that you complete these problems on your own time. Starter code for these questions is in lab09_extra.py.
Topics
Trees (Again)
Recall that a tree is a recursive abstract data type that has a label (the
value stored in the root of the tree) and branches (a list of trees directly
underneath the root).
We saw one way to implement the tree ADT -- using constructor and selector
functions that treat trees as lists. Another, more formal, way to implement the
tree ADT is with a class. Here is part of the class definition for Tree,
which can be found in lab09.py:
class Tree:
"""
>>> t = Tree(3, [Tree(2, [Tree(5)]), Tree(4)])
>>> t.label
3
>>> t.branches[0].label
2
>>> t.branches[1].is_leaf()
True
"""
def __init__(self, label, branches=[]):
for b in branches:
assert isinstance(b, Tree)
self.label = label
self.branches = list(branches)
def is_leaf(self):
return not self.branchesEven though this is a new implementation, everything we know about the tree ADT remains true. That means that solving problems involving trees as objects uses the same techniques that we developed when first studying the tree ADT (e.g. we can still use recursion on the branches!). The main difference, aside from syntax, is that tree objects are mutable.
Here is a summary of the differences between the tree ADT implemented using functions and lists vs. implemented using a class:
| - | Tree constructor and selector functions | Tree class |
|---|---|---|
| Constructing a tree | To construct a tree given a label and a list of branches, we call tree(label, branches) |
To construct a tree object given a label and a list of branches, we call Tree(label, branches) (which calls the Tree.__init__ method) |
| Label and branches | To get the label or branches of a tree t, we call label(t) or branches(t) respectively |
To get the label or branches of a tree t, we access the instance attributes t.label or t.branches respectively |
| Mutability | The tree ADT is immutable because we cannot assign values to call expressions | The label and branches attributes of a Tree instance can be reassigned, mutating the tree |
| Checking if a tree is a leaf | To check whether a tree t is a leaf, we call the convenience function is_leaf(t) |
To check whether a tree t is a leaf, we call the bound method t.is_leaf(). This method can only be called on Tree objects. |
Displaying Tree instances
Implementing trees as a class gives us another advantage: we can specify how we
want them to be output by the interpreter by implementing the __repr__ and
__str__ magic methods.
Here is the __repr__ method:
def __repr__(self):
if self.branches:
branch_str = ', ' + repr(self.branches)
else:
branch_str = ''
return 'Tree({0}{1})'.format(self.label, branch_str)With this implementation of __repr__, a Tree instance is displayed as the
exact constructor call that created it:
>>> t = Tree(4, [Tree(3), Tree(5, [Tree(6)]), Tree(7)])
>>> t
Tree(4, [Tree(3), Tree(5, [Tree(6)]), Tree(7)])
>>> t.branches
[Tree(3), Tree(5, [Tree(6)]), Tree(7)]
>>> t.branches[0]
Tree(3)
>>> t.branches[1]
Tree(5, [Tree(6)])Here is the __str__ method. You do not need to understand how this function
is implemented.
def __str__(self):
def print_tree(t, indent=0):
tree_str = ' ' * indent + str(t.label) + "\n"
for b in t.branches:
tree_str += print_tree(b, indent + 1)
return tree_str
return print_tree(self).rstrip()With this implementation of __str__, we can pretty-print a Tree to see
both its contents and structure:
>>> t = Tree(4, [Tree(3), Tree(5, [Tree(6)]), Tree(7)])
>>> print(t)
4
3
5
6
7
>>> print(t.branches[0])
3
>>> print(t.branches[1])
5
6Binary Search Trees
A binary search tree (or BST) is a special type of tree that obeys the following constraints:
- Each node has at most two branches, a left and a right branch.
- All labels in the left branch of any node have a value less than or equal to the label at that node.
- All labels in the right branch of any node have a value greater than the label at the node.
Thus, these are BSTs:
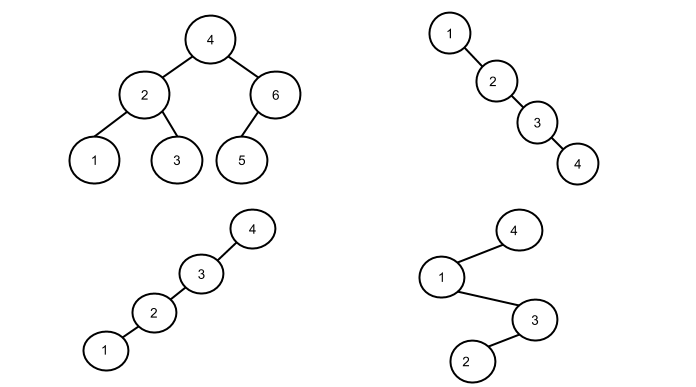
These are not BSTs:
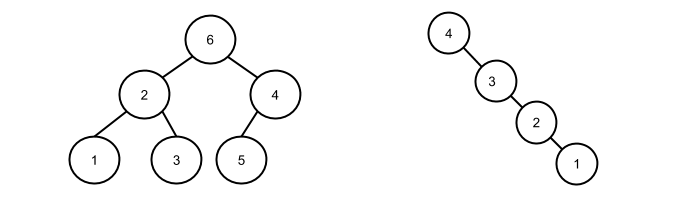
The following class implements BSTs. Because we constrain BSTs to have at most
two branches, we will store each branch as left and right instance
attributes rather than in a list. BST objects are recursive: each branch is
also a BST. Note that there exists an empty BST, which wasn't true with
regular trees; this allows us to construct trees with less than two branches.
class BST:
"""
>>> bst1 = BST(4, BST(2, BST(1)))
>>> bst1.max()
4
>>> bst1.min()
1
>>> bst2 = BST(6, BST(2, BST(1), BST(4)), BST(7, BST.empty, BST(9)))
>>> bst2.max()
9
>>> bst2.min()
1
>>> 9 in bst2
True
>>> 10 in bst2
False
>>> bst3 = BST(6, BST(2, BST(1), BST(4)), BST(8, BST(7), BST(9)))
>>> 7 in bst3
True
>>> 10 in bst3
False
"""
empty = ()
def __init__(self, label, left=empty, right=empty):
assert left is BST.empty or isinstance(left, BST)
assert right is BST.empty or isinstance(right, BST)
self.label = label
self.left, self.right = left, right
if left is not BST.empty:
assert left.max() <= label
if right is not BST.empty:
assert label < right.min()
def is_leaf(self):
return self.left is BST.empty and self.right is BST.empty
def __repr__(self):
if self.is_leaf():
return 'BST({0})'.format(self.label)
elif self.right is BST.empty:
left = repr(self.left)
return 'BST({0}, {1})'.format(self.label, left)
else:
left, right = repr(self.left), repr(self.right)
if self.left is BST.empty:
left = 'BST.empty'
template = 'BST({0}, {1}, {2})'
return template.format(self.label, left, right)
def max(self):
"""Returns max element in BST."""
if self.right is BST.empty:
return self.label
return self.right.max()
def min(self):
"""Returns min element in BST."""
if self.left is BST.empty:
return self.label
return self.left.min()
def __contains__(self, e):
if self.label == e:
return True
elif e > self.label and self.right is not BST.empty:
return e in self.right
elif self.left is not BST.empty:
return e in self.left
return FalseRequired Questions
What Would Python Display?
Q1: WWPD: Trees
Use Ok to test your knowledge with the following "What Would Python Display?" questions:
python3 ok -q trees -uEnter
Functionif you believe the answer is<function ...>,Errorif it errors, andNothingif nothing is displayed. Recall thatTreeinstances will be displayed the same way they are constructed.
>>> from lab07 import *
>>> t = Tree(1, Tree(2))
______Error
>>> t = Tree(1, [Tree(2)])
>>> t.label
______1
>>> t.branches[0]
______Tree(2)
>>> t.branches[0].label
______2
>>> t.label = t.branches[0].label
>>> t
______Tree(2, [Tree(2)])
>>> t.branches.append(Tree(4, [Tree(8)]))
>>> len(t.branches)
______2
>>> t.branches[0]
______Tree(2)
>>> t.branches[1]
______Tree(4, [Tree(8)])Coding Practice
Q2: Cumulative Sum
Write a function cumulative_sum that mutates the Tree t so that each node's
label becomes the sum of all labels in the subtree rooted at the node.
def cumulative_sum(t):
"""Mutates t so that each node's label becomes the sum of all labels in
the corresponding subtree rooted at t.
>>> t = Tree(1, [Tree(3, [Tree(5)]), Tree(7)])
>>> cumulative_sum(t)
>>> t
Tree(16, [Tree(8, [Tree(5)]), Tree(7)])
"""
"*** YOUR CODE HERE ***"
for b in t.branches:
cumulative_sum(b)
t.label = sum([b.label for b in t.branches]) + t.labelUse Ok to test your code:
python3 ok -q cumulative_sumQ3: Leaves
Write a function leaves that returns a list of all the label values of the
leaf nodes of a Tree.
def leaves(t):
"""Returns a list of all the labels of the leaf nodes of the Tree t.
>>> leaves(Tree(1))
[1]
>>> leaves(Tree(1, [Tree(2, [Tree(3)]), Tree(4)]))
[3, 4]
"""
"*** YOUR CODE HERE ***"
if t.is_leaf():
return [t.label]
all_leaves = []
for b in t.branches:
all_leaves += leaves(b)
return all_leavesUse Ok to test your code:
python3 ok -q leavesQ4: Insert
Implement the function insert, which takes in a BST and an value v and
inserts v into the correct position in the BST by mutating it.
Hint: Try drawing out a few examples of inserting into a BST. What do you notice about every node that is inserted? Will an inserted value ever become the label of an inner (i.e. non-leaf) node?
Note: To check if a BST is empty, compare its identity to
BST.empty:>>> b = BST(3, BST(2)) >>> b is BST.empty False >>> b.right is BST.empty True
def insert(bst, v):
"""
>>> bst = BST(5, BST(3, BST(1), BST(4)), BST(10, BST.empty, BST(11)))
>>> insert(bst, 2)
>>> 2 in bst
True
>>> insert(bst, 7)
>>> insert(bst, 6)
>>> bst
BST(5, BST(3, BST(1, BST.empty, BST(2)), BST(4)), BST(10, BST(7, BST(6)), BST(11)))
"""
"*** YOUR CODE HERE ***"
if v <= bst.label:
if bst.left is BST.empty:
bst.left = BST(v)
else:
insert(bst.left, v)
else:
if bst.right is BST.empty:
bst.right = BST(v)
else:
insert(bst.right, v)Use Ok to test your code:
python3 ok -q insertOptional Questions
More trees practice
Q5: Same Shape
Write a function same_shape that returns True if two Trees have the same
shape. Two trees have the same shape if and only if they have the same number
of branches and each pair of corresponding children have the same shape.
def same_shape(t1, t2):
"""Returns whether two Trees t1, t2 have the same shape. Two trees have the
same shape iff they have the same number of branches and each pair
of corresponding branches have the same shape.
>>> t, s = Tree(1), Tree(3)
>>> same_shape(t, t)
True
>>> same_shape(t, s)
True
>>> t = Tree(1, [Tree(2), Tree(3)])
>>> same_shape(t, s)
False
>>> s = Tree(4, [Tree(3, [Tree(2, [Tree(1)])])])
>>> same_shape(t, s)
False
"""
"*** YOUR CODE HERE ***"
return len(t1.branches) == len(t2.branches) and \
all([same_shape(b1, b2) for b1, b2 in zip(t1.branches, t2.branches)])Use Ok to test your code:
python3 ok -q same_shapeQ6: Reverse Other
Write a function reverse_other that mutates the tree such that labels on
every other (odd-depth) level are reversed. For example,
Tree(1,[Tree(2, [Tree(4)]), Tree(3)]) becomes Tree(1,[Tree(3, [Tree(4)]), Tree(2)]).
Notice that the nodes themselves are not reversed; only the labels are.
def reverse_other(t):
"""Mutates the tree such that nodes on every other (odd-depth) level
have the labels of their branches all reversed.
>>> t = Tree(1, [Tree(2), Tree(3), Tree(4)])
>>> reverse_other(t)
>>> t
Tree(1, [Tree(4), Tree(3), Tree(2)])
>>> t = Tree(1, [Tree(2, [Tree(3, [Tree(4), Tree(5)]), Tree(6, [Tree(7)])]), Tree(8)])
>>> reverse_other(t)
>>> t
Tree(1, [Tree(8, [Tree(3, [Tree(5), Tree(4)]), Tree(6, [Tree(7)])]), Tree(2)])
"""
"*** YOUR CODE HERE ***"
def reverse_helper(t, need_reverse):
if t.is_leaf():
return
new_labs = [child.label for child in t.branches][::-1]
for i in range(len(t.branches)):
child = t.branches[i]
reverse_helper(child, not need_reverse)
if need_reverse:
child.label = new_labs[i]
reverse_helper(t, True)Use Ok to test your code:
python3 ok -q reverse_otherMore BSTs practice
Q7: Next Smallest Element
Write a function next_element that takes in a BST and a number N. It returns the
smallest element that is larger than N. For example, if you have this tree:
--8---
/ \
3- 10-
/ \ \
1 6 14
/ \ /
4 7 13 Then next_element(3) is 4, next_element(6) is 7,
and next_element(7) is 8.
def next_element(bst, n):
"""
This function takes in a BST and a number N and it returns the smallest
element that is greater than N, or None if it has no such element.
>>> t = BST(8, BST(3, BST(1), BST(6, BST(4), BST(7))), BST(10, BST.empty, BST(14, BST(13))))
>>> next_element(t, 1)
3
>>> next_element(t, 3)
4
>>> next_element(t, 5)
6
>>> next_element(t, 7)
8
>>> next_element(t, 10)
13
>>> next_element(t, 14)
>>> result = [1]
>>> a = next_element(t, 1)
>>> while a:
... result += [a]
... a = next_element(t, a)
>>> result
[1, 3, 4, 6, 7, 8, 10, 13, 14]
"""
"*** YOUR CODE HERE ***"
def next_or_default(t, n, default):
"""The smallest element in t greater than n, or default
if there is no such element."""
if t is BST.empty:
return default
elif t.label > n:
return next_or_default(t.left, n, t.label)
else:
return next_or_default(t.right, n, default)
return next_or_default(bst, n, None)Use Ok to test your code:
python3 ok -q next_element