Lab 5: Trees, Debugging, and Proj2 Prep
Due at 11:59pm on Friday, 07/12/2019.
Starter Files
Download lab05.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the Ok autograder.
Submission
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
Check that you have successfully submitted your code on
okpy.org.
Topics
Consult this section if you need a refresher on the material for this lab. It's okay to skip directly to the questions and refer back here should you get stuck.
Trees
A tree is a data structure that represents a hierarchy of information. A file system is a good example of a tree structure. For example, within your cs61a folder, you have folders separating your projects, lab assignments, and homework. The next level is folders that separate different assignments, hw01, lab01, hog, etc., and inside those are the files themselves, including the starter files and ok. Below is an incomplete diagram of what your cs61a directory might look like.
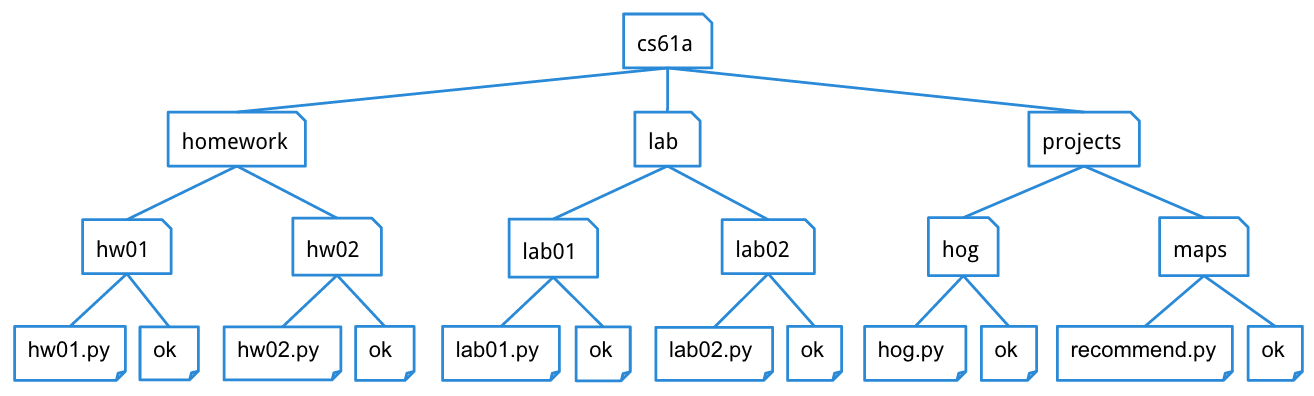
As you can see, unlike trees in nature, the tree abstract data type is drawn with the root at the top and the leaves at the bottom.
Some tree terminology:
- root: the node at the top of the tree
- label: the value in a node, selected by the
labelfunction - branches: a list of trees directly under the tree's root, selected by the
branchesfunction - leaf: a tree with zero branches
- node: any location within the tree (e.g., root node, leaf nodes, etc.)
Our tree abstract data type consists of a root and a list of its
branches. To create a tree and access its root value and branches, use the
following constructor and selectors:
Constructor
tree(label, branches=[]): creates a tree object with the givenlabelvalue at its root node and list ofbranches. Notice that the second argument to this constructor,branches, is optional - if you want to make a tree with no branches, leave this argument empty.
Selectors
label(tree): returns the value in the root node oftree.branches(tree): returns the list of branches of the giventree.
Convenience function
is_leaf(tree): returnsTrueiftree's list ofbranchesis empty, andFalseotherwise.
For example, the tree generated by
number_tree = tree(1,
[tree(2),
tree(3,
[tree(4),
tree(5)]),
tree(6,
[tree(7)])])would look like this:
1
/ | \
2 3 6
/ \ \
4 5 7To extract the number 3 from this tree, which is the label of the root of its second branch, we would do this:
label(branches(number_tree)[1])The print_tree function prints out a tree in a
human-readable form. The exact form follows the pattern illustrated
above, where the root is unindented, and each of its branches is
indented one level further.
def print_tree(t, indent=0):
"""Print a representation of this tree in which each node is
indented by two spaces times its depth from the root.
>>> print_tree(tree(1))
1
>>> print_tree(tree(1, [tree(2)]))
1
2
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> print_tree(numbers)
1
2
3
4
5
6
7
"""
print(' ' * indent + str(label(t)))
for b in branches(t):
print_tree(b, indent + 1)Required Questions
Q1: Merge
We've provided you with an implementation of the function merge.
merge takes 2 sorted lists lst1 and lst2, and returns a new list that contains all
the elements in the two lists in sorted order.
A list is sorted if the elements appear in nondecreasing order. [1, 2, 3] is a sorted list,
but [3, 1, 2] is not.
This solution does not pass the doctests. It is your job to figure out what is wrong with the implementation and correct the error.
Hint: if you're having trouble figuring out what's going on in the implemention, you might want to try the following:
- Use
printexpressions to debug. If you writeprint("DEBUG:", x), then you can print out the value of variablexwithout causing the ok tests to fail due to extra output. You should, of course, replacexwith whatever expression you want to print. - Come up with some additional doctests to understand the behavior of the function. You should not delete the doctests that are currently present, but you are free to add some of your own.
- Draw out an environment diagram for one of the doctests to see where the value of a variable differs from what you expect.
You are free to make any changes to the implementation as long as they do not fundamentally alter the approach (e.g. you should not convert the recursive solution to an iterative approach).
def merge(lst1, lst2):
"""Merges two sorted lists.
>>> merge([1], [2])
[1, 2]
>>> merge([2], [1])
[1, 2]
>>> merge([1, 3, 5], [2, 4, 6])
[1, 2, 3, 4, 5, 6]
>>> merge([5, 7], [2, 4, 6])
[2, 4, 5, 6, 7]
"""
if not lst1 or not lst2:
return []
return lst1 + lst2 elif lst1[0] < lst2[0]:
return [lst1[0]] + merge(lst1[1:], lst2)
else:
return [lst2[0]] + merge(lst1, lst2[1:])Use Ok to test your code:
python3 ok -q mergeQ2: Add Characters
Given two words, w1 and w2, we say w1 is a subsequence of w2
if all the letters in w1 appear in w2 in the same order (but
not necessarily all together). That is, you can add letters to any position in
w1 to get w2.
For example, "sing" is a substring of "absorbing" and "cat" is a substring of
"contrast".
Implement add_chars, which takes in w1 and w2, where w1 is a substring of w2. It should
return a string containing the characters you need to add to w1 to get w2. Your solution
must use recursion.
In the example above, you need to add the characters "aborb" to "sing" to get "absorbing", and you need to add "ontrs" to "cat" to get "contrast".
The letters in the string you return should be in the order you have to add them from left to right.
If there are multiple characters in the w2 that could correspond to characters in w1, use the
leftmost one. For example, add_words("coy", "cacophony") should return "acphon", not "caphon"
because the first "c" in "coy" corresponds to the first "c" in "cacophony".
def add_chars(w1, w2):
"""
Return a string containing the characters you need to add to w1 to get w2.
You may assume that w1 is a subsequence of w2.
>>> add_chars("owl", "howl")
'h'
>>> add_chars("want", "wanton")
'on'
>>> add_chars("rat", "radiate")
'diae'
>>> add_chars("a", "prepare")
'prepre'
>>> add_chars("resin", "recursion")
'curo'
>>> add_chars("fin", "effusion")
'efuso'
>>> add_chars("coy", "cacophony")
'acphon'
>>> from construct_check import check
>>> check(LAB_SOURCE_FILE, 'add_chars',
... ['For', 'While', 'Set', 'SetComp']) # Must use recursion
True
"""
"*** YOUR CODE HERE ***"
if not w1:
return w2
elif w1[0] == w2[0]:
return add_chars(w1[1:], w2[1:])
return w2[0] + add_chars(w1, w2[1:])Use Ok to test your code:
python3 ok -q add_charsQ3: Acorn Finder
The squirrels on campus need your help! There are a lot of trees on campus and
the squirrels would like to know which ones contain acorns. Define the function
acorn_finder, which takes in a tree and returns True if the tree contains a
node with the value 'acorn' and False otherwise.
def acorn_finder(t):
"""Returns True if t contains a node with the value 'acorn' and
False otherwise.
>>> scrat = tree('acorn')
>>> acorn_finder(scrat)
True
>>> sproul = tree('roots', [tree('branch1', [tree('leaf'), tree('acorn')]), tree('branch2')])
>>> acorn_finder(sproul)
True
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> acorn_finder(numbers)
False
>>> t = tree(1, [tree('acorn',[tree('not acorn')])])
>>> acorn_finder(t)
True
"""
"*** YOUR CODE HERE ***"
if label(t) == 'acorn':
return True
for b in branches(t):
if acorn_finder(b):
return True
return False
# Alternative solution
def acorn_finder(t):
if label(t) == 'acorn':
return True
return True in [acorn_finder(b) for b in branches(t)]Use Ok to test your code:
python3 ok -q acorn_finderOptional Questions
Shakespeare and Dictionaries
We will use dictionaries to approximate the entire works of Shakespeare! We're going to use a bigram language model. Here's the idea: We start with some word -- we'll use "The" as an example. Then we look through all of the texts of Shakespeare and for every instance of "The" we record the word that follows "The" and add it to a list, known as the successors of "The". Now suppose we've done this for every word Shakespeare has used, ever.
Let's go back to "The". Now, we randomly choose a word from this list, say "cat". Then we look up the successors of "cat" and randomly choose a word from that list, and we continue this process. This eventually will terminate in a period (".") and we will have generated a Shakespearean sentence!
The object that we'll be looking things up in is called a "successor table", although really it's just a dictionary. The keys in this dictionary are words, and the values are lists of successors to those words.
Q4: Successor Tables
Here's an incomplete definition of thebuild_successors_table
function. The input is a list of words (corresponding to a
Shakespearean text), and the output is a successors table. (By default,
the first word is a successor to "."). See the example below.
Note: there are two places where you need to write code, denoted by the two
"*** YOUR CODE HERE ***"
def build_successors_table(tokens):
"""Return a dictionary: keys are words; values are lists of successors.
>>> text = ['We', 'came', 'to', 'investigate', ',', 'catch', 'bad', 'guys', 'and', 'to', 'eat', 'pie', '.']
>>> table = build_successors_table(text)
>>> sorted(table)
[',', '.', 'We', 'and', 'bad', 'came', 'catch', 'eat', 'guys', 'investigate', 'pie', 'to']
>>> table['to']
['investigate', 'eat']
>>> table['pie']
['.']
>>> table['.']
['We']
"""
table = {}
prev = '.'
for word in tokens:
if prev not in table:
"*** YOUR CODE HERE ***"
table[prev] = [] "*** YOUR CODE HERE ***"
table[prev] += [word] prev = word
return tableUse Ok to test your code:
python3 ok -q build_successors_tableQ5: Construct the Sentence
Let's generate some sentences! Suppose we're given a starting word. We can look up this word in our table to find its list of successors, and then randomly select a word from this list to be the next word in the sentence. Then we just repeat until we reach some ending punctuation.
Hint: to randomly select from a list, import the Python random library with
import randomand use the expressionrandom.choice(my_list)
This might not be a bad time to play around with adding strings
together as well. Let's fill in the construct_sent function!
def construct_sent(word, table):
"""Prints a random sentence starting with word, sampling from
table.
>>> table = {'Wow': ['!'], 'Sentences': ['are'], 'are': ['cool'], 'cool': ['.']}
>>> construct_sent('Wow', table)
'Wow!'
>>> construct_sent('Sentences', table)
'Sentences are cool.'
"""
import random
result = ''
while word not in ['.', '!', '?']:
"*** YOUR CODE HERE ***"
result += word + ' '
word = random.choice(table[word]) return result.strip() + wordUse Ok to test your code:
python3 ok -q construct_sentPutting it all together
Great! Now let's try to run our functions with some actual data. The following snippet included in the skeleton code will return a list containing the words in all of the works of Shakespeare.
Warning: Do NOT try to print the return result of this function.
def shakespeare_tokens(path='shakespeare.txt', url='http://composingprograms.com/shakespeare.txt'):
"""Return the words of Shakespeare's plays as a list."""
import os
from urllib.request import urlopen
if os.path.exists(path):
return open('shakespeare.txt', encoding='ascii').read().split()
else:
shakespeare = urlopen(url)
return shakespeare.read().decode(encoding='ascii').split()Uncomment the following two lines to run the above function and build the successors table from those tokens.
# Uncomment the following two lines
# tokens = shakespeare_tokens()
# table = build_successors_table(tokens)Next, let's define a utility function that constructs sentences from this successors table:
>>> def sent():
... return construct_sent('The', table)
>>> sent()
" The plebeians have done us must be news-cramm'd."
>>> sent()
" The ravish'd thee , with the mercy of beauty!"
>>> sent()
" The bird of Tunis , or two white and plucker down with better ; that's God's sake."Notice that all the sentences start with the word "The". With a few
modifications, we can make our sentences start with a random word. The
following random_sent function (defined in your starter file) will
do the trick:
def random_sent():
import random
return construct_sent(random.choice(table['.']), table)Go ahead and load your file into Python (be sure to use the -i flag).
You can now call the random_sent function to generate random
Shakespearean sentences!
>>> random_sent()
' Long live by thy name , then , Dost thou more angel , good Master Deep-vow , And tak'st more ado but following her , my sight Of speaking false!'
>>> random_sent()
' Yes , why blame him , as is as I shall find a case , That plays at the public weal or the ghost.'More Trees Practice
Q6: Sprout leaves
Define a function sprout_leaves that takes in a tree, t, and a list of
values, vals. It produces a new tree that is identical to t, but where each
old leaf node has new branches, one for each value in vals.
For example, say we have the tree t = tree(1, [tree(2), tree(3, [tree(4)])]):
1
/ \
2 3
|
4If we call sprout_leaves(t, [5, 6]), the result is the following tree:
1
/ \
2 3
/ \ |
5 6 4
/ \
5 6def sprout_leaves(t, vals):
"""Sprout new leaves containing the data in vals at each leaf in
the original tree t and return the resulting tree.
>>> t1 = tree(1, [tree(2), tree(3)])
>>> print_tree(t1)
1
2
3
>>> new1 = sprout_leaves(t1, [4, 5])
>>> print_tree(new1)
1
2
4
5
3
4
5
>>> t2 = tree(1, [tree(2, [tree(3)])])
>>> print_tree(t2)
1
2
3
>>> new2 = sprout_leaves(t2, [6, 1, 2])
>>> print_tree(new2)
1
2
3
6
1
2
"""
"*** YOUR CODE HERE ***"
if is_leaf(t):
return tree(label(t), [tree(v) for v in vals])
return tree(label(t), [sprout_leaves(s, vals) for s in branches(t)])Use Ok to test your code:
python3 ok -q sprout_leavesQ7: Add trees
Define the function add_trees, which takes in two trees and returns a new
tree where each corresponding node from the first tree is added with the node
from the second tree. If a node at any particular position is present in one
tree but not the other, it should be present in the new tree as well.
Hint: You may want to use the built-in zip function to iterate over multiple sequences at once.
Note: If you feel that this one's a lot harder than the previous tree problems, that's totally fine! This is a pretty difficult problem, but you can do it! Talk about it with other students, and come back to it if you need to.
def add_trees(t1, t2):
"""
>>> numbers = tree(1,
... [tree(2,
... [tree(3),
... tree(4)]),
... tree(5,
... [tree(6,
... [tree(7)]),
... tree(8)])])
>>> print_tree(add_trees(numbers, numbers))
2
4
6
8
10
12
14
16
>>> print_tree(add_trees(tree(2), tree(3, [tree(4), tree(5)])))
5
4
5
>>> print_tree(add_trees(tree(2, [tree(3)]), tree(2, [tree(3), tree(4)])))
4
6
4
>>> print_tree(add_trees(tree(2, [tree(3, [tree(4), tree(5)])]), \
tree(2, [tree(3, [tree(4)]), tree(5)])))
4
6
8
5
5
"""
"*** YOUR CODE HERE ***"
if not t1:
return t2
if not t2:
return t1
new_label = label(t1) + label(t2)
t1_children, t2_children = branches(t1), branches(t2)
length_t1, length_t2 = len(t1_children), len(t2_children)
if length_t1 < length_t2:
t1_children += [None for _ in range(length_t1, length_t2)]
elif len(t1_children) > len(t2_children):
t2_children += [None for _ in range(length_t2, length_t1)]
return tree(new_label, [add_trees(child1, child2) for child1, child2 in zip(t1_children, t2_children)])Use Ok to test your code:
python3 ok -q add_trees