Lab 7: Midterm Review
Due at 11:59pm on Friday, 07/19/2019.
Starter Files
Download lab07.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the Ok autograder.
Submission
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
Check that you have successfully submitted your code on
okpy.org.
- In order to facilitate midterm studying, solutions to this lab were released with the lab. We encourage you to try out the problems and struggle for a while before looking at the solutions!
- Note: submitting this lab is entirely optional. It is not worth any credit, but will be helpful for your studying.
Required Questions
Functions
Q1: WWPD: Call Expressions
Use Ok to test your knowledge with the following "What Would Python Display?" questions:
python3 ok -q call_expressions -uFor all WWPD questions, type
Functionif you believe the answer is<function...>, >Errorif it errors, andNothingif nothing is displayed.
>>> from operator import add
>>> def double(x):
... return x + x
...
>>> def square(y):
... return y * y
...
>>> def f(z):
... add(square(double(z)), 1)
...
>>> f(4)
______# f(4) returns None, which is a special value that the interpreter hides unless explicitly printed>>> def foo(x, y):
... print("x or y")
... return x or y
...
>>> a = foo
______# We aren't calling foo here; we are just binding the variable a in the global frame to the function object foo
>>> b = foo()
______TypeError: foo() missing 2 required positional arguments: 'x' and 'y'
>>> c = a(print("x"), print("y"))
______x
y
x or y
>>> print(c)
______None>>> def welcome():
... print('welcome to')
... return 'hello'
...
>>> def cs61a():
... print('cs61a')
... return 'world'
...
>>> print(welcome(), cs61a())
______welcome to
cs61a
hello worldHigher Order Functions
Q2
Draw the environment diagram for the following code:
x = 5
def compose1(f, g):
def h(x):
return f(g(x))
return h
d = lambda y: y * x
x = 4
result = compose1(lambda z: z - 1, d)(3)There are 5 frames total (including the Global frame). In addition, consider the following questions:
- In frame
f1(the frame forcompose1), the parameterfpoints to a function object. What is the intrinsic name of that function object, and what frame is its parent? - In frame
f2, what name is the frame labeled with (hor λ)? Which frame is the parent off2? - In frame
f3, what name is the frame labeled with (f,g,d, or λ)? Which frame is the parent off3? In order to compute the return valuey * x, in which frame does Python findx? What is that value ofx? - In frame
f4, what name is the frame labeled with (f,g,d, or λ)? Which frame is the parent off3? - What value is the variable
resultbound to in the Global frame?
You can try out the environment diagram at tutor.cs61a.org.
- The intrinsic name of the function object that
fpoints to is λ (specifically, the lambda whose parameter isz). The parent frame of this lambda is Global. f2is labeled with the nameh; the parent frame off2isf1, since that is wherehis defined.f3is labeled with the name λ (specifically, it is the λ that takes in a parametery). The parent frame off3is Global, since that is where this lambda was defined (the lined = lambda y: y * x).f4is labeled with the name λ (specifically, it is the λ that takes a parameterz). The parent frame off4is Global, since that is where the lambda is defined.You might think that the parent of
f4isf1, sincelambda z: z - 1is being passed intocompose1. Remember, however, that operands are evaluated before the operator is applied (that is, before we create the framef1). Since we are evaluatinglambda z: z - 1in the Global frame, its parent is Global.- The variable
resultis bound to 11.
Recursion & Tree Recursion
Q3: Insect Combinatorics
Consider an insect in an M by N grid. The insect starts at the
bottom left corner, (0, 0), and wants to end up at the top right
corner, (M-1, N-1). The insect is only capable of moving right or
up. Write a function paths that takes a grid length and width
and returns the number of different paths the insect can take from the
start to the goal. (There is a closed-form solution to this problem,
but try to answer it procedurally using recursion.)
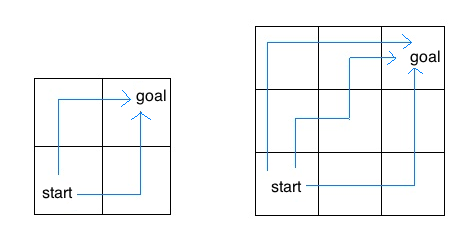
For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
if m == 1 or n == 1:
return 1
return paths(m - 1, n) + paths(m, n - 1)Use Ok to test your code:
python3 ok -q pathsQ4: Number of Trees
How many different possible full binary tree (each node has two branches or 0, but never 1) structures exist that have exactly n leaves?
For those interested in combinatorics, this problem does have a closed form solution):
def num_trees(n):
"""How many full binary trees have exactly n leaves? E.g.,
1 2 3 3 ...
* * * *
/ \ / \ / \
* * * * * *
/ \ / \
* * * *
>>> num_trees(1)
1
>>> num_trees(2)
1
>>> num_trees(3)
2
>>> num_trees(8)
429
"""
"*** YOUR CODE HERE ***"
if n == 1:
return 1
return sum(num_trees(k) * num_trees(n-k) for k in range(1, n))Use Ok to test your code:
python3 ok -q num_treesTree Practice
Q5: Pruning Leaves
Define a function prune_leaves that given a tree t and a tuple of values
vals, produces a version of t with all its leaves that are in vals
removed. Do not attempt to try to remove non-leaf nodes and do not remove
leaves that do not match any of the items in vals. Return None if pruning
the tree results in there being no nodes left in the tree.
def prune_leaves(t, vals):
"""Return a modified copy of t with all leaves that have a label
that appears in vals removed. Return None if the entire tree is
pruned away.
>>> t = tree(2)
>>> print(prune_leaves(t, (1, 2)))
None
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> print_tree(numbers)
1
2
3
4
5
6
7
>>> print_tree(prune_leaves(numbers, (3, 4, 6, 7)))
1
2
3
5
6
"""
"*** YOUR CODE HERE ***"
if is_leaf(t) and (label(t) in vals):
return None
new_branches = []
for b in branches(t):
new_branch = prune_leaves(b, vals)
if new_branch:
new_branches += [new_branch]
return tree(label(t), new_branches)Use Ok to test your code:
python3 ok -q prune_leavesSequences and Mutability
Q6: WWPD: Mutability?
What would Python display? Try to figure it out before you type it into the interpreter!
Use Ok to test your knowledge with the following "What Would Python Display?" questions:
python3 ok -q mutability -u
>>> lst = [5, 6, 7, 8]
>>> lst.append(6)
______Nothing
>>> lst
______[5, 6, 7, 8, 6]
>>> lst.insert(0, 9)
>>> lst
______[9, 5, 6, 7, 8, 6]
>>> x = lst.pop(2)
>>> lst
______[9, 5, 7, 8, 6]
>>> lst.remove(x)
>>> lst
______[9, 5, 7, 8]
>>> a, b = lst, lst[:]
>>> a is lst
______True
>>> b == lst
______True
>>> b is lst
______False>>> pokemon = {'pikachu': 25, 'dragonair': 148, 'mew': 151}
>>> pokemon['pikachu']
______25
>>> len(pokemon)
______3
>>> pokemon['jolteon'] = 135
>>> pokemon['mew'] = 25
>>> len(pokemon)
______4
>>> 'mewtwo' in pokemon
______False
>>> 'pikachu' in pokemon
______True
>>> 25 in pokemon
______False
>>> 151 in pokemon
______False
>>> pokemon['ditto'] = pokemon['jolteon']
>>> pokemon['ditto']
______135Q7: Dict to List
Fill in the blanks in the code to complete the implementation of the
dict_to_lst function, which takes in a dictionary d and returns a list.
The resulting list should contain all the (key, value) pairs in the input
dictionary as two-element tuples, where the pairs with smaller values come
first.
Note: The
.items()method returns a collection of (key, value) pairs for a dictionary:>>> for pair in {1: 2, 3: 4, 5: 6}.items(): ... print(pair) (1, 2) (3, 4) (5, 6)
def dict_to_lst(d):
"""Returns a list containing all the (key, value) pairs in d as two-element
tuples ordered by increasing value.
>>> nums = {1: 5, 2: 3, 3: 4}
>>> dict_to_lst(nums)
[(2, 3), (3, 4), (1, 5)]
>>> words = {'first': 'yes', 'second': 'no', 'third': 'perhaps'}
>>> dict_to_lst(words)
[('second', 'no'), ('third', 'perhaps'), ('first', 'yes')]
"""
result = []
for _ in range(len(d)):
pair = min(d.items(), key=______________________)
pair = min(d.items(), key=lambda item: item[1]) d.pop(_________)
d.pop(pair[0]) _______________________
result.append(pair) return result
# Alternate solution
# This solution is the ideal way to solve this problem, but we haven't learned
# how to use the sorted function so don't worry if you don't understand it.
def dict_to_list2(d):
return sorted(d.items(), key=lambda pair: pair[1])Use Ok to test your code:
python3 ok -q dict_to_lst