Let's imagine you order a mushroom and cheese pizza from La Val's, and that they represent your order as a list:

>>> pizza = ['cheese', 'mushrooms']

A couple minutes later, you realize that you really want onions on the pizza. Based on what we know so far, La Val's would have to build an entirely new list to add onions:

>>> pizza = ['cheese', mushrooms']
>>> new_pizza = pizza + ['onions'] # creates a new python list
>>> new_pizza
['cheese', mushrooms', 'onions']
>>> pizza # the original list is unmodified
['cheese', 'mushrooms']

This is silly, considering that all La Val's had to do was add onions on top of pizza instead of making an entirely new pizza.

We can fix this issue with list mutation. In Python, some objects, such as lists and dictionaries, are mutable, meaning that their contents or state can be changed over the course of program execution. Other objects, such as numeric types, tuples, and strings, are immutable, meaning they cannot be changed once they are created.

Therefore, instead of building a new pizza, we can just mutate pizza to add some onions!

>>> pizza.append('onions')
>>> pizza
['cheese', 'mushrooms', 'onions']

append is what's known as a method, or a function that belongs to an object, so we have to call it using dot notation. We'll talk more about methods later in the course, but for now, here's a list of useful list mutation methods:

• append(el): Adds el to the end of the list, and returns None
• extend(lst): Extends the list by concatenating it with lst, and returns None
• insert(i, el): Insert el at index i (does not replaceelement but adds a new one), and returns None
• remove(el): Removes the first occurrence of el in list, otherwise errors, and returns None
• pop(i): Removes and returns the element at index i

We can also use the familiar indexing operator with an assignment statement to change an existing element in a list. For example, we can change the element at index 1 and to 'tomatoes' like so:

>>> pizza[1] = 'tomatoes'
>>> pizza
['cheese', 'tomatoes', 'onions']

Questions

Q1: WWPD

>>> s1 = [1, 2, 3]
>>> s2 = s1
>>> s1 is s2

>>> s2.extend([5, 6])
>>> s1[4]

>>> s1.append([-1, 0, 1])
>>> s2[5]

>>> s3 = s2[:]
>>> s3.insert(3, s2.pop(3))
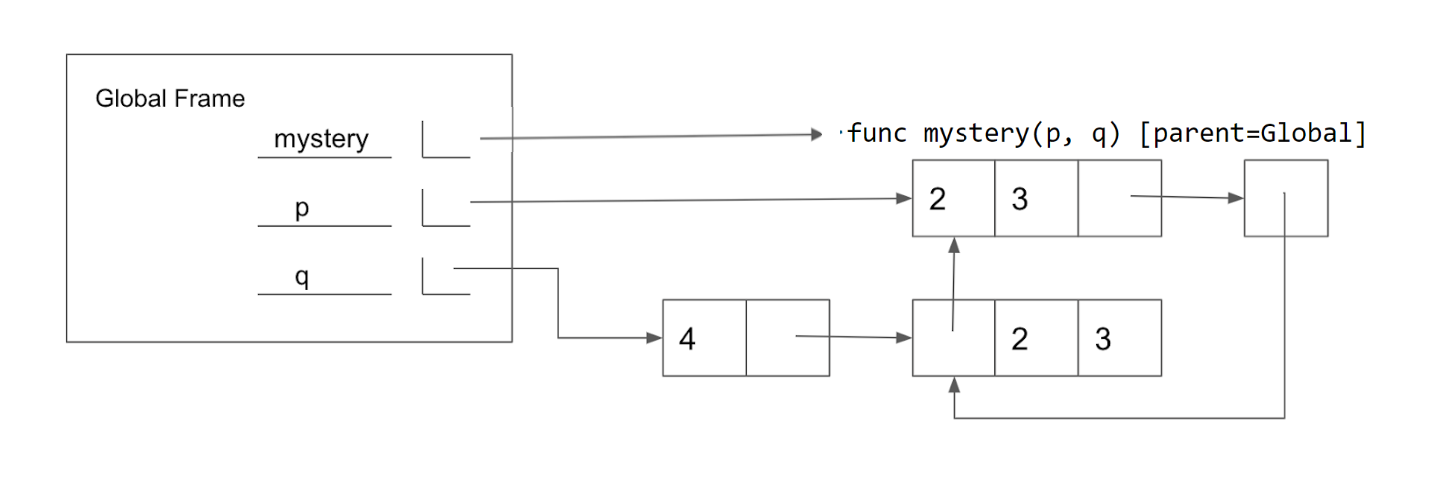
>>> len(s1)

>>> s1[4] is s3[6]

>>> s3[s2[4][1]]

>>> s1[:3] is s2[:3]

>>> s1[:3] == s2[:3]

Q2: (Optional) Mystery Reverse Environment Diagram

Fill in the lines below so that the variables in the global frame are bound to the values below. Note that the image does not contain a full environment diagram. You may only use brackets, commas, colons, p and q in your answer.

Q3: Add This Many

Write a function that takes in a valuex, a value el, and a list s and adds as many el's to the end of the list as there are x's. Make sure to modify the original list using list mutation techniques.

Q4: Insert Items

Write a function which takes in a list lst, an argument entry, and another argument elem. This function will check through each item in lst to see if it is equal to entry. Upon finding an item equivalent to entry, the function should modify the list by placing elem into lst right after the item. At the end of the function, the modified list should be returned.

See the doctests for examples on how this function is utilized. Use list mutation to modify the original list, no new lists should be created or returned.

Be careful in situations where the values passed into entry and elem are equivalent, so as not to create an infinitely long list while iterating through it. If you find that your code is taking more than a few seconds to run, it is most likely that the function is in a loop of inserting new values.

Trees

In computer science, trees are recursive data structures that are widely used in various settings. The diagram below is an example of a tree.

Notice that the tree branches downward. In computer science, the root of a tree starts at the top, and the leaves are at the bottom.

Some terminology regarding trees:

• Parent Node: A node that has branches. Parent nodes can have multiple branches.
• Child Node: A node that has a parent. A child node can only belong to one parent.
• Root: The top node of the tree. In our example, the node that contains 1 is the root.
• Label: The value at a node. In our example, all of the integers are values.
• Leaf: A node that has no branches. In our example, the nodes that contain 4, 5, 6, and 2 are leaves.
• Branch: A subtree of the root. Note that trees have branches, which are trees themselves: this is why trees are recursive data structures.
• Depth: How far away a node is from the root. In other words, the number of edges between the root of the tree to the node. In the diagram, the node containing 3 has depth 1; the node containing 4 has depth 2. Since there are no edges between the root of the tree and itself, the depth of the root is 0.
• Height: The depth of the lowest leaf. In the diagram, the nodes containing 4, 5, and 6 are all the lowest leaves, and they have depth 2. Thus, the entire tree has height 2.

In computer science, there are many different types of trees. Some vary in the number of branches each node has; others vary in the structure of the tree.

Trees Implementation

A tree has both a value for the root node and a sequence of branches, which are also trees. In our implementation, we represent the branches as a list of trees. Since a tree is an abstract data type, our choice to use lists is just an implementation detail.

• The arguments to the constructor tree are the value for the root node and an optional list of branches. If no branches parameter is provided, the default value [] is used.
• The selectors for these are label and branches.

Remember branches returns a list of trees and not a tree directly. It's important to distinguish between working with a tree and working with a list of trees.

We have also provided a convenience function, is_leaf.

Let's try to create the tree below.

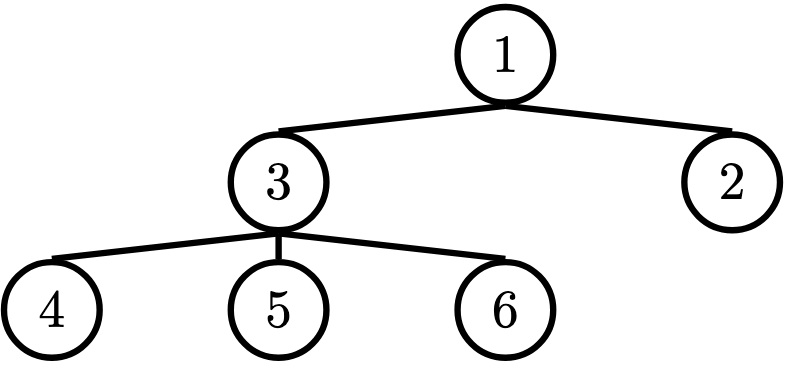
# Example tree construction
t = tree(1,
      [tree(3,
          [tree(4),
           tree(5),
           tree(6)]),
      tree(2)])

Questions

Q5: (Warmup) Height

Q6: Maximum Path Sum

Write a function that takes in a tree and returns the maximum sum of the values along any path in the tree. Recall that a path is from the tree's root to any leaf.

Q7: Find Path

Write a function that takes in a tree and a value x and returns a list containing the nodes along the path required to get from the root of the tree to a node containing x.

If x is not present in the tree, return None. Assume that the entries of the tree are unique.

For the following tree, find_path(t, 5) should return [2, 7, 6, 5]

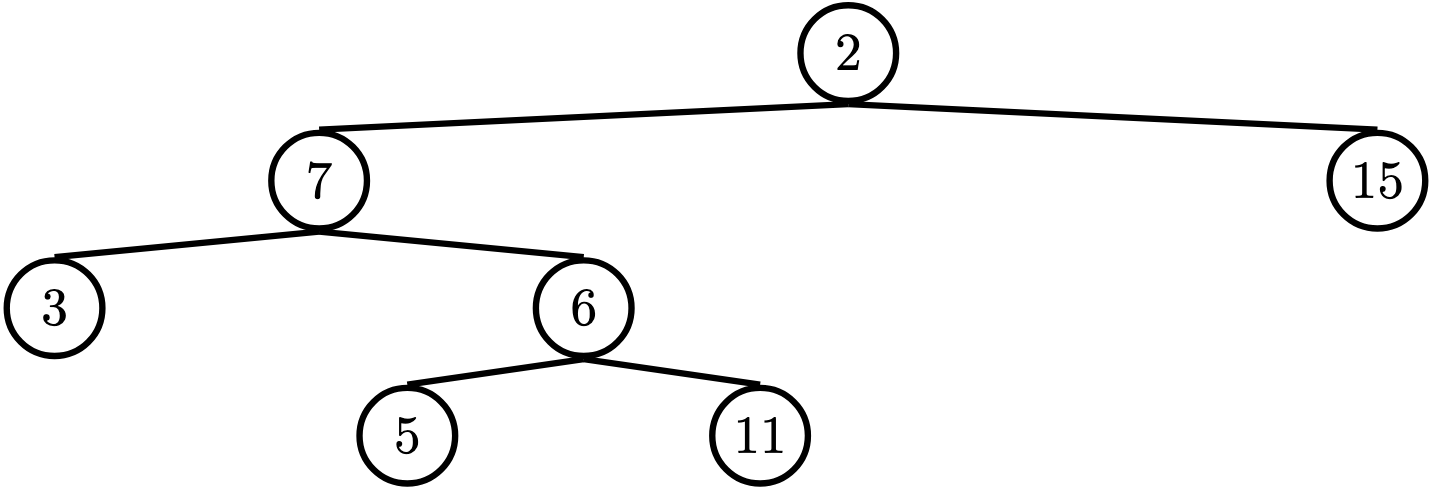
Exam Prep

Q8: Perfectly Balanced and Pruned

Difficulty: ⭐

Part A: Implement sum_tree, which takes adds together all the labels in a tree.

Part B: Implement balanced, a function which takes in a tree and returns whether each of the branches have the same total sum, and each branch is balanced.

Part C: Implement prune_tree, a function which takes in a tree t as well as a function predicate that returns True or False for each label of each tree node. prune_tree returns a new tree where any node for which predicate of the label of that node returns True, then all the branches for that tree are pruned (not included in the new tree).

IMPORTANT: You may use as many lines as you want for these two parts.

Challenge: Solve both of these parts with just 1 line of code each.

Q9: Closest - Spring 2015 Midterm 2 Q3(c)

IMPORTANT: For this problem, you will be given time during the Exam Prep section to solve on your own before we go over it.

Difficulty: ⭐⭐

Implement closest, which takes a tree of numbers t and returns the smallest absolute difference anywhere in the tree between an entry and the sum of the entries of its branches. The sum only compares the any node value to the sum of its branches, or nodes one level below that node.

The built-in min function takes a sequence and returns its minimum value.

Reminder: A branch of a branch of a tree t is not considered to be a branch of t.

Q10: Recursion on Tree ADT - Summer 2014 Midterm 1 Q7

Difficulty: ⭐⭐

Define a function dejavu, which takes in a tree of numbers t and a number n. It returns True if there is a path from the root to a leaf such that the sum of the numbers along that path is n and False otherwise.

IMPORTANT: For this problem, the starter code template is just a suggestion. You are welcome to add/delete/modify the starter code template, or even write your own solution that doesn’t use the starter code at all.

Use Ok to test your code:

python3 ok -q dejavu

"""
>>> my_tree = tree(2, [tree(3, [tree(5), tree(7)]), tree(4)])
>>> dejavu(my_tree, 12) # 2 -> 3 -> 7
True
>>> dejavu(my_tree, 5) # Sums of partial paths like 2 -> 3 don ’t count
False
"""
if is_leaf(t):
    return ____________________________
for ____________________________:
    if ____________________________:
        return ____________________________
return False

"""Construct a tree with the given label value and a list of branches."""
for branch in branches:
    assert is_tree(branch), 'branches must be trees'
return [label] + list(branches)

"""Return the label value of a tree."""
return tree[0]

"""Return the list of branches of the given tree."""
return tree[1:]

"""Returns True if the given tree is a tree, and False otherwise."""
if type(tree) != list or len(tree) < 1:
    return False
for branch in branches(tree):
    if not is_tree(branch):
        return False
return True

"""Returns True if the given tree's list of branches is empty, and False
otherwise.
"""
return not branches(tree)

"""Print a representation of this tree in which each node is
indented by two spaces times its depth from the root.

>>> print_tree(tree(1))
1
>>> print_tree(tree(1, [tree(2)]))
1
  2
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> print_tree(numbers)
1
  2
  3
    4
    5
  6
    7
"""
print('  ' * indent + str(label(t)))
for b in branches(t):
    print_tree(b, indent + 1)

"""Returns a copy of t. Only for testing purposes.

>>> t = tree(5)
>>> copy = copy_tree(t)
>>> t = tree(6)
>>> print_tree(copy)
5
"""
return tree(label(t), [copy_tree(b) for b in branches(t)])

Q11: Forest Path - Fall 2015 Final Q3 (a)(b)(d)

Difficulty: ⭐⭐⭐

Definition: A path through a tree is a list of adjacent node values that starts with the root value and ends with a leaf value. For example, the paths of tree(1, [tree(2), tree(3, [tree(4), tree(5)])]) are

[1, 2]
[1, 3, 4]
[1, 3, 5]

Part A: Implement bigpath, which takes a tree t and an integer n. It returns the number of paths in t whose sum is at least n. Assume that all node values of t are integers.

Part B: Implement allpath which takes a tree t, a one-argument predicate f, a two-argument reducing function g, and a starting value s. It returns the number of paths p in t for which f(reduce(g, p, s)) returns a truthy value. The reduce function is in the code. Pay close attention to the order of arguments to the f function in reduce. You do not need to call it, though.

Part C: Re-implement bigpath (Part A) using allpath (Part B). Assume allpath is implemented correctly.

Q12: Extra Practice

Difficulty: >⭐⭐⭐

Fall 2020 Exam Prep on Trees