Discussion 8: Linked Lists, Mutable Trees, String Representation

• disc08.pdf

This is an online worksheet that you can work on during discussions. Your work is not graded and you do not need to submit anything. The last section of most worksheets is Exam Prep, which will typically only be taught by your TA if you are in an Exam Prep section. You are of course more than welcome to work on Exam Prep problems on your own.

Representation - Repr and Str

There are two main ways to produce the "string" of an object in Python: str() and repr(). While the two are similar, they are used for different purposes. str() is used to describe the object to the end user in a "Human-readable" form, while repr() can be thought of as a "Computer-readable" form mainly used for debugging and development.

When we define a class in Python, str() and repr() are both built-in methods for the class. We can call an object's str() and repr() by using their respective methods. These methods can be invoked by calling repr(obj) or str(obj) rather than the dot notation format obj.__repr__() or obj.__str__(). In addition, the print() function calls the str() method of the object, while simply calling the object in interactive mode calls the repr() method.

Here's an example:

class Rational:
    def __init__(self, numerator, denominator):
        self.numerator = numerator
        self.denominator = denominator
    def __str__(self):
        return f'{self.numerator}/{self.denominator}'
    def __repr__(self):
        return f'Rational({self.numerator},{self.denominator})'

>>> a = Rational(1, 2)
>>> str(a)
'1/2'
>>> repr(a)
'Rational(1,2)'
>>> print(a)
1/2
>>> a
Rational(1,2)

Questions

Q1: Repr-esentation WWPD

What would Python display?

class A:
    def __init__(self, x):
        self.x = x
    def __repr__(self):
         return self.x
    def __str__(self):
         return self.x * 2

class B:
    def __init__(self):
         print('boo!')
         self.a = []
    def add_a(self, a):
         self.a.append(a)
    def __repr__(self):
         print(len(self.a))
         ret = ''
         for a in self.a:
             ret += str(a)
         return ret

>>> A('one')

Your Answer:

>>> print(A('one'))

Your Answer:

>>> repr(A('two'))

Your Answer:

>>> b = B()

Your Answer:

>>> b.add_a(A('a'))
>>> b.add_a(A('b'))
>>> b

Your Answer: Your Answer:

Linked Lists

There are many different implementations of sequences in Python. Today, we'll explore the linked list implementation.

A linked list is either an empty linked list, or a Link object containing a first value and the rest of the linked list.

To check if a linked list is an empty linked list, compare it against the class attribute Link.empty:

if link is Link.empty:
    print('This linked list is empty!')
else:
    print('This linked list is not empty!')

Check out the implementation of the Link class below:

class Link:
    empty = ()
    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest:
            rest_str = ', ' + repr(self.rest)
        else:
            rest_str = ''
        return 'Link({0}{1})'.format(repr(self.first), rest_str)

    def __str__(self):
        string = '<'
        while self.rest is not Link.empty:
            string += str(self.first) + ' '
            self = self.rest
        return string + str(self.first) + '>'

Questions

Q2: The Hy-rules of Linked Lists

In this question, we are given the following Linked List:

ganondorf = Link('zelda', Link('young link', Link('sheik', Link.empty)))

What expression would give us the value 'sheik' from this Linked List?

Your Answer:

What is the value of ganondorf.rest.first?

Your Answer:

Q3: Sum Nums

Write a function that takes in a linked list and returns the sum of all its elements. You may assume all elements in s are integers. Try to implement this recursively!

Run in 61A Code

Q4: Multiply Lnks

Write a function that takes in a Python list of linked lists and multiplies them element-wise. It should return a new linked list.

If not all of the Link objects are of equal length, return a linked list whose length is that of the shortest linked list given. You may assume the Link objects are shallow linked lists, and that lst_of_lnks contains at least one linked list.

Run in 61A Code

Q5: Flip Two

Write a recursive function flip_two that takes as input a linked list s and mutates s so that every pair is flipped.

Run in 61A Code

Trees

Recall the tree abstract data type: a tree is defined as having a label and some branches. Previously, we implemented the tree abstraction using Python lists. Let's look at another implementation using objects instead:

class Tree:
    def __init__(self, label, branches=[]):
        for b in branches:
            assert isinstance(b, Tree)
        self.label = label
        self.branches = branches

    def is_leaf(self):
        return not self.branches

With this implementation, we can mutate a tree using attribute assignment, which wasn't possible in the previous implementation using lists. That's why we sometimes call these objects "mutable trees."

>>> t = Tree(3, [Tree(4), Tree(5)])
>>> t.label = 5
>>> t.label
5

Questions

Q6: Make Even

Define a function make_even which takes in a tree t whose values are integers, and mutates the tree such that all the odd integers are increased by 1 and all the even integers remain the same. Run in 61A Code

Q7: Leaves

Write a function leaves that returns a list of all the label values of the leaf nodes of a Tree.

Run in 61A Code

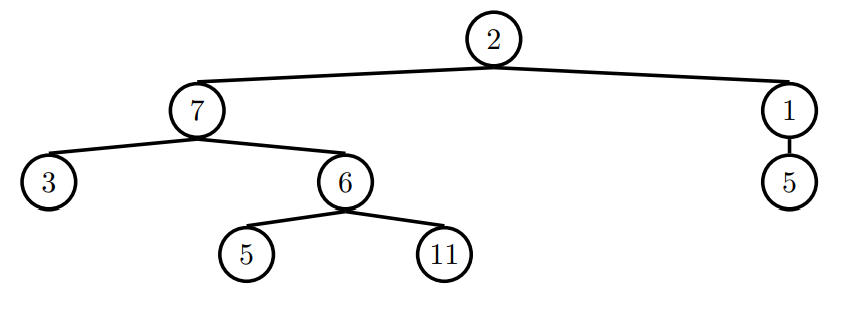
Q8: Find Paths

**Hint**: This question is similar to find_paths on Discussion 05.

Define the procedure find_paths that, given a Tree t and an entry, returns a list of lists containing the nodes along each path from the root of t to entry. You may return the paths in any order.

For instance, for the following tree tree_ex, find_paths should behave as specified in the function doctests.

Run in 61A Code

Exam prep

Q9: Node Printer

Difficulty: ⭐⭐_

Your friend wants to print out all of the values in some trees. Based on your experience in CS 61A, you decide to come up with an unnecessarily complicated solution. You will provide them with a function that takes in a tree and returns a node-printing function. When you call a node-printing function, it prints out the label of one node in the tree. Each time you call the function it will print the label of a different node. You may assume that your friend is polite and will not call your function after printing out all of the tree's node labels. You may print the labels in any order, so long as you print the label of each node exactly once.

(Very) optional challenge: See if you can come up with a solution that prints out all of the nodes from one layer before moving on to the next (hint: it still fits within the skeleton code).

Important: The skeleton code is only a suggestion; feel free to add or remove lines as you see fit. Also, it's okay if your code doesn't pass the doctest; if you run the test case with the green arrow and all 8 values are printed exactly once, then your implementation is fine.

Run in 61A Code

Q10: Iterator Tree Link Tree Iterator

Difficulty: ⭐⭐

Part A: Fill out the function funcs, which is a generator that takes in a linked list link and yields functions.

The linked list link defines a path from the root of the tree to one of its nodes, with each element of link specifying which branch to take by index. Applying all functions sequentially to a Tree instance will evaluate to the label of the node at the end of the specified path.

For example, using the Tree t defined in the code, funcs(Link(2)) yields 2 functions. The first gets the third branch from t -- the branch at index 2 -- and the second function gets the label of this branch.

>>> func_generator = funcs(Link(2)) # get label of third branch
>>> f1 = next(func_generator)
>>> f2 = next(func_generator)
>>> f2(f1(t))
4

Part B: Using funcs from above, fill out the definition for apply, which applies g to the element in t who's position is at the end of the path defined by link.

Run in 61A Code

Q11: O!-Pascal - Fall 2017 Final Q4

Difficulty: ⭐⭐

Pasal's Triangle is perhaps familiar to you from the diagram below, which shows the first five rows.

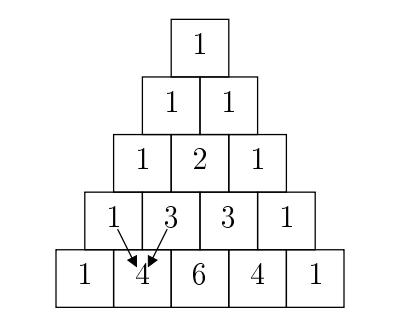
Every square is the sum of the two squares above it (as illustrated by the arrows showing here the value 4 comes from), unless it doesn't have two squares above it, in whih case its value is 1.

(a) Given a linked list that represents a row in Pasal's triangle, return a linked list that will represent the row below it. Your solution must not use L.getitem(k) (or L[k]). You may not need all the lines.

(b) Fill in the procedure called makepascaltriangle to create a full Pacsal Triangle of height k. Represent the entire triangle as a linked list of the rows of the triangles, whih are also linked lists. Again, your solution must not use L.getitem(k) method (or L[k]).

(c) Pascal's Triangle contains many patterns within it. For instance, consider the diagonals. The first diagonal (going down the left side) is just a series of 1s. The seond diagonal (consisting of the second elements of each row) is the counting numbers. The third diagonal is the triangular numbers. Fill in the procedure called diagonal to take in a Pascal Triangle (represented by a linked list from part b) and return a linked list containing the indicated diagonal. As before, your solution must not use L.getitem(k) (or L[k]), and you may not need all the lines.

Run in 61A Code

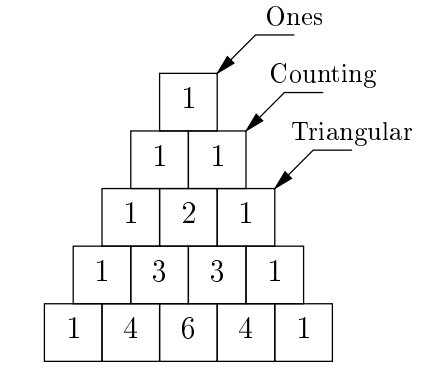
(d) Cirle the Θ expression that desribes the number of integers contained in the value of the expression make pascal triangle(n). Θ(1) Θ(log n) Θ(n) Θ(n²) Θ(2ⁿ) None of these