Discussion 9: Scheme, Scheme Lists

• disc09.pdf

This is an online worksheet that you can work on during discussions. Your work is not graded and you do not need to submit anything. The last section of most worksheets is Exam Prep, which will typically only be taught by your TA if you are in an Exam Prep section. You are of course more than welcome to work on Exam Prep problems on your own.

Introduction

In the next part of the course, we will be working with the Scheme programming language. In addition to learning how to write Scheme programs, we will eventually write a Scheme interpreter in Project 4!

Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses a prefix notation and (often many) nested parentheses (see http://xkcd.com/297/). Scheme features first-class functions and optimized tail-recursion, which were relatively new features at the time.

Primitives and Defining Variables

Scheme has a set of atomic primitive expressions. Atomic means that these expressions cannot be divided up.

scm> 123
123
scm> #t
True
scm> #f
False

Unlike in Python, the only primitive in Scheme that is a false value is #f and its equivalents, false and False. This means that 0 is not false.

The define special form defines variables and procedures by binding a value to a variable, just like the assignment statement in Python. When a variable is defined, the define special form returns a symbol of its name. A procedure is what we call a function in Scheme.

The syntax to define a variable and procedure are:

• (define <variable name> <value>)
• (define (<function name> <parameters>) <function body>))

Special forms are types of expressions with unique evaluation rules that can do a variety of things. Often times, speical forms are analagous to statements in Python, such as assignment statements, if statements, and def statements. However, all special forms in Scheme evaluate to a value. We'll learn more about special forms later in the discussion.

Questions

scm> (define a 1)

Your Answer:

scm> a

Your Answer:

scm> (define b a)

Your Answer:

scm> b

Your Answer:

scm> (define c 'a)

Your Answer:

scm> c

Your Answer:

Call Expressions

Call expressions apply a procedure to some arguments.

(<operator> <operand1> <operand2> ...)

Call expressions in Scheme work exactly like they do in Python. To evaluate them:

1. Evaluate the operator to get a procedure.
2. Evaluate each of the operands from left to right.
3. Apply the value of the operator to the evaluated operands.

For example, consider the call expression (+ 1 2). First, we evaluate the symbol + to get the built-in addition procedure. Then we evaluate the two operands 1 and 2 to get their corresponding atomic values. Finally, we apply the addition procedure to the values 1 and 2 to get the return value 3.

Operators may be symbols, such as + and *, or more complex expressions, as long as they evaluate to procedure values.

scm> (- 1 1)                 ; 1 - 1
0
scm> (/ 8 4 2)               ; 8 / 4 / 2
1
scm> (* (+ 1 2) (+ 1 2))     ; (1 + 2) * (1 + 2)
9

Some important built-in functions you'll want to know are:

• +, -, *, /
• =, >, >=, <, <=
• quotient, modulo, even?, odd?, null?

Questions

What would Scheme display? As a reminder, the built-in quotient function performs floor division.

scm> (define a (+ 1 2))

Your Answer:

scm> a

Your Answer:

scm> (define b (- (+ (* 3 3) 2) 1))

Your Answer:

scm> (+ a b)

Your Answer:

scm> (= (modulo b a) (quotient 5 3))

Your Answer:

Special Forms

Special form expressions contain a special form as the operator. Special form expressions do not follow the same rules of evaluation as call expressions. Each special form has its own rules of evaluation -- that's what makes them special!

If Expression

An if expression looks like this:

(if <predicate> <if-true> [if-false])

<predicate> and <if-true> are required expressions and [if-false] is optional.

The rules for evaluation are as follows:

1. Evaluate <predicate>.
2. If <predicate> evaluates to a truth-y value, evaluate <if-true> and return its value. Otherwise, evaluate [if-false] if provided and return its value.

This is a special form because not all operands will be evaluated! Only one of the second and third operands is evaluated, depending on the value of the first operand.

Remember that only #f is a false-y value in Scheme; everything else is truth-y.

scm> (if (< 4 5) 1 2)
1
scm> (if #f (/ 1 0) 42)
42

Boolean operators

Like Python, Scheme also has the boolean operators and, or, and not. and and or are special forms because they are short-circuiting operators.

• and takes in any amount of operands and evaluates these operands from left to right until one evaluates to a false-y value. It returns that first false-y value. If there are no false-y values, it returns the value of the last expression (or #t if there are no operands)
• or also evaluates any number of operands from left to right until one evaluates to a truth-y value. It returns that first truth-y value. If there are no truth-y values, it returns the value of the last expression (or #f if there are no operands)
• not takes in a single operand, evaluates it, and returns its opposite truthiness value. Note that not is a regular procedure and not a special form.

Important note: the only false-y value in scheme is #f. In particular, 0 is truth-y!

scm> (and 25 32)
32
scm> (or 1 (/ 1 0))    ; Short-circuits
1
scm> (not (odd? 10))
#t

Questions

What would Scheme display?

scm> (if (or #t (/ 1 0)) 1 (/ 1 0))

Your Answer:

scm> ((if (< 4 3) + -) 4 100)

Your Answer:

Lambdas and Defining Functions

All Scheme procedures are lambda procedures. One way to create a procedure is to use the lambda special form.

(lambda (<param1> <param2> ...) <body>)

This expression creates a lambda function with the given parameters and body, but does not evaluate the body. Just like in Python, the body is not evaluated until the function is called and applied to some argument values. The fact that neither operand is evaluated is what makes lambda a special form.

Another similarity to Python is that lambda expressions do not assign the returned function to any name. We can assign the value of an expression to a name with a define special form.

For example, (define square (lambda (x) (* x x))) creates a lambda procedure that squares its argument and assigns that procedure to the name square.

The second version of the define special form is a shorthand for this function definition:

(define (<name> <param1> <param2 ...>) <body>)

This expression creates a function with the given parameters and body and binds it to the given name.

scm> (define square (lambda (x) (* x x))) ; Bind the lambda function to the name square
square
scm> (define (square x) (* x x))          ; Equivalent to the line above
square
scm> square
(lambda (x) (* x x))
scm> (square 4)
16

Questions

Q1: Factorial

Write a function that returns the factorial of a number.

Run in 61A Code

Q2: Fibonacci

Write a function that returns the n-th Fibonacci number.

Run in 61A Code

scm> (fib 0)
0
scm> (fib 1)
1
scm> (fib 10)
55

Pairs and Lists

All lists in Scheme are linked lists. Scheme lists are composed of two element pairs. We define a list as being either

• the empty list, nil
• a pair whose second element is a list

As in Python, linked lists are recursive data structures. The base case is the empty list.

We use the following procedures to construct and select from lists:

• (cons first rest) constructs a list with the given first element and rest of the list. For now, if rest is not a pair or nil it will error.
• (car lst) gets the first item of the list
• (cdr lst) gets the rest of the list

To visualize Scheme lists, you can use the draw function in code.cs61a.org. The list from the example below is loaded here.

scm> nil
()
scm> (define lst (cons 1 (cons 2 (cons 3 nil))))
lst
scm> lst
(1 2 3)
scm> (car lst)
1
scm> (cdr lst)
(2 3)
scm> (car (cdr lst))
2
scm> (cdr (cdr (cdr lst)))
()

The rule for displaying lists is very similar to that for the Link class from earlier in the class's __str__ method. It prints out the elements in the linked list as if the list has no nested structure. The only difference is that Link.__str__ uses angle brackets <> and scheme uses parentheses ().

Try drawing out the lists below yourself, then check your answer.

scm> (cons 1 (cons 2 (cons 3 nil)))
(1 2 3)
scm> (cons 1 (cons (cons 2 (cons 3 nil)) nil))
(1 (2 3))

Two other common ways of creating lists is using the built-in list procedure or the quote special form:

• The list procedure takes in an arbitrary amount of arguments. Because it is a procedure, all operands are evaluated when list is called. A list is constructed with the values of these operands and is returned.
• The quote special form takes in a single operand. It returns this operand exactly as is, without evaluating it. Note that this special form can be used to return any value, not just a list.

scm> (define x 2)
scm> (define y 3)
scm> (list 1 x 3)
(1 2 3)
scm> (quote (1 x 3))
(1 x 3)
scm> '(1 x 3)   ; Equivalent to the previous quote expression
(1 x 3)
scm> '(+ x y)
(+ x y)

=, eqv?, equal?

• = can only be used for comparing numbers.
• eqv? behaves like == in Python for comparing two non-pairs (numbers, booleans, etc.). Otherwise, eqv? behaves like the Python is operator.
• equal? compares pairs by determining if their cars are equal? and their cdrs are equal? (that is, they have the same contents). Otherwise, equal? behaves like eqv?.

scm> (define a '(1 2 3))
a
scm> (= a a)
Error
scm> (equal? a '(1 2 3))
#t
scm> (eqv? a '(1 2 3))
#f
scm> (define b a)
b
scm> (eqv? a b)
#t

Questions

Q3: Warm-up

These short questions are meant to help refresh your memory of topics covered in lecture and lab this week before tackling more challenging problems.

Describe the difference between the following two Scheme expressions. (Hint: which defines a new procedure?)

Expression A:

(define x (+ 1 2 3))

Expression B:

(define (x) (+ 1 2 3))

Write an expression that selects the value 3 from the list below.

(define s '(5 4 (1 2) 3 7))

Q4: List Making

Let's make some Scheme lists. We'll make the same list with list, quote, and cons.

The following list was visualized using the draw feature of code.cs61a.org.

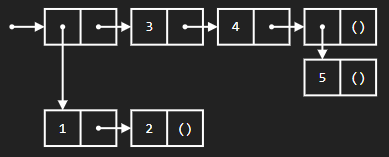
First, use list:

Run in 61A Code

Now use quote. What differences are there?

Run in 61A Code

Now try with cons. For convenience, we've defined a helpful-list and another-helpful-list:

Run in 61A Code

Q5: List Concatenation

Write a function which takes two lists and concatenates them.

Notice that simply calling (cons a b) would not work because it will create a deep list. Do not call the builtin procedure append, since it does the same thing as list-concat should do.

Run in 61A Code

scm> (list-concat '(1 2 3) '(2 3 4))
(1 2 3 2 3 4)

Q6: List Duplicator

Write a Scheme function that, when given a list, such as (1 2 3 4), duplicates every element in the list (i.e. (1 1 2 2 3 3 4 4)).

Run in 61A Code

Q7: List Insert

Write a Scheme function that, when given an element, a list, and an index, inserts the element into the list at that index. You can assume that the index is in bounds for the list.

Run in 61A Code

Exam Prep

Reminder about eval

A very useful special form in scheme is eval, which when given a scheme list, evaluates it as if it were scheme source code.

scm> (eval (list 'cons 1 (list 'cons 2 '())))
(1 2)
scm> (eval '(+ 1 2))
3
scm> (define a 'b)
a
scm> (define b 'c)
b
scm> (define c 5)
c
scm> (eval 'a)
b
scm> (eval (eval 'a))
c
scm> (eval (eval (eval 'a)))
5

You will find understanding how eval works useful for the problems below.

Q8: Directions - Fall 2014 Final Q4(c)

Difficulty: ⭐⭐

Implement the Scheme procedure directions, which takes a number n and a symbol sym that is bound to a nested list of numbers. It returns a Scheme expression that evaluates to n by repeatedly applying car and cdr to the nested list. Assume that n appears exactly once in the nested list bound to sym.

Hint: The implementation searches for the number n in the nested list s that is bound to sym. The returned expression is built during the search.

scm> (define a ’(1 (2 3) ((4))))
scm> (directions 1 ’a )
(car a)
scm> (directions 2 ’a)
(car (car (cdr a)))

Run in 61A Code

Q9: Group by Non-Decreasing

Difficulty: ⭐⭐⭐

Define a function nondecreaselist, which takes in a scheme list of numbers and outputs a list of lists, which overall has the same numbers in the same order, but grouped into lists that are non-decreasing.

For example, if the input is a stream containing elements

(1 2 3 4 1 2 3 4 1 1 1 2 1 1 0 4 3 2 1)

the output should contain elements

((1 2 3 4) (1 2 3 4) (1 1 1 2) (1 1) (0 4) (3) (2) (1))

Hint: You might want to review the nesting list structure in partition options from examprep 07

Note: The skeleton code is just a suggestion; feel free to use your own structure if you prefer.

Run in 61A Code