Discussion 3: Recursion, Tree Recursion
Recursion
A recursive function is a function that is defined in terms of itself.
Consider this recursive factorial function:
def factorial(n):
"""Return the factorial of N, a positive integer."""
if n == 1:
return 1
else:
return n * factorial(n - 1)Inside of the body of factorial, we are able to call factorial itself,
since the function body is not evaluated until the function is called.
When n is 1, we can directly return the factorial of 1, which is 1.
This is known as the base case of this recursive function,
which is the case where we can return from the function call directly,
without having to first recurse (i.e. call factorial) and then returning.
The base case is what prevents factorial from recursing infinitely.
Since we know that our base case factorial(1) will return,
we can compute factorial(2) in terms of factorial(1),
then factorial(3) in terms of factorial(2), and so on.
There are three main steps in a recursive definition:
Base case. You can think of the base case as the case of the simplest function input, or as the stopping condition for the recursion.
In our example,
factorial(1)is our base case for thefactorialfunction.Recursive call on a smaller problem. You can think of this step as calling the function on a smaller problem that our current problem depends on. We assume that a recursive call on this smaller problem will give us the expected result; we call this idea the "recursive leap of faith".
In our example,
factorial(n)depends on the smaller problem offactorial(n-1).Solve the larger problem. In step 2, we found the result of a smaller problem. We want to now use that result to figure out what the result of our current problem should be, which is what we want to return from our current function call.
In our example, we can compute
factorial(n)by multiplying the result of our smaller problemfactorial(n-1)(which represents(n-1)!) byn(the reasoning being thatn! = n * (n-1)!).
Q1: Warm Up: Recursive Multiplication
These exercises are meant to help refresh your memory of the topics covered in lecture.
Write a function that takes two numbers m and n and returns their product.
Assume m and n are positive integers. Use recursion, not mul or *.
Hint:
5 * 3 = 5 + (5 * 2) = 5 + 5 + (5 * 1).
For the base case, what is the simplest possible input for multiply?
For the recursive case, what does calling multiply(m - 1, n) do?
What does calling multiply(m, n - 1) do? Do we prefer one over the other?
Q2: Recursion Environment Diagram
Draw an environment diagram for the following code:
Note: If you can't move elements around, make sure you're logged in!
def rec(x, y):
if y > 0:
return x * rec(x, y - 1)
return 1
rec(3, 2)| Return value |
| Return value |
| Return value |
Note: This problem is meant to help you understand what really goes on when we make the "recursive leap of faith". However, when approaching or debugging recursive functions, you should avoid visualizing them in this way for large or complicated inputs, since the large number of frames can be quite unwieldy and confusing. Instead, think in terms of the three steps: base case, recursive call, and solving the full problem.
Q3: Find the Bug
Find the bug with this recursive function.
def skip_mul(n):
"""Return the product of n * (n - 2) * (n - 4) * ...
>>> skip_mul(5) # 5 * 3 * 1
15
>>> skip_mul(8) # 8 * 6 * 4 * 2
384
"""
if n == 2:
return 2
else:
return n * skip_mul(n - 2)Q4: Is Prime
Write a function is_prime that takes a single argument n and returns True
if n is a prime number and False otherwise. Assume n > 1. We implemented
this in Discussion 1 iteratively, now time to do it recursively!
Run in 61A CodeHint: You will need a helper function! Remember helper functions are nested functions that are useful if you need to keep track of more variables than the given parameters, or if you need to change the value of the input.
Q5: Recursive Hailstone
Recall the hailstone function from Homework 1.
First, pick a positive integer n as the start. If n is even, divide it by 2.
If n is odd, multiply it by 3 and add 1. Repeat this process until n is 1.
Write a recursive version of hailstone that prints out the values of the
sequence and returns the number of steps.
Run in 61A CodeHint: When taking the recursive leap of faith, consider both the return value and side effect of this function.
Q6: Merge Numbers
Write a procedure merge(n1, n2) which takes numbers with digits in decreasing
order and returns a single number with all of the digits of the two,
in decreasing order. Any number merged with 0 will be that number
(treat 0 as having no digits). Use recursion.
Run in 61A CodeHint: If you can figure out which number has the smallest digit out of both, then we know that the resulting number will have that smallest digit, followed by the merge of the two numbers with the smallest digit removed.
Tree Recursion
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.
For example, let's say we want to recursively calculate the
nth
Virahanka-Fibonacci number,
defined as:
def virfib(n):
if n == 0 or n == 1:
return n
return virfib(n - 1) + virfib(n - 2)Calling virfib(6) results in the following call structure that looks like
an upside-down tree (where f is virfib):
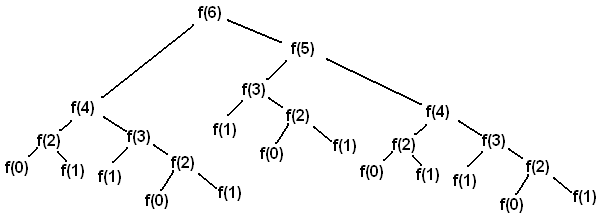
Each f(i) node represents a recursive call to virfib.
Each recursive call f(i) makes another two recursive calls,
which are to f(i-1) and f(i-2).
Whenever we reach a f(0) or f(1) node, we can directly return 0 or 1
rather than making more recursive calls, since these are our base cases.
In other words, base cases have the information needed to return an answer directly, without depending upon results from other recursive calls. Once we've reached a base case, we can then begin returning back from the recursive calls that led us to the base case in the first place.
Generally, tree recursion can be effective for problems where there are multiple possibilities or choices at a current state. In these types of problems, you make a recursive call for each choice or for a group of choices.
Q7: Count Stair Ways
Imagine that you want to go up a flight of stairs that has n steps,
where n is a positive integer.
You can either take 1 or 2 steps each time. How many different ways can you go up this flight of stairs?
In this question, you'll write a function count_stair_ways that solves this problem.
Before you code your approach, consider these questions.
How many different ways are there to go up a flight of stairs with n = 1 step? How about n = 2 steps? Try writing out some other examples and see if you notice any patterns.
What’s the base case for this question? What is the simplest input?
What do count_stair_ways(n - 1) and count_stair_ways(n - 2) represent?
Fill in the code for count_stair_ways:
Q8: Count K
Consider a special version of the count_stair_ways problem, where instead of taking 1 or 2 steps, we are able to take up to and including k steps at a time. Write a function count_k that figures out the number of paths for this scenario. Assume n and k are positive.
Run in 61A CodeHint: Your solution will follow a very similar logic to what you did for
count_stair_ways.