Discussion 7: Trees, Linked Lists

This is an online worksheet that you can work on during discussions. Your work is not graded and you do not need to submit anything.

Trees

In computer science, trees are recursive data structures that are widely used in various settings and can be implemented in many ways.

Generally in computer science, you may see trees drawn "upside-down." We say the root is the node where the tree begins to branch out at the top, and the leaves are the nodes where the tree ends at the bottom.

Some terminology regarding trees:

  • Parent Node: A node that has at least one branch.
  • Child Node: A node that has a parent. A child node can only have one parent.
  • Root: The top node of the tree.
  • Label: The value at a node.
  • Leaf: A node that has no branches.
  • Branch: A subtree of the root. Trees have branches, which are trees themselves: this is why trees are recursive data structures.
  • Depth: How far away a node is from the root. We define this as the number of edges between the root to the node. As there are no edges between the root and itself, the root has depth 0.
  • Height: The depth of the lowest (furthest from the root) leaf.

In computer science, there are many different types of trees, used for different purposes. Some vary in the number of branches each node has; others vary in the structure of the tree.

A tree has a root value and a list of branches, where each branch is itself a tree.

  • The Tree constructor takes in a value label for the root, and an optional list of branches branches. If branches isn't given, the constructor uses the empty list [] as the default.
  • To get the label of a tree t, we access the instance attributes t.label.
  • Accessing the instance attribute t.branches will give us a list of branches. Treating the return value of t.branches as a list is then part of how we define trees.

Q1: Height

Write a function that returns the height of a tree. Recall that the height of a tree is the length of the longest path from the root to a leaf.

Run in 61A Code

Q2: Maximum Path Sum

Write a function that takes in a tree and returns the maximum sum of the values along any path in the tree. Recall that a path is from the tree's root to any leaf.

Run in 61A Code

Q3: Find Path

Write a function that takes in a tree and a value x and returns a list containing the nodes along the path required to get from the root of the tree to a node containing x.

If x is not present in the tree, return None. Assume that the entries of the tree are unique.

For the following tree, find_path(t, 5) should return [2, 7, 6, 5]

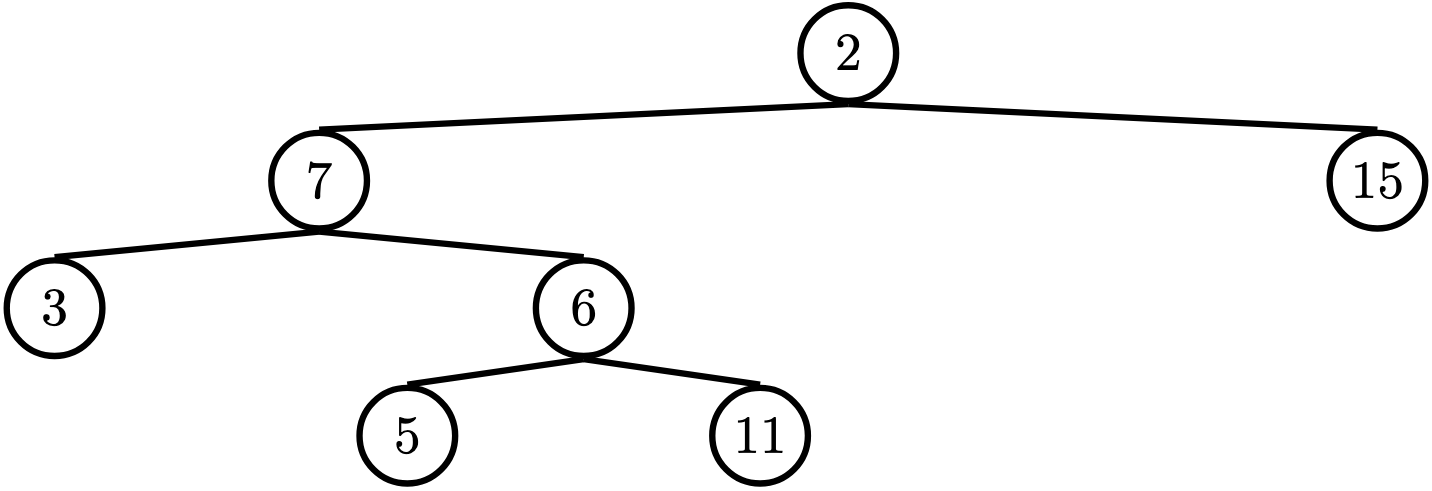
Example Tree

Run in 61A Code

Q4: Prune Small

Complete the function prune_small that takes in a Tree t and a number n and prunes t mutatively. If t or any of its branches has more than n branches, the n branches with the smallest labels should be kept and any other branches should be pruned, or removed, from the tree.

Run in 61A Code

Linked Lists

There are many different implementations of sequences in Python. Today, we'll explore the linked list implementation.

A linked list is either an empty linked list, or a Link object containing a first value and the rest of the linked list.

To check if a linked list is an empty linked list, compare it against the class attribute Link.empty:

if link is Link.empty:
    print('This linked list is empty!')
else:
    print('This linked list is not empty!')

You can find an implementation of the Link class below:

class Link:
    """A linked list."""
    empty = ()

    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest:
            rest_repr = ', ' + repr(self.rest)
        else:
            rest_repr = ''
        return 'Link(' + repr(self.first) + rest_repr + ')'

    def __str__(self):
        string = '<'
        while self.rest is not Link.empty:
            string += str(self.first) + ' '
            self = self.rest
        return string + str(self.first) + '>'

Q5: WWPD: Linked Lists

What would Python display?

Note: If you get stuck, try drawing out the box-and-pointer diagram for the linked list or running examples in 61A Code.

>>> link = Link(1, Link(2, Link(3)))
>>> link.first
>>> link.rest.first
>>> link.rest.rest.rest is Link.empty
>>> link.rest = link.rest.rest
>>> link.rest.first
>>> link = Link(1)
>>> link.rest = link
>>> link.rest.rest.rest.rest.first
>>> link = Link(2, Link(3, Link(4)))
>>> link2 = Link(1, link)
>>> link2.first
>>> link2.rest.first

Q6: Remove All

Implement a function remove_all that takes a Link, and a value, and remove any linked list node containing that value. You can assume the list already has at least one node containing value and the first element is never removed. Notice that you are not returning anything, so you should mutate the list.

Note: Can you create a recursive and iterative solution for remove_all?

Run in 61A Code

Q7: Slice

Implement a function slice_link that slices a given link. slice_link should return a new Link containing the elements of link starting at index start and ending one element before index end, just like slicing a normal Python list.

Run in 61A Code