In lecture, we mentioned red-black trees rather briefly, saying that they were representations of 2-4 trees. In this activity, we'll use them as an exercise in tree manipulation.
As a reminder, a 2-4 tree is a search tree in which each inner node has from 2 to 4 children, and from 1 to 3 keys (one fewer keys than children), except for the root, which is allowed to have one child and no keys. All leaf nodes are at the bottom of the tree and contain no data. All leaf nodes are at the same level (the same distance from the root). The search property that these trees maintain is as follows:
In a node with n keys, K1…Kn, the keys are in ascending order. The child trees, C0…Cn, have the property that all keys in the subtree rooted at Ci are less than Ki+1 for i<n and, if i>0, are greater than Ki.
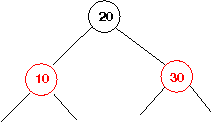
A red-black tree is an ordinary binary search tree augmented with an extra boolean value at each node, whose values are traditionally represented as the colors red or black rather than true or false. These colors maintain the following invariant, in addition to the usual binary search property:
Any 2-4 tree node can be represented by a cluster of 1–3 red-black tree consisting of one black node (possibly a leaf) with with 0–2 red children. The children of the 2-4 tree node are the black children of the root (if any) and the (necessarily black) children of the red nodes (again, if any). The precise correspondance is shown in slide #9 of Lecture #29. That slide shows five 2-4 tree nodes and their translations into clusters of red-black tree nodes. Look also at the last slide #12 (there are three), and the two-key subtree containing 30 and 27. This illustrates the one case not shown on slide #9—that a 2-4 tree node with two keys (and two children) can be represented either by two nodes where the larger key is at the root and the smaller (red) key is on the left, as on slide #12, or with the smaller key at the root and the larger (red) key on its right, as with keys 5 and 10 on slide #9.
Insertion into a red-black tree (illustrated in slide 11–12 of Lecture #29) starts out just like insertion into a binary search tree. You insert at the bottom of the tree, replacing the appropriate leaf (empty) with a red node containing the key and having two leaves as children. The rest of the process involves restoring the properties of red-black trees: equal numbers of black nodes on all paths from the root to the leaves and no red nodes with any red children. We're off to a good start in any case: adding a red node never increases the number of black nodes in a path from the root to the leaves.
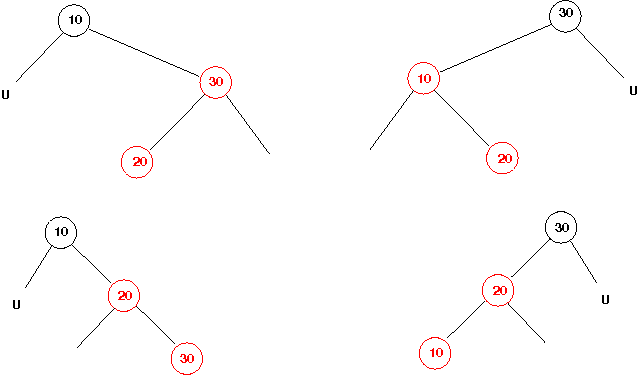
As for the rest of the problem, we repeat the following procedure until there is no red node with a red child: There will be at most one red node (call it C) with a red parent (call it P). What we do depends on the color of C's uncle (i.e., P's sibling node, call it U):