A. Introduction

This week's lab consists of these three just as a break from our usual boring lab stuff. We've used these contests to select teams for the annual ACM Collegiate Programming Contest. In the Berkeley contests, participants work alone. In the ACM competitions, they work in teams of three (with one terminal between them). Feel free to do it either way (but everyone please submit a solution, even if it is collaborative, being careful, as always to name your fellow solvers).

In the contest finals, teams try to solve collections of these problems (12 in the 2017 contest, held in Rapid City, South Dakota) in a period of 5 hours. Top contenders get very good at it (the Tokyo University team solved its problem in 2015 in 5 minutes!). No, we don't expect this of you, but take it as an indication that the problems are doable.

The skeleton files (P1.java, P2.java, and P3.java) are very skeletal indeed this time. Input to each program will come from the standard input (System.in) and output goes to the standard output.

The directories 1, 2, and 3 contain test data and expected results, which make check will use to test your solutions.

B. Getting Started

Rather than have a lab devoted to current topics in the course, we're going to have a problem-solving lab instead. You won't be graded on how much you complete successfully (as usual), but we do suggest giving it a try. The problems here come from various programming contests. The idea in these contests is to work for speed of programming. Some teams of three at the ACM International Programming Contest, for example, will solve 12 (or even 13) problems like these in five hours.

In all of these problems, the input will come from the standard input and output will go to the standard output.

You'll find (trivial) skeletons and some test data for your answers in the lab 8 directory which you can get by running.

git fetch shared
git merge shared/lab8 -m "Get lab8 skeleton"
git push

What follows are the instructions for each problem. They begin with a brief description of the problem followed by an illustrative example. At the end of each problem description you will find a table that maps example input (read from stdin) and its corresponding output (to be printed to stdout).

This will require you to write Java code that will read from System.in. A common class used to read from an input stream in competition programming is the BufferedReader class. You will want to read the buffered reader java documentation. You may also refer to this guide on how to use BufferedReader's readLine() method.

This guide shows how to read from a file. To read from System.in you may want to look at the InputStreamReader class documentation and look at how to create one for System.in. Alternatively you can use something called scanner to replace the BufferedReader and InputStreamReader combination.

C. (P1) From the Valladolid archives

An imaging device furnishes digital images of two machined surfaces that eventually will be assembled in contact with each other. The roughness of this final contact is to be estimated.

A digital image is composed of the two characters, 'X' (marking places where material is present) and 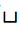(blank, indicating space).
The first column will always have an 'X' in it and will be part of the left surface. The left surface can extend to the right as contiguous Xs.

Similarly, column $N$ will always have an X in it and will be part of the right surface, where $N$ is furthest right position of any X over all rows. The right surface can extend to the left from column $N$ as contiguous Xs. Both surfaces will have the same vertical extent (the same number of rows), so that there is a section of left surface and right surface on each row of the image.

For example, here is a possible image (with blanks shown as ):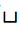

In this example, each line is 30 characters long

In each row of the image, there can be zero or more blanks separating the left surface from the right surface. There will never be more than a single blank region in any row.

For each image given, you are to determine the total empty area -- the total number of blanks between the surfaces -- that will exist after the left surface has been brought into contact with the right surface. The two surfaces are brought into contact by displacing them strictly horizontally towards each other until a rightmost X of the left surface of some row is immediately to the left of the leftmost X of the right surface of that row. There is no rotation or twisting of these two surfaces as they are brought into contact; they remain rigid, and only move horizontally.

The input consists of a series of digital images. Each image consists of one or more lines of Xs and blanks, all having the same length and all beginning and ending with X. There will be an empty line after every data set.

For each image in the series, output the total empty area, using the format shown in the example.

D. (P2) Adapted from the Valladolid archives

Consider binary trees whose nodes are labeled with single digits and letters (upper- and lowercase, case-sensitive).

Given the preorder (root, left subtree, right subtree) node order and the inorder (left subtree, root, right subtree) node order for the same tree, it is possible to reconstruct the tree, assuming no two nodes in the tree have the same label. For example, given the preorder traversal order DBACEGF and the inorder traversal order ABCDEFG you can compute that the tree these come from is

You are to write a program to do this reconstruction on any such tree.

The input consists of one or more cases in free format. Each case consists of two non-empty strings PRE and IN, representing the preorder traversal and inorder traversal of a non-empty binary tree, and consisting of letters and digits. Case is significant.

For each test case, print the reconstructed tree's postorder traversal (left subtree, right subtree, root), using the format shown in the example.

E. (P3) Due to E. W. Dijkstra

Consider decimal numerals containing only the digits 1 -- 3. A numeral is considered good if no two adjacent non-empty substrings of it are equal; otherwise it is bad. For example, the numerals 1, 12, and 1213 are good, while 11, 32121, and 121321312 are bad.

Write a program that, given $N > 0$, finds the smallest good $N$-digit numeral.
The input consists of a sequence of positive integers. For each of these integers, $N$, the output is to contain a line of the form.

The smallest good numeral of length N is S.