Navigation
- A. Set of Strings
- B. BSTStringSet Bounded Iterator
- C. ECHashStringSet Implementation
- D. ECHashStringSet Timing
- E. Amortized Runtime
- F. Submission
Introduction
This homework covers BSTs and Hashing. You'll be implementing these data structures from scratch–how cool is that! If you're looking for gentle intro, feel free to watch this introductory video. If you'd rather jump straight into the deep end though, then continue on with the spec!
A. Set of Strings
Complete the implementation of the type BSTStringSet, which implements the
interface StringSet. As the class name suggests, the intended implementation
uses a binary search tree. Don't use any of the Java Collection classes in your
BST implementation (you may still use a List implementation to collect items for
the asList method). The asList method for the BSTStringSet should return a list in sorted order. For all of the methods, we recommend using iteration, not recursion. Recursion tends to take up more space (due to the need to create new stack frames for every function call) and can end up resulting in stackoverflow errors when we do extremely large timing tests.
Hint: think about what you would like your functions to be taking in, returning, and computing. Remember that you can always make your own private helper functions.
B. BSTStringSet Bounded Iterator (Optional)
Modify BSTStringSet to implement SortedStringSet, providing an iterator that returns elements
within a specified range of values in ascending order. Even if you decide not to do this part of the assignment, you should modify your BSTStringSet to implement SortedStringSet, and uncomment the @Override in the skeleton.
The iterator should produce
its values in linear time $O(N)$, where N is the number of items in the tree.
We've provided the class BSTStringSetRangeTest to help check that your solution works in these time bounds.
The tricky part of this assignment is producing an in-order tree iterator. We've provided the class BSTIterator, which is an iterator for a full BST. You can reference this class when writing the in-order iterator.
C. ECHashStringSet
For this problem, you'll expand on your work from earlier by creating a
hashing-based implementation of the StringSet interface, which is provided in the skeleton.
To implement the interface, you'll be working almost completely
from scratch, with only minimal skeleton code that implements the interface so the code will compile.
This one will be a fair bit more difficult than the BSTStringSet. If you find yourself extremely stuck, watch the introduction video linked at the top of the spec. It will give some hints on how to get started.
Create a class ECHashStringSet (EC as in External Chaining) that implements the StringSet interface
using an external chaining hash table as its core data structure. In
order to ensure that the .put and .contains operations are fast, you should
resize the hash table as soon as the load factor exceeds 5. For memory
efficiency, we ideally would ensure that the load factor is never less than
0.2, except for empty lists, for which the load factor is allowed to
be zero.
Ask yourself why this would have an important effect on our memory usage. As a hint, imagine if we made
our set extremely long and then deleted a bunch of elements so that there is just one thing in the set:
if we didn't resize when the load factor was less than some threshold, do you see how this would be a
complete waste of space?
However, since we don't have a remove operaion, you do not need to worry about downsizing anything.
You also do not need to worry about asList returning the keys in sorted order.
There is one annoying issue you'll enounter: If the hashCode() is
negative, we need to remove the top bit (since, unlike Python, negative array indices
are not allowed in Java). You can do this using the bit operations we
discussed earlier in class, e.g. (s.hashCode() & 0x7fffffff) %
bucketCount. You should remember this from BitExercise.absolute(int x) in HW5.
There's no restriction on what you are allowed to use, but you should
avoid using any library class that has "hash"
in the name, since that would defeat the whole point of this problem.
You are allowed to use the hashCode() function for Strings.
For an extra (ungraded) challenge, don't use anything that requires using a Java library
class (except for the asList method).
As references, you might find the following resources useful:
- Chapter 7 of DSIJ.
- The Resizing Array-Based Stack, which is part of Princeton's standard Java library.
- The Wikipedia article on separate chaining (another term for external chaining).
- If you are getting "unchecked or unsafe operations" errors, you might want to look at this Stack Overflow post on creating arrays of objects that expect a formal type parameter. There is no good way to avoid the warning, aside from suppressing it. If you are curious why, check out this Stack Overflow post.
Your correctness tests from the previous part should work almost without
modification (you'll just need to change the type of object that is
instantiated). Make sure to test something that inserts a large number
of strings. One testing approach is to generate random strings, insert
them into both your ECHashStringSet and a
TreeSet<String>, then iterate through the entire
TreeSet and ensure that all of its members are also contained in your
ECHashStringSet and vice-versa.
One solution from a previous semester (which does use an import for handling the list of items that go in each bucket) is 66 lines including comments and whitespace.
If you're unsure how to get started, slide 4 from the Hashing lecture provides a visual of what our hash table will look like. Starting from this visual, try asking yourself:
- What data structure do I need to make my buckets? What about the list stored at each bucket?
- How do I know which bucket a given
Stringshould be put in? - Try implementing
putandcontains. Test that you are able to add to yourECHashStringSetand check if it contains elements. - Now, aim to satisfy the efficiency requirement with resizing. When do we want to resize the array? How do I resize an array?
D. ECHashStringSet Timing
Run the provided timing tests InsertRandomSpeedTest and InsertInOrderSpeedTest for a range of speeds. Fill out hw6timing.txt as directed. Note that hw6timing.txt has the input sizes you should be passing to InsertRandomSpeedTest and InsertInOrderSpeedTest.
If you're having timing issues, make sure your hash table is actually resizing. However, give it a minute to run. The staff solution still takes about 60 seconds to compute some of the largest tests.
E. Amortized Runtime
So now you've implemented your HashSet (or at least read the spec) and (hopefully) satisfied the runtime constraints. We have seen other data structures in this class which rarely have such good runtime. How can we store so many elements efficiently with such good runtime? How do our decisions about when and how to resize affect this?
For an intuitive metaphor for this, check out Amortized Analysis (Grigometh's Urn).
If you are more visually inclined, here is one way to visualize the runtime in the form of a graph. We'll assume here that our hashcode is very good and we don't get very many collisions (a powerful assumption). When we first create our HashSet, let's say we decide to start with an outer array of size 4. This means we can have constant runtime for our first four insertions. Each operation will only take one unit of time.
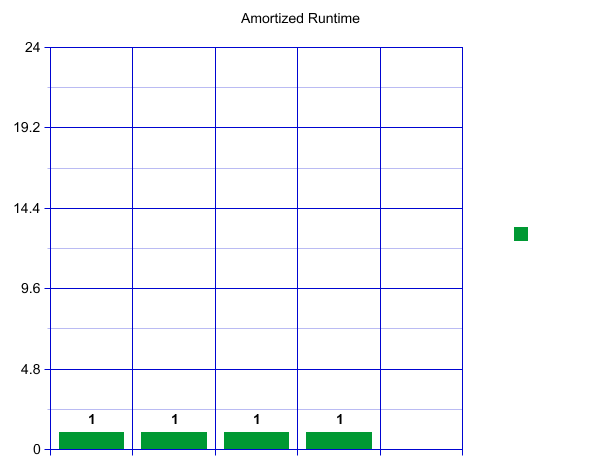
When we reach our load factor and have to resize, let's say we decide to make an array of size 8 and copy over our four current items—which takes four constant time lookups.
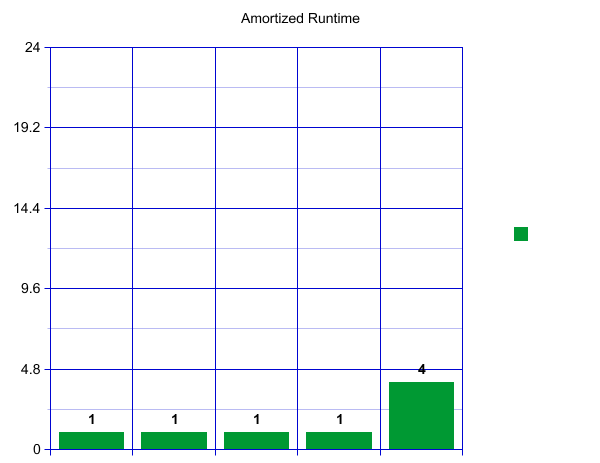
That is a big spike! How can we say this is constant? Well, we will now have eight fast inserts! Wow!

A pattern starts to emerge. Once we have again reached our load factor there will be a spike, followed by a sequence of "inexpensive" inserts. These spikes, however, are growing rapidly!
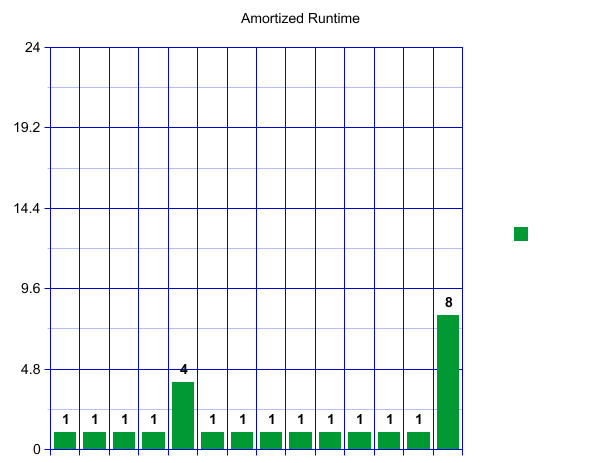
If we imagine this continuing, each spike will get bigger and bigger! Perhaps counterintuitively, this runtime, viewed over a long time, is actually constant if the work is "amortized" over all of our inserts. Here amortized means that we are spreading the cost of an expensive operation over all our operations. This gives us a constant runtime overall for a large sequence of inserts and resizes. To convince yourself of this visually, imagine "tipping" the size four spike so that it adds one operation to each of the four fast inserts before it. Now each insert operation is taking about 2 units of work, which is constant! We can see this pattern will continue. We can "tip" our size eight resize across the eight previous fast operations! Try drawing a few more resizes out and convince yourself that the spike will always fit.
We have now gotten to the heart of the efficacy of HashSets. Would we get this behavior if we picked a resizing scheme which was additive and not multiplicative?
F. Submission
Make sure you have completed your BSTStringSet, your ECHashStringSet, and your hw6timing file.
Don't forget to push both your commits and tags for your final submission. As a reminder, you can push your tags by running:
$ git push --tags