Navigation
- A. Intro
- B. The Priority Queue Abstract Data Type
- C. Review: Heaps
- D. Exercise: Implementing Your Own Min Heap
- E. Application: Heapsort
- F. Heapify
- G. Submission
A. Intro
Here's an optional intro video for the lab with some explanations and examples. All the information in the video is covered in the spec and timestamps for topics are in the video description.
Today, we'll take a look at the priority queue and how it can be implemented
using a heap. We'll then implement our own priority queue (called ArrayHeap),
and then discuss some applications of heaps.
As always, you can get the skeleton of this lab with the following commands.
git fetch shared
git merge shared/lab9 -m "get lab9 skeleton"
git pushB. The Priority Queue Abstract Data Type
We’ve learned about a few abstract data types already, including the stack and queue. The stack is a last-in-first-out (LIFO) abstract data type where, much like a physical stack, we remove most recently added elements first. The queue is a first-in-first-out (FIFO) abstract data type. When we remove items from a queue, we remove the least recently added elements first.
For example, you can model the back button in your browser as a stack - if you hit it, the most recent page you visited is the one you go to. You can model the GBC burrito bowl line as a queue - the first people to get in line get served first. But what if we want to model an emergency room, where people waiting with the most urgent conditions are served first? We would need to serve patients based on how urgent their condition is, and not by how long ago they arrived.
Sometimes, processing items LIFO or FIFO is not what we want. We may instead want to process items in order of importance or a priority value.
The priority queue is an abstract data type that allows for this that contains the following methods:
insert(item, priority value): Insertsiteminto the priority queue withpriority valuepriority.poll(): Removes and returns the highest priority item in the priority queue.peek(): Returns the highest priority item.
Note: The priority of items are a function of their priority values. In a max priority queue, elements with larger priority values will have higher priority. In a min priority queue, elements with smaller priority values will have higher priority. In this lab, you will be dealing with the latter: Items with smaller priority values have higher priorities and should be removed from the priority queue first.
Java’s PriorityQueue class is implemented with a data structure
called a binary min heap. For the remainder of this lab, we will study the heap
data structure and create our own implementation of a priority queue using a
binary min heap.
C. Review: Heaps
Heaps were covered in lecture 23. This section is just a reference. Feel free to skip this section if you are already familiar with heaps and come back to this later if you get stuck.
Heap Properties
Heaps are tree-like structures that follow two additional invariants that will be discussed more below. Normally, elements in a heap can have any number of children, but in this class we will restrict our view to binary heaps, where each element will have at most two children.
Invariant 1: Completeness
In order to keep our operations fast, we need to make sure the heap is well balanced. We will define balance in a binary heap's underlying tree-like structure as completeness.
A complete tree has all available positions for elements filled, except for possibly the last row, which must be filled left-to-right. A heap's underlying tree structure must be complete.
Here are some examples of trees that are complete:
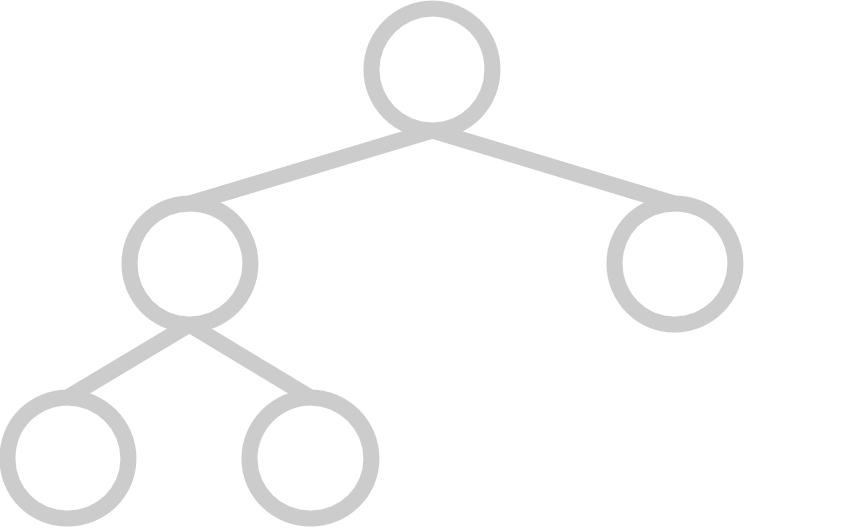
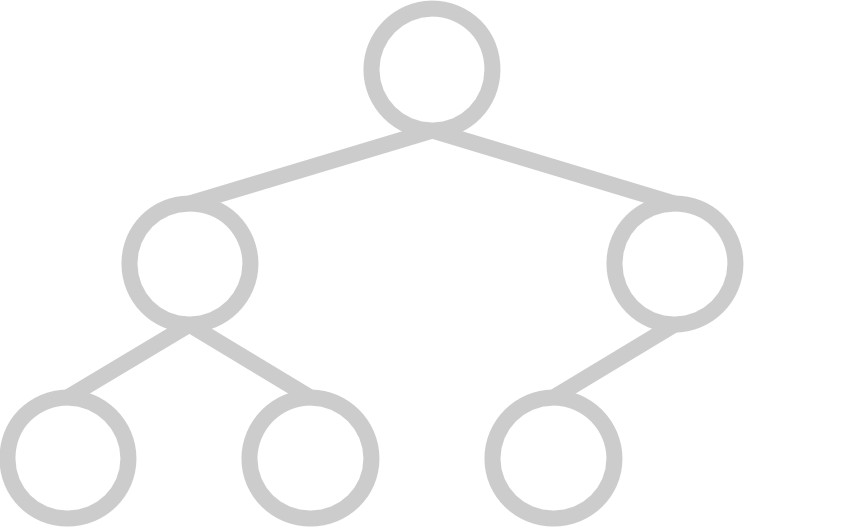
And here are some examples of trees that are not complete:
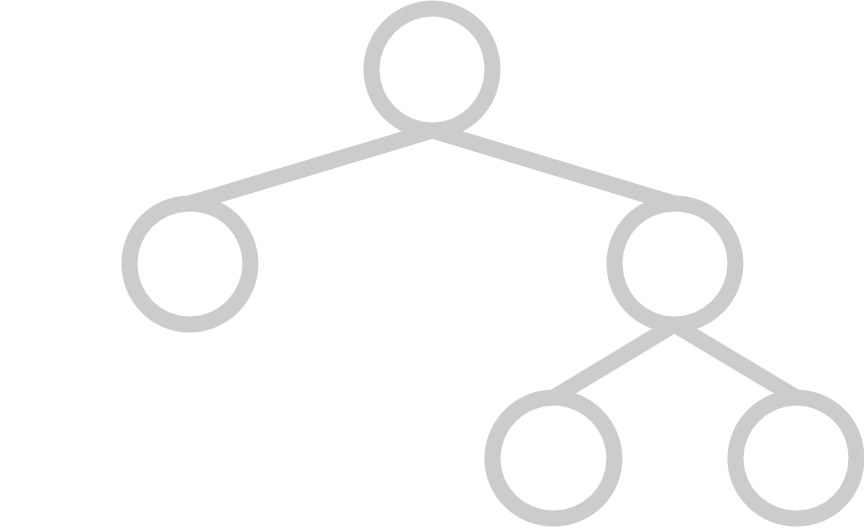
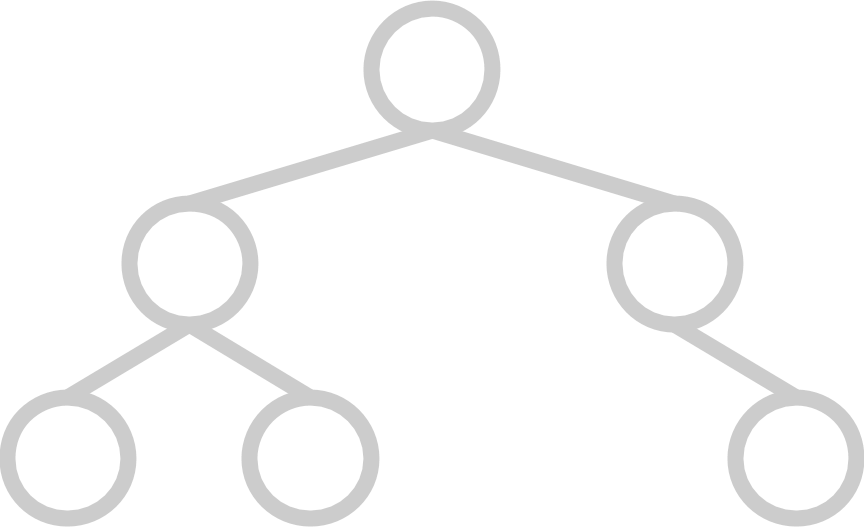
Invariant 2: Heap Property
Here is another property that will allow us to organize the heap in a way that will result in fast operations.
Every element must follow the heap property, which states that each element must be smaller than all of its children or larger than those of all of its children. The former is known as the min-heap property, while the latter is known as the max-heap property.
If we have a min heap, this guarantees that the element with the lowest priority value will always be at the root of the tree. This helps us access that item quickly, which is what we need for a priority queue!
For the rest of this lab, we will be discussing the representation and operations of binary min heaps. However, this logic can be modified to apply to max heaps or heaps with any number of children.
Heap Representation
We can represent binary trees as arrays. (In this lab, we use ArrayLists.)
- The root of the tree will be in position 1 of the array (nothing is at position 0; this is to to make indexing more convenient).
- The left child of a node at position $i$ is at position $2i$.
- The right child of a node at position $i$ is at position $2i + 1$.
- The parent of a node at position $i$ is at position $i / 2$ rounding down.
Here is an example of a binary tree that contains a letter at each node and its array representation below. As we can see, the node B is at index 2 and its left child D is at index 2 * 2 = 4 and its right child E is at index 2 * 2 + 1 = 5. Node G is at index 7 and its parent C is at index 7 / 2 = 3 (rounding down).
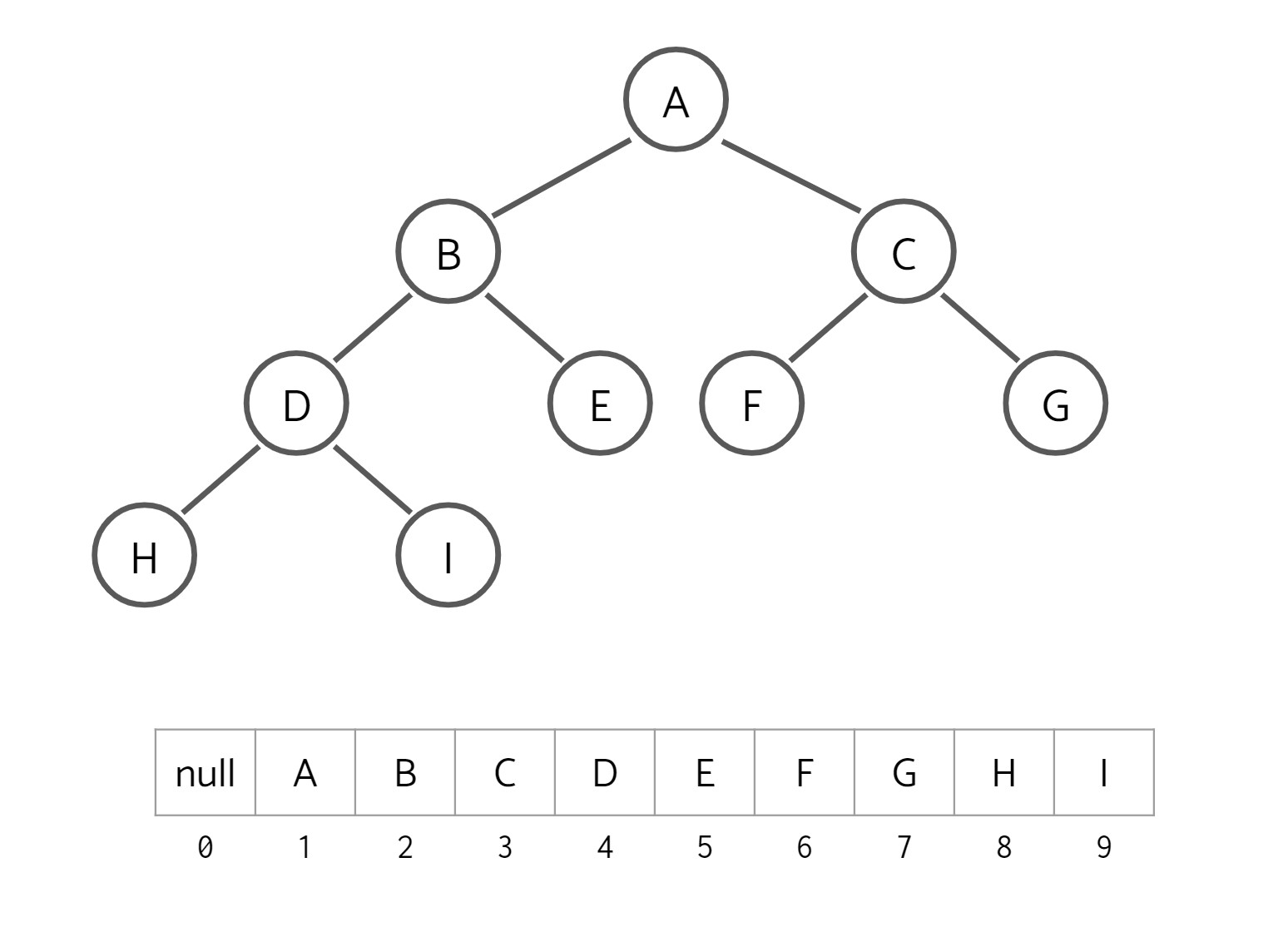
Because binary heaps are essentially binary trees, we can use this array representation to represent our binary heaps!
Heap Operations
For min heaps, there are four operations that we care about:
insert
: Inserting an element to the heap.
removeMin
: Removing and returning the item with the lowest priority value.
peek
: Returning the lowest priority value item without removal.
changePriority
: Changes the priority of an item to a new priority value.
When we do these operations, we need to make sure to maintain the invariants mentioned earlier (completeness and the heap property). Let's walk through how to do each one.
insert
- Put the item you're adding in the next available spot in the bottom row of the tree. This is equivalent to placing the element in the next free spot in the array representation of the heap. This ensures the completeness of the heap because we're filling in the bottom-most row left to right.
If the element that has just been inserted is
n, swapnwith its parent as long asn's priority value is smaller than its parent or untilnis the new root. Ifnis equal to its parent, you can either swap the items or not.This process is called bubbling up (or swimming), and this ensures the min-heap property is satisfied because once we finish bubbling
bup, all elements belowbmust be greater than it, and all elements above must be less than it.
removeMin
- Swap the element at the root with the element in the bottom rightmost position of the tree. Then, remove the right bottommost element of the tree (which should be the previous root and the minimum element of the heap). This ensures the completeness of the tree.
If the new root
nis greater than either of its children, swap it with that child. If it is greater than both of its children, choose the smaller of the two children. Continue swappingnwith its children in the same manner untilnis smaller than its children or it has no children. Ifnis equal to both of its children or is equal to the lesser of the two children, you can choose to swap the items or not.This is called bubbling down (or sinking), and this ensures the min-heap property is satisfied because we stop bubbling down only when the element
Nis less than both of its children and also greater than its parent.
findMin / peek
The element with the smallest value will always be stored at the root due to the min-heap property. Thus, we can just return the root node, without changing the structure of the heap.
changePriority
Find the element whose priority you want to change and change its priority value. Then bubble up or bubble down the element accordingly.
D. Exercise: Implementing Your Own Min Heap
The class ArrayHeap implements a binary min heap using an underlying ArrayList.
Open it up and read the provided methods.
Notice in the constructor we call contents.add(null). Think about how this
affects indexing and why we choose to add a null element.
Fill in the incomplete methods in ArrayHeap.java (marked with TODOs) You should not edit the methods without TODOs but you can use them in the code you write. As John DeNero wisely says,
code that doesn't respect abstraction barriers should BURN. Respect abstraction
barriers! (You should able to finish the lab without directly accessing the
contents ArrayList.)
- First implement
getLeftOf(int i),getRightOf(int i),getParentOf(int i). - Next, implement
min(int index1, int index2),peek(),bubbleUp(int index),bubbleDown(int index) - Implement
insert(T item, double priority),removeMin(). Make sure you use thebubbleUpandbubbleDownhelper methods when implementing these functions. After implementing, you should now be passing the testsinsertOne,insertAscending,insertDescending,insertMany, andremoveMinPeekNull. - Implement
changePriority(T item, double priority). Make sure you use thebubbleUpandbubbleDownhelper methods when implementing this functions. After implementing, you should now be passing the testschangePriorityIncreaseOne,changePriorityDecreaseOne, andchangePriorityAll.
All tests are located in ArrayHeapTest.java.
E. Application: Heapsort
Now, let’s move onto an application of the heap data structure. Suppose you have an array of $N$ numbers that you want to sort smallest-to-largest. One algorithm for doing this is as follows:
- Put all of the numbers in a min heap.
- Repeatedly remove the min element from the heap, and store them in an array in that order.
This is called heapsort.
Now, what is the runtime of this sort? Since each insertion takes proportional to $\log N$ comparisons once the heap gets large enough and each removal also takes proportional to $\log N$ comparisons, the whole process takes proportional to $N \log N$ comparisons.
It turns out we can actually make step 1 of heapsort run faster—proportional to $N$ comparisons—using a process called heapify. (Unfortunately, we can’t make step 2 run any faster than $N \log N$, so the overall heapsort must take $N \log N$ time.)
F. Heapify
The algorithm for taking an arbitrary array and making it into a min (or max) heap in time proportional to $N$ is called heapify. Pseudocode for this algorithm is below:
def heapify(array):
index = N / 2
while index > 0:
bubble down item at index
index -= 1Conceptually, you can think of this as building a heap from the bottom up. To get a visualization of this algorithm working, click on the BuildHeap button on USFCA interactive animation of a min heap. This loads a pre-set array and then runs heapify on it.
Try to describe the approach in your own words. Why does the index start at the middle of the array rather than the beginning, 0, or the end, N? How does each bubble down operation maintain heap invariants?
It is probably not immediately clear to you why this heapify runs in $O(N)$. For those who are curious, you can check out an explanation on StackOverflow or Wikipedia.
G. Submission
Please submit ArrayHeap.java and your partner.txt file (left blank if you did not work with a partner). The grader for this assignment will be the same as the tests that we have provided for you. You must pass 5/8 tests for full credit for this lab, but we recommend you try to pass all 8 tests.