Updates
- 09/17 : Project 1 release.
- 09/18 : Fixed typo in example output (quilt2)
- 09/24 : Project 1-2 release.
- 09/25 : Fixed some typos.
- 09/27 : Fixed some typos.
Clarifications/Reminders
- Start Early!
- This project should be done on either the hive machines. Parts of your program may not work on other computers.
- It is suggested that you work with one partner for this project. You may share code with your partner, but ONLY your partner. The submit command will ask you for your partner's name, so only one partner needs to submit. (It would be nice if only one partner submitted).
- Make sure you read through the project spec before starting.
Goals
This project will expose you to C and MIPS in greater depth. The first part gives you the opportunity to sharpen your C programming skills that you have learned in the past few weeks, while the second part dives deeper into coding MIPS. Part of this project will also serve as the basis for the upcoming project 3. We hope you will have fun!
Background
Cameras traditionally capture a two dimensional projection of a scene. However depth information is important for many real-world application. For example, robotic navigation, face recognition, gesture or pose recognition, 3D scanning and more. The human visual system can preceive depth by comparing the images captured by our two eyes. This is called stereo vision. In this project we will experiment with a simple computer vision/image processing technique, called "shape from stereo" that, much like humans do, computes the depth information from stereo images (images taken from two locations that are displaced by a certain amount).
Depth Perception
Humans can tell how far away an object is by comparing the position of the object is in left eye's image with respect to right eye's image. If an object is really close to you, your left eye will see the object further to the right, whereas your right eye will see the object to the left. A similar effect will occur with cameras that are offset with respect to each other as seen below.
The above illustration shows 3 objects at different depth and position. It also shows the position in which the objects are projected into image in camera 1 and camera 2. As you can see, the closest object (green) is displaced the most (6 pixels) from image 1 to image 2. The furthest object (red) is displaced the least (3 pixels). We can therefore assign a displacement value for each pixel in image 1. The array of displacements is called displacement map. The figure shows the displacement map corresponding to image 1.
Your task will be to find the displacement map using a simple block matching algorithm. Since images are two dimensional we need to explain how images are represented before going to describe the algorithm.
Below is a classic example of left-right stereo images and the displacement map shown as an image.

Part 1 (Due 9/24 @ 23:59:59)
Objective
In this project, we will attempting to simulate depth perception on the computer, by writing a program that can distinguish far away and close by objects.
Getting started
Copy the files in the directory ~cs61c/proj/01 to your proj1 directory, by entering the following command:
$ mkdir ~/proj1 $ cp -r ~cs61c/proj/01/* ~/proj1
The files you will need to modify and submit are:
-
calc_depth.c: Creates a depth map out of two images. You will be implementing thecalc_depth()function. -
make_qtree.c: Creates a quadtree representation from a depth map. You will be implementing thedepth_to_quad()andhomogenous()functions. -
proj1_1A.txt: Your answers to the followup questions will be in here.
You are free to define and implement additional helper functions, but if you want them to be run when we grade your project, you must include them in calc_depth.c or make_qtree.c. Changes you make to any other files will be overwritten when we grade your project.
The rest of the files are part of the framework. It may be helpful to look at all the other files.
Makefile: Defines all the compilation commands.depth_map.c: Loads bitmap images and calls the calc_depth() to calculate the depth map.calc_depth.h: Defines the signature for the calc_depth() function you will implement.make_qtree.h: Defines the signature for the depth_to_quad() and homogenous() functions you will implement.quadtree.h: Defines the qNode struct, as well as quadtree.c function headers.quadtree.c: Calls depth_to_quad() and free_qtree().utils.h: Defines Image struct and utility function signatures.utils.c: Defines bitmap loading, printing, and saving functions.test/: Contains the files necessary for testing. images/ holds input images, output will contain output files created by the program, and expected/ has the correct output of the tests.
Task A (Due 9/24)
Your first task will be to implement the depth map generator. This function takes two input images (unsigned char *left and unsigned char *right), which represent what you see with your left and right eye, and generates a depth map using the output buffer we allocate for you (unsigned char *depth_map).
Generating a depth map
In order to achieve depth perception, we will be creating a depth map. The depth map will be a new image (same size as left and right) where each "pixel" is a value from 0 to 255 inclusive, representing how far away the object at that pixel is. In this case, 0 means infinity, while 255 means as close as can be. Consider the following illustration:

The first step is to take a small patch (here 5x5) around the green pixel. This patch is represented by the red rectangle. We call this patch a feature. To find the displacement, we would like to find the corresponding feature position in the other image. We can do that by comparing similarly sized features in the other image and choosing the one that is the most similar. Of course, comparing against all possible patches would be very time consuming. We are going to assume that there's a limit to how much a feature can be displaced -- this defines a search space which is represented by the large green rectangle (here 11x11). Notice that, even though our images are named left and right, our search space extends in both the left/right and the up/down directions. Since we search over a region, if the "left image" is actually the right and the "right image" is actually the left, proper distance maps should still be generated.
The feature (a corner of a white box) was found at the position indicated by the blue square in the right image.
We'll say that two features are similar if they have a small Squared Euclidean Distance. If we're comparing two features, A and B, that have a width of W and height of H, their Squared Euclidean Distance is given by:
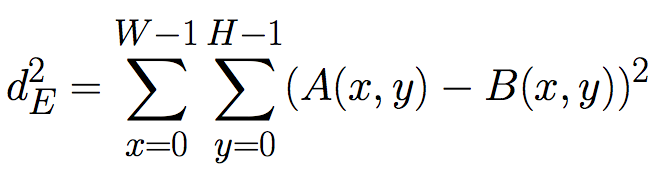
(Note that this is always a positive number.)
For example, given two sets of two 2×2 images below:
 ← Squared Euclidean distance is (1-1)2+(5-5)2+(4-4)2+(6-6)2 = 0 →
← Squared Euclidean distance is (1-1)2+(5-5)2+(4-4)2+(6-6)2 = 0 →
 ← Squared Euclidean distance is (1-3)2+(5-5)2+(4-4)2+(6-6)2 = 4 →
← Squared Euclidean distance is (1-3)2+(5-5)2+(4-4)2+(6-6)2 = 4 →
(Source: http://cybertron.cg.tu-berlin.de/pdci08/imageflight/descriptors.html)
Once we find the feature in the right image that's most similar, we check how far away from the original feature it is, and that tells us how close by or far away the object is.
Definitions (Inputs)
We define these variables to your function:
- image_width
- image_height
- feature_width
- feature_height
- maximum_displacement
We define the variables feature_width and feature_height which result in
feature patches of size: (2 × feature_width + 1) × (2 × feature_height + 1). In the
previous example, feature_width = feature_height = 2 which gives a 5×5 patch. We also define the variable
maximum_displacement which limits the search space. In the previous example maximum_displacement = 3 which
results in searching over (2 × maximum_displacement + 1)2 patches in the second image to compare with.
Definitions (Output)
In order for our results to fit within the range of a unsigned char, we output the normalized displacement between the left feature and the corresponding right feature, rather than the absolute displacement. The normalized displacement is given by:
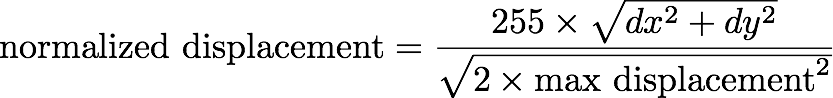
This function is implemented for you in calc_depth.c.
In the case of the above example, dy=1 and dx=2 are the vertical and horizontal displacement of the green pixel. This formula will guarantee that we have a value that fits in a unsigned char, so the normalized displacement is 255 × sqrt(1 + 22)/sqrt(2 × 32) = 134, truncated to an integer.
Bitmap Images
We will be working with 8-bit grayscale bitmap images. In this file format, each pixel takes on a value between 0 and 255 inclusive,
where 0 = black, 255 = white, and values in between to various shades of gray. Together, the pixels
form a 2D matrix with image_height rows and image_width columns.
Since each pixel may be one of 256 values, we can represent an image in memory using an array of unsigned char of size
image_width * image_height. We store the 2D image in a 1D array such that each row of the image occupies a contiguous
part of the array. The pixels are stored from top-to-bottom and left-to-right (see illustration below):
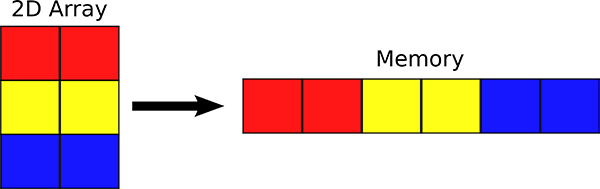
(Source: http://cnx.org/content/m32159/1.4/rowMajor.png)
We can refer to individual pixels of the array by specifying the row and column it's located in. Recall that in a matrix,
rows and columns are numbered from the top left. We will follow this numbering scheme as well, so the leftmost red square
is at row 0, column 0, and the rightmost blue square is at row 2, column 1. In this project, we will also refer to an element's
column # as its x position, and it's row # as its y position. We can also call the # of columns of the image
as its image_width, and the # of rows of the image as its image_height. Thus, the image above has a width of 2, height of 3,
and the element at x=1 and y=2 is the rightmost blue square.
Your task
Edit the function in calc_depth.c so that it generates a depth map and stores it in unsigned char *depth_map, which points to a pre-allocated buffer of size image_width × image_height. Two images, left and right are provided. They are also of size image_width × image_height. The feature_width and feature_height parameters are described in the Generating a depth map section.
Here are some implementation details and tips:
- A feature is a box of width
2 × feature_width + 1and height2 × feature_height + 1, with the original position of the pixel at its center. - You may not assume
feature_height=feature_width=maximum_displacement. They may all be different (e.g. your feature box may be a rectangle). - Pixels on the edge of the image, whose left-image features don't fit inside the image, should have a distance of 0 (infinity).
- When
maximum_displacementis 0, the whole image would have a normalized displacement of 0. - Your algorithm should not consider right-image features that lie partially outside the image area. However, if the left-image feature of a pixel is fully within the image area, you should always be able to assign a normalized displacement to that pixel.
- The source pixels always come from
unsigned char *left, whereas theunsigned char *rightimage is always the one that is scanned for nearby features. - You may not assume that
unsigned char *depth_maphas been filled with zeros. - You may not store global variables that persist between multiple calls to
calc_depth. - The Squared Euclidean Distance should be calculated according to the formula:
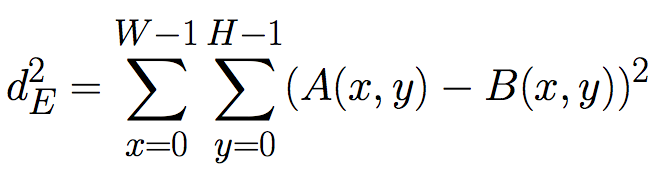
- After finding the matching feature in the right image with the smallest Squared Euclidean Distance, the normalized displacement of the pixel is given by the formula:
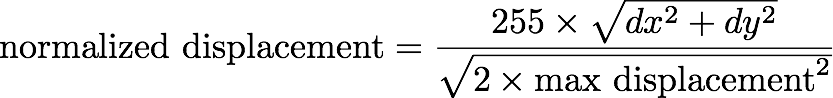
- Ties in the Euclidean Distance should be won by the one with the smallest resulting normalized displacement.
- Some test cases are provided by
make check. These are not all of the tests that we will be grading your project on.
Usage
Use make to compile the calc_depth. Your code must compile with the given Makefile:
$ make
gcc -Wall -g -std=c99 -o ....
....
You can now run ./depth_map to see the options that the program takes.
$ ./depth_map
USAGE: ./depth_map [options]
REQUIRED
-l [LEFT_IMAGE] The left image
-r [RIGHT_IMAGE] The right image
-w [WIDTH_PIXELS] The width of the smallest feature
-h [HEIGHT_PIXELS] The height of the smallest feature
-t [MAX_DISPLACE] The threshold for maximum displacement
OPTIONAL
-o [OUTPUT_IMAGE] Draw output to this file
-v Print the output to stdout as readable bytes
The -o option will let you visualize your depth map as a BMP image that you can open in your file browser. In these images, blue regions are far away and red regions are close by.
A testing framework and a few sample tests are provided for you. These tests are not a guarantee of the correctness of your code. Your code will be graded on its correctness, not whether or not it passes these tests. You can run the testing framework with make check. For calc_depth, the output images and bytes will be written to test/output/TEST_NAME-output.bmp and test/output/TEST_NAME-output.txt. For quadtree, the printed output is written to test/output/TEST_NAME-output.txt.
You can use your own 8-bit grayscale BMP images to test your code. There are helper functions in utils.c to generate BMP files from unsigned char arrays. Alternatively, you can generate them with an image editing program like Photoshop.
$ ./depth_map -l test/images/quilt2-left.bmp -r test/images/quilt2-right.bmp -h 0 -w 0 -t 1 -o test/output/quilt2-output.bmp -v
00 00 00
00 ff 00
00 00 b4
Followup questions
After implementing your depth map generator, please answer the following questions in proj1_1A.txt:
-
The images
real1-left.bmpandreal1-right.bmpin thetest/images/folder are actual photographs of a sticky note on a window (close by) against a distant background (far away). Run./depth_mapwithfeature_width=feature_height= 3 andmaximum_displacement= 14. Save the depth map BMP to a file namedtest/output/real1-output.bmp(see the Usage section about how to do this). (Protip: Themake checkcommand will also generate the imagetest/output/real1-output.bmpfor you.) How well does the algorithm identify the sticky note? Does it mistakenly identify other things as "close by" as well? (It should.) Explain why. -
Repeat #1 with
real2-left.bmpandreal2-right.bmp. Does the algorithm work better or worse on these images? Why or why not? -
Run
./depth_mapwithtest/images/cal1-left.bmpandtest/images/cal1-right.bmp. Usefeature_width=feature_height= 0, andmaximum_displacement = 3. Save the BMP output totest/output/cal1-output-0.bmp. Now, try setting the values offeature_widthandfeature_heightto 1. Then try 2. Then try 3. Save the BMP outputs totest/output/cal1-output-1.bmp,test/output/cal1-output-2.bmp, andtest/output/cal1-output-3.bmp. How do the output images change as you increase the size of the features? Explain why this happens.
Task B (Due 9/24)
Your second task will be to implement quadtree compression. This function takes a depth map (unsigned char *depth), and generates a recursive data structure called a quad tree.
Quadtree Compression
The depth maps that we create in this project are just 2D arrays of unsigned char. When we interpret each value as a square pixel, we can output a rectangular image. We used bitmaps in this project, but it would be incredibly space inefficient if every image on the internet were stored this way, since bitmaps store the value of every pixel separately. Instead, there are many ways to compress images (ways to store the same image information with a smaller filesize). In task B, you will be asked to implement one type of compression using a data structure called a quadtree.
A quadtree is similar to a binary tree, except each node must have either 0 children or 4 children. When applied to a square bitmap image whose width and height can be expressed as 2N, the root node of the tree represents the entire image. Each node of the tree represents a square sub-region within the image. We say that a square region is homogenous if its pixels all have the same value. If a square region is not homogenous, then we divide the region into four quadrants, each of which is represented by a child of the quadtree parent node. If the square region is homogeneous, then the quadtree node has no children and instead, has a value equal to the color of the pixels in that region.
We continue checking for homogeneity of the image sections represented by each node until all quadtree nodes contain only pixels of a single grayscale value. Each leaf node in the quadtree is associated with a square section of the image and a particular grayscale value. Any non-leaf node will have a value of 256 (outside the grayscale range) associated with it, and should have 4 child nodes.
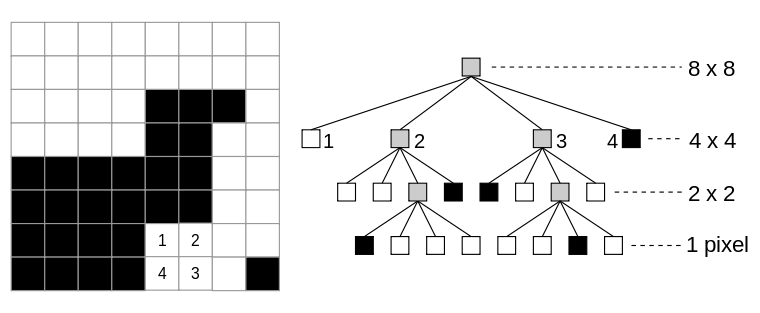
(Source: http://en.wikipedia.org/wiki/File:Quad_tree_bitmap.svg)
We will be numbering each child node created (1-4) clockwise from the top left square, as well with their ordinal direction (NW, NE, SE, SW). When parsing through nodes, we will use this order: 1: NW, 2: NE, 3: SE, 4: SW.
Given a quadtree, we can choose to only keep the leaf nodes and use this to represent the original image. Because the leaf nodes should contain every color value represented, the non-leaf nodes are not needed to reconstruct the image. This compression technique works well if an image has large regions with the same grayscale value (artificial images), versus images with lots of random noise (real images). Depth maps are a relatively good input, since we get large regions with similar depths.
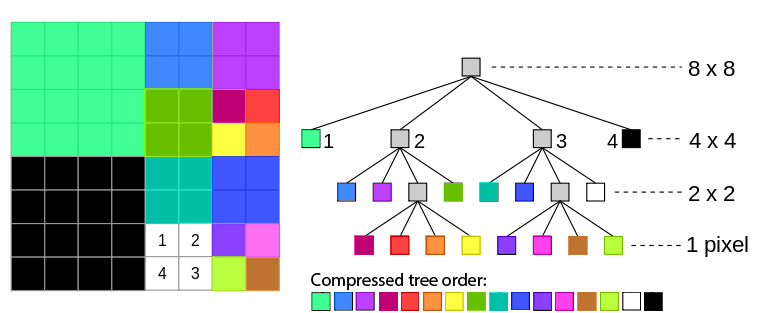
Your Job
Your task is to write the depth_to_quad() and homogenous() functions located in make_qtree.c.
The first function, depth_to_quad() takes an array of unsigned char, converts it into a quadtree, and returns a
pointer to the root qNode in the tree. Keep in mind that local variables don't last after your function returns, so you must use
dynamic memory allocation in the function. Since memory allocation could fail, you need to check whether the pointer
returned by malloc() is valid or not. If it is NULL, you should call allocation_failed() (defined in utils.h).
Your representation should use a tree of qNodes, all of which either have 0 or 4 children. The declaration of the struct qNode is in quadtree.h.
The second function homogenous() takes in the depth_map as well as a region of the image (top left coordinates, width, and height). If every pixel in that region has the same grayscale value, then homogenous() should return that value. Or else, if the section is non-homogenous, it should return 256.
Here are a few key points regarding your quadtree representation:
- Leaves should have the boolean value leaf set to 1, while all other nodes should have it as 0.
- The gray_value of leaves should be set to their grayscale value, but non-leaves should take on the value 256.
- The x and y variables should hold the top-left pixel coordinate of the image section the node represents.
- We only require that your code works with images that have widths that are powers of two. This means that all qNode sizes will also be powers of two and the smallest qNode size will be one pixel.
- The four child nodes are marked with ordinal directions (NW, NE, SE, SW), which you should match closely to the corresponding sections of the image.
- Some test cases are provided by
make check. These are not all of the tests that we will be grading your project on. - Don't worry about NULL images or images of size zero, we won't test for these (but you're welcome to have a check for it anyways and return null)
The following example illustrates these points:
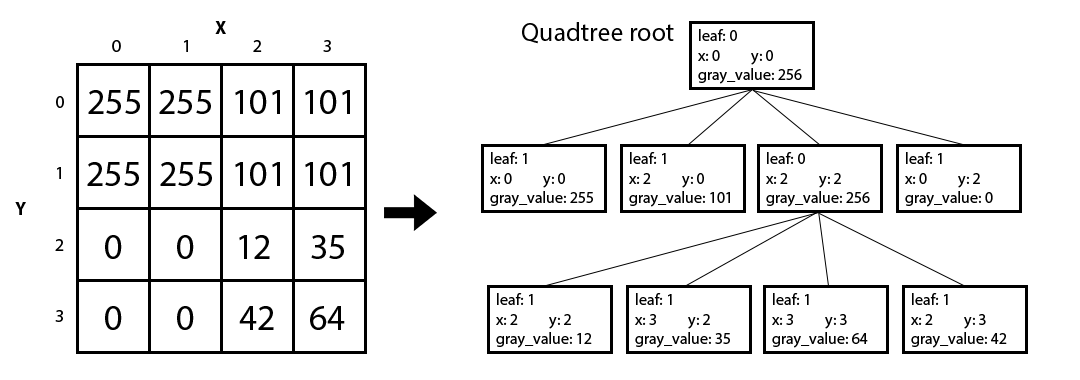
You can compile your code for task B with the following command:
$ make quadtree
Running the program with no arguments will print out the quadtree and compressed representation for a few arrays defined in print_basic(). You can also pass in the name of a grayscale bitmap image, and the code will compress the image and print out the quadtree and compressed representations (although we have not included any tests). Note that for any images whose dimensions are not square powers of two, the program will grab a square section at the approximate center of the image.
Debugging and Testing
Your code is compiled with the -g flag, so you can use GDB to help debug your program. While adding in print statements can be helpful, GDB can make debugging a lot quicker, especially for memory access-related issues. While you are working on the project, we encourage you to keep your code under version control. However, if you are using a hosted repository, please make sure that it is private, or else it could be viewed as a violation of academic integrity.
In addition, we have included a few functions to help make development and debugging easier:
- print_image(const unsigned char *data, int width, int height): This function takes in an array of pixels and prints their values in hex to standard output.
- save_image(char *filename, const unsigned char *data, int width, int height): This function takes in an array of pixels and saves them to a new bmp file at a specified filename.
- print_qtree(qNode *qtree_root): This function takes in a qNode and prints out the quadtree.
- print_compressed(qNode *qtree_root): This function takes in a qNode and prints out the compressed representation of the quadtree.
The test cases we provide you are not all the test cases we will test your code with. You are highly encouraged to write your own tests before you submit. Feel free to add additional tests into the skeleton code, but do not make any modifications to function signatures or struct declarations. This can lead to your code failing to compile during grading.
Running make check will run the test cases against your code. You will see results like this:
$ make check
Running: ./depth_map -l test/images/quilt1-left.bmp -r test/images/quilt1-right.bmp -h 0 -w 0 -t 1 -o test/output/quilt1-output.bmp -v
Wrong output. Check test/output/quilt1-output.txt and test/expected/quilt1-expected.txt
...
You can open up test/output/quilt1-output.bmp with an image viewer to see what kind of depth map your algorithm produced. You can open up test/output/quilt1-output.txt with a text editor to see the actual values it produced. The expected values will be in test/expected/quilt1-expected.txt.
If you mistakenly break parts of the skeleton, you can always grab a new copy of the file by running the following command, but BE VERY CAREFUL not to overwrite all your work.
$ cp ~cs61c/proj/01/<NAME OF FILE> ~/proj1
Before you submit, make sure you test your code on the Hive machines. We will be grading your code there. IF YOUR PROGRAM FAILS TO COMPILE, YOU WILL AUTOMATICALLY GET A ZERO FOR THAT PORTION (ie. If depth_map works but quadtree doesn't compile, you will receive points for depth_map but none for quadtree). There is no excuse not to test your code.
Submission
The full proj1-1 is due Wednesday To submit the full proj1-1, enter in the following. You should be turning in calc_depth.c, make_qtree.c, and proj1_1A.txt.
$ cd ~/proj1 $ submit proj1-1
Part 2 (Due 10/1 @ 23:59:59)
Objective
In the first part of the project we looked at a simple computer vision algorithm that generates displacement maps from stereo images. We also looked at compressing the displacement maps using a quadtree data structure. In this part you will implement a complementary task. We will use displacement maps to generate so called, random dot autostereograms. Random dot autostereograms are random-like images that when viewed wall-eyed or cross-eyed will give your brain the illusion of a 3D image. If you think about it, the entire project will enable you to capture 3D data from the environment and then visualize it in a 3D autostereogram!!!
As a complement to the quadtree compression, you will implement a decompression procedure that returns a displacement map from a quad-tree data structure.
Random-dot-autostereograms are also known by the name Magic Eye. They are very cool, but some people may have difficulty seeing the 3D scene. In fact, there's a certain percentage of the population that is incapable of seeing the 3D scene at all. With almost 800 in the class almost surely some people will not be able to view them. We appologize for that! However, you will still be able to generate your own and show it to your friends and family. For some background, more info and methods to view the autostereograms, we recommend that you look at this Wikipedia article. In particular, look at the viewing techniques section. The first autostereogram below will show an embossment of "Cal" when viewed wall-eyed. When viewed cross-eyed, it will flip and show it as a carving or a mold. The second autostereogram is reversed and will show an embossment when viewed cross-eyed and a mold when viewed wall-eyed.


Getting started
Copy the files in the directory ~cs61c/proj/01-2 to your proj1-2 directory, by entering the following command:
$ mkdir ~/proj1-2 $ cp -r ~cs61c/proj/01-2/* ~/proj1-2
The files you will need to modify and submit are:
-
calc_autostereogram.s: Creates an autostereogram. You will implement thecalc_autostereogram()function. -
lfsr_random.s: Generates a random number using a LFSR. You will implement thelfsr_random()function. -
quad2matrix.s: Coverts a quadtree into the original image. You will implement thequad2matrix()function.
You are free to define and implement additional helper functions, but if you want them to be run when we grade your project, you must include them in calc_autostereogram.s, lfsr_random.s, or quad2matrix.s. Changes you make to any other files will be overwritten when we grade your project.
The rest of the files are part of the framework. It may be helpful to look at all the other files.
autostereogram.s: The main program for calc_autostereogram. Links all of the files together.check.py: Runs sample tests against your programs.debug_random.s: A drop-in replacement for lfsr_random (see Debugging and Testing below).Makefile: We don't have to compile anything for this project. Not very useful.mars: A bash script that starts mars with command line options.Mars4_4.jar: The MIPS simulator we will be using.matrix.s: The main program for quad2matrix. Links all of the files together.print_helpers.s: Some helper functions to print values.print_matrix.s: A helper function that prints a 2D matrix of arbitrary size.quad2matrix_data.s: A test case for quad2matrix.random.s: The main program for lfsr_random. Links all of the files together.utils.s: Helper functions for the program.
Task A (Due 10/1)
Your first task will be to implement the autostereogram generator, like the examples in the introduction to Part 2. To implement the autostereogram generator, you first need to create a function that chooses pseudo-random numbers.
Your task
Edit the function in lfsr_random.s to implement the 16-bit LFSR from Lab 3, and edit the function in calc_autostereogram.s to implement the autostereogram algorithm using lfsr_random as a random number source.
Linear-Feedback Shift Register (LFSR) Pseudo Random Numbers Generator
Implement the 16-bit pseudo random number generator from lab 3, but now in MIPS. Your function must follow these specifications exactly. The solution in C has been made available for you. Note that this version performs the calculate-shift operation in a loop, 16 times in total. Your lab 3 code only performed one shift per function call, whereas this version will perform 16 shifts per function call. This is done in order to shift out all 16 old bits for 16 new bits.
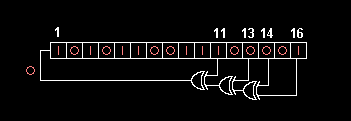
static uint16_t reg = 0x1;
for (int i = 0; i < 16; i++) {
uint16_t highest = ((reg >> 0) ^ (reg >> 2) ^ (reg >> 3) ^ (reg >> 5));
reg = (reg >> 1) | (highest << 15);
}
return reg;
There are no arguments for lfsr_random. You will use the .data section of lfsr_random.s to store your state. Your return value should be a 16-bit number (the upper 16 bits of $v0 should be 0).
Your output should match ours:
$ mars random.s
MARS 4.4 Copyright 2003-2013 Pete Sanderson and Kenneth Vollmar
26625
5185
27515
38801
56379
52819
14975
21116
38463
54726
38049
26552
4508
46916
37319
41728
23224
26004
11119
62850
Generating an autostereogram
The particular type of autostereogram we will be creating is known as a random dot autostereogram. To generate it, we need the above LFSR pseudo-random noise generator and a displacement map. The image below shows the depth map for the first autostereogram from the two examples above. In order for you to see it, we've scale up the intensity (the original depth map image is very dark).

Here is a link to a non-scaled depth map.
Let I(i,j) be the stereogram with width=M and height=N we would like to create using the displacement map, depth(i,j). Let S be the strip_size, which is always greater than the maximum displacement. The autostereogram I(i,j) can be calculated in the following way:

Again, in this description, the image has width=M and height=N. We say that I(i, j) is the image pixel at coordiates X=i, Y=j and depth(i, j) is the value of the depth map at X=i, Y=j. We define S to be our strip_size, which is a few columns of pixels on the left side of the image. As you can tell from the formula, we tile the "strip" and repeat it in the X direction throughout the rest of the image, with some small displacement. The random(A) function chooses a random value from the set A.
Autostereogram Generator
Once you have a working lfsr_random function, implement the calc_autostereogram function. Please follow these specifications exactly to make sure your program matches ours. (There are other ways to generate an autostereogram, but we will be grading your code based on these specifications.)
Arguments to calc_autostereogram:
- autostereogram - A pointer to an array of unsigned char. You will fill this in.
- depth_map - A pointer to an array of unsigned char. This is the depth() array in the autostereogram formula.
- width
- height
- strip_size
Some clarifications:
- Follow the autostereogram formula provided earlier to generate your autostereogram. Make sure your loop fills out the matrix column by column, as in the formula.
- The coordinate (0, 0) is at the top left of the image. The coordinate (M-1, 0) is at the top right. The coordinate (M-1, N-1) is at the bottom right.
- Columns 0 through S - 1 should have the value lfsr_random() & 0xff. Specifically:
- Ignore what the depth_map specifies for these columns.
- Use only the lower 8 bits, even though 16 random bits are generated with each call to our 16-bit number generator, lfsr_random().
- Columns S through M - 1 should have the value I((i + depth(i, j) - S), j) where i is the X coordinate and j is the Y coordinate of the current pixel.
- You do not need to handle values in the depth map that are less than 0.
- You do not need to handle values in the depth map that are greater than or equal to the strip size, S.
- You do not need to handle strip_sizes that are greater than the width of the image.
- You must call lfsr_random exactly strip_size × height times, and you must fill in the array one column at a time. Specifically:
- Use the first result of lfsr_random() in (0, 0). Then, in (0, 1). Then in (0, 2). Etc.
- After getting to …, (0, N-2), (0, N-1), you must move on to (1, 0).
Usage
Invoke the autostereogram generator with MARS, as follows.
$ mars autostereogram.s pa INPUT_FILE.bmp OUTPUT_FILE.bmp 16
MARS 4.4 Copyright 2003-2013 Pete Sanderson and Kenneth Vollmar
...
Here are some sample commands you can run to generate autostereograms:
$ ./mars autostereogram.s pa test/images/blob1-input.bmp test/output/blob1-output.bmp 50 ... $ ./mars autostereogram.s pa test/images/blob2-input.bmp test/output/blob2-output.bmp 47 ...
Add the --verbose option to the END of the arguments list to print out the depth_map and the resulting autostereogram. (Don't add it anywhere except the end.)
Task B (Due 10/1)
Your second task will be to take the quadtree you built in Part 1 of the project and turn it back into the row-major 1-D array (which represents a 2-D image matrix). Recall that our quadtrees are structured like this:
struct quadtree {
int leaf;
int size;
int x;
int y;
int gray_value;
qNode *child_NW, *child_NE, *child_SE, *child_SW;
};
Your task is to write the function in quad2matrix.s. It takes in a pointer to the root of a quadtree, a pointer to the first element of the matrix you will fill (already allocated for you), and the width of the matrix. Your function must traverse through the nodes of the tree and fill in the matrix with the correct values for each quadrant.
We have provided a print_matrix function that will be very useful to see the output matrix you are filling. The default data in quad2matrix_data.s is similar to the example quadtree we've used in the specs. The output for it should look like this:

Here are some tips:
- To run your program, type ./mars matrix.s.
- You are provided with the matrix (in the default file: 8 x 8; note this size may change so do not hard-code the value in your code) already, with all 0 values.
- Each element in the matrix is a byte (8 bits), not a word.
- Make sure to test your code against other sparse matrix. You can generate your own sparse matrix by following the format in quad2matrix_data.s.
- You can assume that non-leaf nodes have a gray_value of 256, and that leaf nodes will have a gray value that is between 0 and 255, inclusive.
- You can assume that leaf nodes have NULL (0) in their children pointers.
- You can assume that int leaf; is either 1 (leaf) or 0 (non-leaf).
Debugging and Testing
A testing framework and a few sample tests are provided for you. These tests are not a guarantee of the correctness of your code. Your code will be graded on its correctness, not whether or not it passes these tests. You can run the testing framework with make check. For lfsr_random and quad2matrix, the printed output is displayed on standard output. For calc_autostereogram, the output images and bytes will be written to test/output/TEST_NAME-output.bmp and test/output/TEST_NAME-output.txt.
$ make check
./check.py
Testing lfsr...
Running: ./mars random.s
Found: 26625
Found: 5185
...
...
All OK
You can also run the three programs using the bundled mars utility:
$ ./mars random.s ... $ ./mars matrix.s ... $ ./mars autostereogram.s mars autostereogram.s pa [input_file] [output_file] [strip_size] [--verbose] ...
Enabling program arguments in MARS Debugger
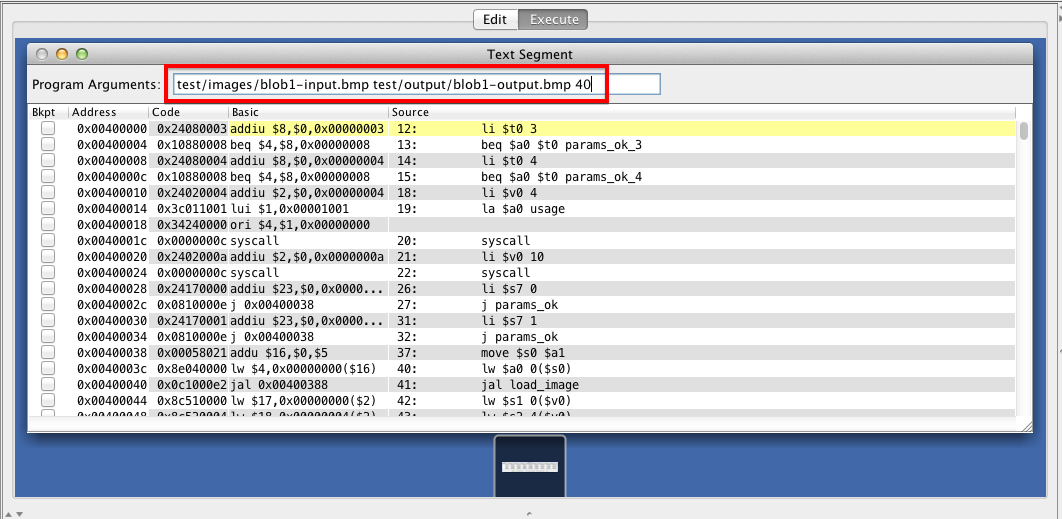
We use program arguments (argv) to pass input/output files and parameters to the autostereogram program. MARS lets you pass program arguments like this:
$ ./mars pa [ARGUMENT_1] [ARGUMENT_2] [...]
If you want to pass program arguments while running MARS in GUI mode, go to Settings → Program arguments provided to MIPS program and ensure it is enabled. Now, you can set MIPS program arguments. (Remember to omit the 'pa', which is a MARS keyword, not an argument to our program!)
Examining the heap in MARS
To store our images, we sometimes allocate memory on the heap (as in malloc). By default, MARS shows you the data segment of memory when you're debugging your code. You can switch to the heap segment by using the dropdown menu. (See below).
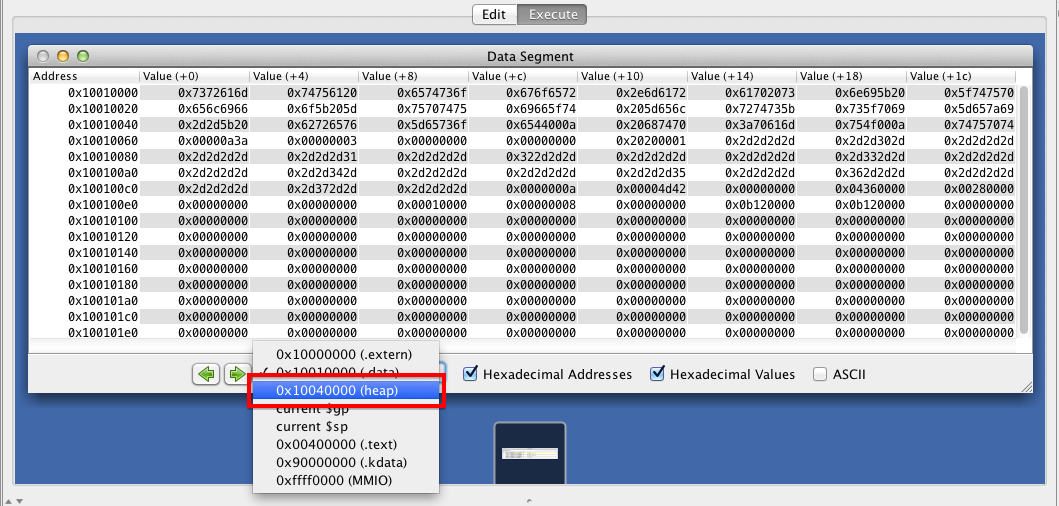
You can also use the green arrows (left and right) to move to other parts of memory. (You will need to do this in order to see where unsigned char *autostereogram is located!)
Running MARS over SSH
If you want to run a graphical program like MARS over SSH, you will need to set up X11 Forwarding for your SSH client.
- OS X users: Install XQuartz. Then start XQuartz and add the -X option to your ssh command. E.g. ssh -X cs61c-abc@hive1.cs.berkeley.edu.
- Windows users: Install Xming and PuTTY. Start Xming, then enable the Connection → SSH → X11 → Enable X11 Forwarding option. For more information and a step-by-step guide, read this article.
- Linux users: You should be able to enable X11 Forwarding by adding the -X option to your ssh command. E.g. ssh -X cs61c-abc@hive1.cs.berkeley.edu.
Once you are logged in with X11 Forwarding enabled, you can run ./mars & from the proj1-2 directory and MARS should start running.
Debugging autostereogram
Note: Before you start debugging calc_autostereogram.s, make sure your lfsr_random.s passes the check script!
The calc_autostereogram function is a little tricky to debug, but we have provided a couple of tools to help you out. First, there is a drop-in replacement for lfsr_random (which is hard to predict) which we've called debug_random1. This function returns 0xff every 3rd time that it's called, starting with the first time, and 0 otherwise. So, on a 8×2 grid, filling in ONE COLUMN AT A TIME from top-to-down left-to-right, you would get this:
(Note: colors are exaggerated)
| debug_random1 (strip_size=3) | |||||||
| ff | 00 | 00 | |||||
| 00 | ff | 00 | |||||
This is the depth map grid1-input.bmp, which is located at test/debug/grid1-input.bmp. Notice that there are 2 pixels with value 1 (displacement of 1) and everything else is 0 (no displacement).
| grid1-input.bmp | |||||||
| 00 | 00 | 00 | 00 | 00 | 01 | 00 | 00 |
| 00 | 00 | 00 | 00 | 01 | 00 | 00 | 00 |
Let's take strip_size = 3 and apply the autostereogram algorithm with debug_random1 and grid1-input.bmp. You should get this output: (if you can't figure out why, think about it for a while and do it by hand)
| grid1-expected.bmp | |||||||
| ff | 00 | 00 | ff | 00 | ff | ff | 00 |
| 00 | ff | 00 | 00 | 00 | 00 | 00 | 00 |
To run this test yourself, you will need to do the following:
- Change your call to lfsr_random in calc_autostereogram.s to debug_random1.
- Make sure you are filling in the array from left-to-right and up-to-down, where the COLUMN loop is the inner-most one.
- Make sure you are calling debug_random1 EXACTLY strip_size×height times.
- Run the command:
$ ./mars autostereogram.s pa test/debug/grid1-input.bmp test/output/grid1-output.bmp 3 --verbose MARS 4.4 Copyright 2003-2013 Pete Sanderson and Kenneth Vollmar Depth map: -----0----------1----------2----------3----------4----------5----------6----------7----- 0 0x00000000 0x00000000 0x00000000 0x00000000 0x00000000 0x00000001 0x00000000 0x00000000 1 0x00000000 0x00000000 0x00000000 0x00000000 0x00000001 0x00000000 0x00000000 0x00000000 Output: -----0----------1----------2----------3----------4----------5----------6----------7----- 0 0x000000ff 0x00000000 0x00000000 0x000000ff 0x00000000 0x000000ff 0x000000ff 0x00000000 1 0x00000000 0x000000ff 0x00000000 0x00000000 0x00000000 0x00000000 0x00000000 0x00000000 - Ensure that the output (the 2nd matrix) matches what is listed on this page.
- Change debug_random1 back to lfsr_random before submitting or using make check!
We have provided 4 total debugging grids designed to catch a variety of problems and help you debug in case your code doesn't work. They all depend on the same debug_random1 generator. Here are the commands and visualizations for all of the debug test grids:
Debug image: grid1
$ ./mars autostereogram.s pa test/debug/grid1-input.bmp test/output/grid1-output.bmp 3 --verbose
| debug_random1 (strip_size=3) | |||||||
| ff | 00 | 00 | |||||
| 00 | ff | 00 | |||||
| grid1-input.bmp | |||||||
| 00 | 00 | 00 | 00 | 00 | 01 | 00 | 00 |
| 00 | 00 | 00 | 00 | 01 | 00 | 00 | 00 |
| grid1-expected.bmp | |||||||
| ff | 00 | 00 | ff | 00 | ff | ff | 00 |
| 00 | ff | 00 | 00 | 00 | 00 | 00 | 00 |
Debug image: grid2
$ ./mars autostereogram.s pa test/debug/grid2-input.bmp test/output/grid2-output.bmp 3 --verbose
| debug_random1 (strip_size=3) | |||||||
| ff | 00 | 00 | |||||
| 00 | 00 | ff | |||||
| 00 | ff | 00 | |||||
| ff | 00 | 00 | |||||
| grid1-input.bmp | |||||||
| 00 | 00 | 00 | 01 | 00 | 00 | 00 | 00 |
| 00 | 00 | 00 | 00 | 00 | 01 | 00 | 00 |
| 00 | 00 | 00 | 00 | 01 | 00 | 00 | 00 |
| 00 | 00 | 00 | 01 | 00 | 00 | 00 | 00 |
| grid1-expected.bmp | |||||||
| ff | 00 | 00 | 00 | 00 | 00 | 00 | 00 |
| 00 | 00 | ff | 00 | 00 | 00 | 00 | 00 |
| 00 | ff | 00 | 00 | 00 | 00 | 00 | 00 |
| ff | 00 | 00 | 00 | 00 | 00 | 00 | 00 |
Debug image: grid3
$ ./mars autostereogram.s pa test/debug/grid3-input.bmp test/output/grid3-output.bmp 3 --verbose
| debug_random1 (strip_size=3) | |||||||
| ff | 00 | 00 | |||||
| 00 | ff | 00 | |||||
| grid3-input.bmp | |||||||
| 00 | 00 | 00 | 00 | 02 | 01 | 00 | 00 |
| 00 | 00 | 00 | 01 | 00 | 01 | 02 | 00 |
| grid3-output.bmp | |||||||
| ff | 00 | 00 | ff | ff | ff | ff | ff |
| 00 | ff | 00 | ff | ff | ff | ff | ff |
Debug image: grid4 (Note: strip_size has changed to 4 for this one)
$ ./mars autostereogram.s pa test/debug/grid4-input.bmp test/output/grid4-output.bmp 4 --verbose
| debug_random1 (strip_size=4) | ||||||
| ff | 00 | 00 | ff | |||
| 00 | ff | 00 | 00 | |||
| 00 | 00 | ff | 00 | |||
| ff | 00 | 00 | ff | |||
| 00 | ff | 00 | 00 | |||
| grid4-input.bmp | ||||||
| 00 | 00 | 00 | 00 | 02 | 02 | 01 |
| 00 | 00 | 00 | 00 | 01 | 01 | 02 |
| 00 | 00 | 00 | 00 | 02 | 03 | 01 |
| 00 | 00 | 00 | 00 | 01 | 02 | 03 |
| 00 | 00 | 00 | 00 | 01 | 02 | 02 |
| grid4-output.bmp | ||||||
| ff | 00 | 00 | ff | 00 | ff | ff |
| 00 | ff | 00 | 00 | ff | 00 | ff |
| 00 | 00 | ff | 00 | ff | ff | 00 |
| ff | 00 | 00 | ff | 00 | ff | ff |
| 00 | ff | 00 | 00 | ff | 00 | ff |
Submission
The full proj1-2 is due Wednesday, 10/1. To submit the full proj1-2, enter in the following. You should be turning in calc_autostereogram.s, lfsr_random.s, and quad2matrix.s.
$ cd ~/proj1-2 $ submit proj1-2