CS61C Fall 2014 Project 2: MapReduce

TA: Shreyas Chand, Alex Chou, Jay Patel
Part 1: Due 10/27 @ 23:59:59
Part 2: Due 11/02 @ 23:59:59

Updates

All updates to the project spec will be listed in this section.

Clarifications/Reminders

Table of Contents

Goals

The goal of this project is to get you familiar with the MapReduce programming model using the Apache Spark framework. The first part of the project will give you an opportunity to turn breadth-first traversal (an algorithm with which you're hopefully already familiar) into a format that is compatible with the MapReduce framework. The second part will require you to run your implementation on a large cluster of Amazon Web Services Elastic Compute Cloud (AWS EC2) servers in order to crunch through a large problem. We hope that by doing this project you will gain an appreciation for the MapReduce programming model, and at the same time pick up a very marketable skill.

Part 1 (Due 10/27 @ 23:59:59)

Background

Strongly Solving Puzzles

One-player, reversible puzzles are lots of fun; popular examples you may have played yourself include Rubik's™ cube and sliding puzzles, like Rush Hour, Klotski and the Fifteen puzzle. These puzzles have the property that you can get from any position (a particular unique configuration of the puzzle) to another; there are no "dead ends". In this project, you will write a breadth-first solver that starts from the single solution position, and walks the graph, recording every new position it reaches (and how many moves it took to get there, we call that the level). Unlike breadth-first search, in which you stop when you've found a particular position, here you're going to exhaustively visit the entire graph (this is called strongly solving). To do this, we keep track of two mappings (which in Python, are dictionaries):

For the purpose of this project, we are going to be solving the generalized Fifteen puzzle (Width x Height), but we'll give you all the code you need for this particular game. With a smaller puzzle (small values of Width and Height), it should also be easier for you to verify the correctness of your output. Of course, you can try larger parameters if you have enough time, and space on your hard drive.

Breadth-First Solver

Here is our generic breadth-first solver in Python. It takes in a puzzle, and a max_level as arguments. The parameter max_level is used to control how far the solver should solve (if it's left out, or set to -1, the solver will visit every position in the puzzle graph). Here, the parameter puzzle is an object with two important methods:

level_to_pos = {}
pos_to_level = {}

def solve(puzzle, max_level=-1):
    """BF visit the entire puzzle graph, build level_to_pos, pos_to_level structures."""
    solution = puzzle.solution()
    level = 0
    level_to_pos[level] = [solution] ### level 0 consists of a single solution 
    pos_to_level[solution] = level

    ### While there are still positions on the frontier
    ### (seen for the first time in the last iteration)
    while level_to_pos[level] and (max_level==-1 or level < max_level):
        level += 1
        level_to_pos[level] = []
        ### For every position on the last level (these farthest-away positions are the "frontier")
        for position in level_to_pos[level-1]:
            ### For every child of those frontier positions
            for child in position.children():
                ### If it's the first time we've seen this child
                if child not in pos_to_level:
                    ### Update the mappings to remember it, and it will be part of the new frontier
                    pos_to_level[child] = level
                    level_to_pos[level].append(child)

    del level_to_pos[level] ### the last level is always empty, so remove it.

Example using the 3- and 5-gallon "Die Hard 3" puzzle

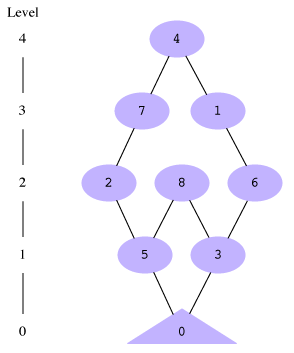
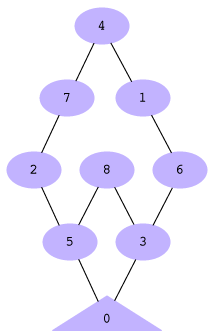Diehard53 Puzzle Imagine you have a number (between 0 and 8, inclusive) that you can increase or decrease by 3 or 5, as long as it never gets below 0 or above 8. The goal of the game is to get to 0. This is the opposite of the "Die Hard 3" puzzle where the goal was to start at 0 and fill and empty 3- and 5-gallon jugs to get to 4. The overall game graph is shown on the left; you might take a second to convince yourself that this is every position that exists, and that the edges connecting positions are the only connections between positions that are possible:

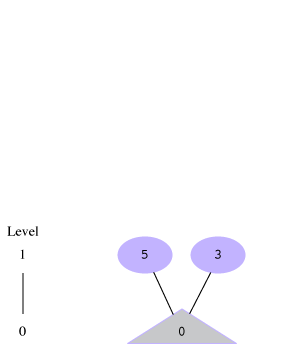
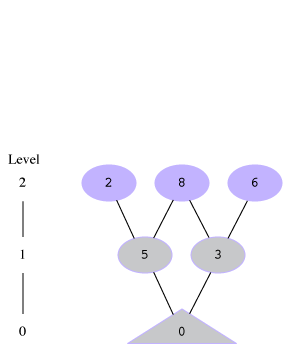
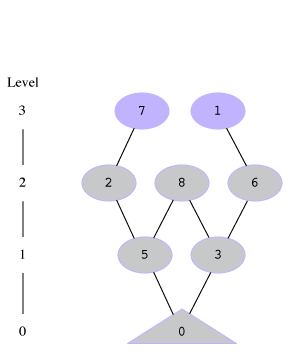
If we run our breadth-first solver algorithm on this, here's what would happen. Note that during the last level=5 iteration, it visits all the children of the frontier [4] and finds 7 and 1, but they've both been seen before, so there are no new positions added to the frontier, and the next iteration breaks out of the while loop.

  level = 0, before while Known graph so far After level = 1 Known graph so far After level = 2 Known graph so far After level = 3 Known graph so far After level = 4 Final graph
level_to_pos[0] [0] Diehard53 Puzzle [0] Diehard53 Puzzle [0] Diehard53 Puzzle [0] Diehard53 Puzzle [0] Diehard53 Puzzle
level_to_pos[1] [5, 3] [5, 3] [5, 3] [5, 3]
level_to_pos[2] [2, 8, 6] [2, 8, 6] [2, 8, 6]
level_to_pos[3] [7, 1] [7, 1]
level_to_pos[4] [4]
pos_to_level[0] 0 0 0 0 0
pos_to_level[1] 3 3
pos_to_level[2] 2 2 2
pos_to_level[3] 1 1 1 1
pos_to_level[4] 4
pos_to_level[5] 1 1 1 1
pos_to_level[6] 2 2 2
pos_to_level[7] 3 3
pos_to_level[8] 2 2 2

Getting started

As mentioned above, we are going to be solving the generalized Fifteen puzzle, which we call the Sliding puzzle (with input parameters width and height). This puzzle consists of numbered tiles in a random ordering with one tile missing. The objective of the game to place the tiles in order as shown in the image below, for the 3x3 case.

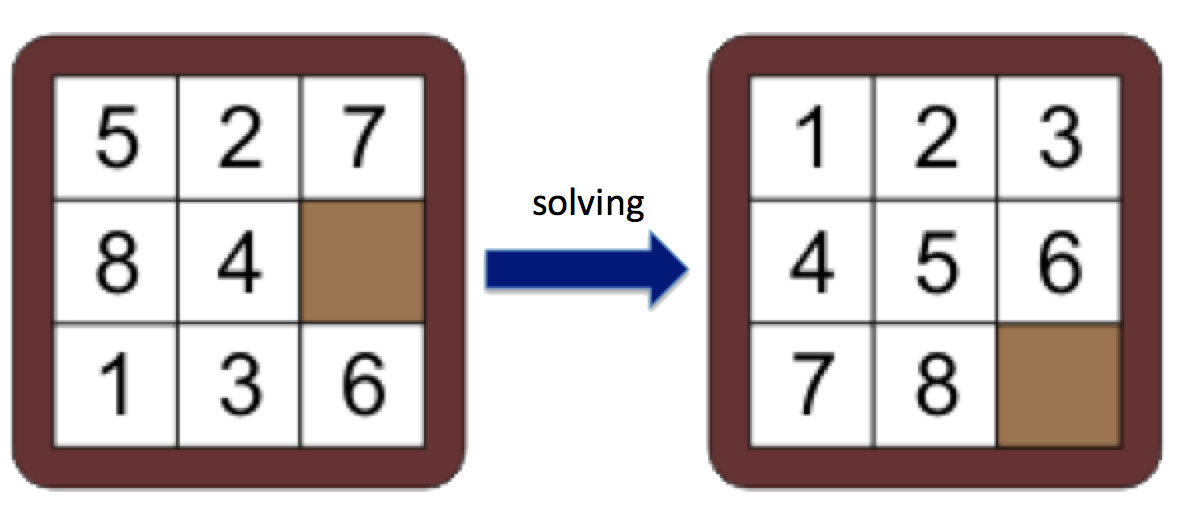
If you've never played the game before, it might be helpful (and fun!) to try it here. That website allows you to play a 3x3, 4x4, or 5x5 puzzle.

Starter Code

To get started on the project, copy the files in the directory ~cs61c/proj/02 to your proj2 directory, by entering the following command:

$ cp -r ~cs61c/proj/02 ~/proj2

The file you will need to modify and submit is:

You are free (and encouraged) to define and implement additional helper functions, but they must be in SlidingBfsSpark.py. Changes you make to any other files will be overwritten when we grade your project.

The rest of the files are part of the framework and should not be modified. However, you will need to look at them as well.

Your Job

Your task will be to implement an iterative MapReduce job to solve the general Sliding puzzle.

As described above, this MapReduce job will take as input a width and height describing a Sliding puzzle. Using the solution, it will repeatedly expand the BFS tree, and generate a mapping between every position and the level at which it is in the BFS tree.

We represent a Sliding puzzle as a Python tuple of strings. Each tile is an alphabetic character and the empty space is represented with a hyphen '-'.

Therefore, after running your MapReduce job, we expect your program to produce a text file of the following form. (for example, for a 2x2 case):

0 ('A', 'B', 'C', '-')
1 ('A', '-', 'C', 'B')
1 ('A', 'B', '-', 'C')
2 ('-', 'A', 'C', 'B')
2 ('-', 'B', 'A', 'C')
3 ('B', '-', 'A', 'C')
3 ('C', 'A', '-', 'B')
4 ('B', 'C', 'A', '-')
4 ('C', 'A', 'B', '-')
5 ('B', 'C', '-', 'A')
5 ('C', '-', 'B', 'A')
6 ('-', 'C', 'B', 'A')

Your output is not required to be sorted by level as ours is, but you might find it helpful for debugging. If it is sorted, you could use a utility such as diff (or vimdiff) to easily catch any errors. If you have never used diff before, this article does a good job of explaining its usage along with great examples.

Here's a recommended plan of attack:

Follow Up Questions to Submit

You will submit you and your partners answers to the following questions in proj2-1.txt.

1. Some games (e.g., Rush Hour, Klotski, etc.) do not have a single solution, but a set of solution positions (and a single starting position). This is because those puzzles only care about the final position of a particular block, and don't care about the location of the other blocks. In terms of an API change, solution() wouldn't be a no-argument function that returns the single solution position anymore, but instead be a predicate that took in a position and returned whether it was in the solution set or not. Your friend suggests to generate all the permutations of blocks (or whatever else is being moved / rotated / changed in the puzzle) that satisfy the solution predicate, call them all solutions (level = 0), and proceed normally.

1 2
3 -
For example, let's say a 2x2 puzzle is considered to be solved when "1", in the upper left slot (and the position of the other positions doesn't matter). So the friend is suggesting to put "1" in the upper left, then write custom code to permute "(2,3,-)" around all the other positions, create positions for all of those permutations, declare all of those positions as solutions, and proceed to strongly solve.

What is one potential problem with this idea? (Hint: take a look at the number of positions in the 2x2 final solution and compare that with all the ways of permuting four pieces).

2. What's a better algorithm to solve these kinds of puzzles? How would you modify your original solver?

3. On the same note, what needs to be changed to solve loop-free puzzles, like Peg Solitaire. For every position, rather than the distance to the solution, what might you store? What changes would you make to your solver? In the case of Peg Solitaire, would it change the memory requirements of your solver?

Debugging and Testing

You should test your code on one of the following servers. (See below for benchmark information).

The provided Makefile gives you the ability to run your solver on a few common cases. Be sure to understand all of the "targets" provided to you in the Makefile. For example:

$ make run-small # Runs your solver with a Sliding puzzle of size 2x2

In the ref_out directory, we have also provided you with the correct output and format we expect for the 2x2 Sliding puzzle. You can use this small case as a basic sanity check and to verify that your output format is correct.

While you are working on the project, we encourage you to keep your code under version control. However, if you are using a hosted repository (i.e. GitHub, BitBucket, etc), it MUST be private. If we find any public repositories, it will be viewed as a violation of academic integrity and therefore an automatic F in the course. We refer you to the full cheating policy here.

If you mistakenly break parts of the skeleton, you can always grab a new copy of the file by running the following command, but BE VERY CAREFUL not to overwrite all your work. 

$ cp ~cs61c/proj/02/<NAME OF FILE> ~/proj2

Before you submit, make sure you test your code on the Hive machines. We will be grading your code there. IF YOUR PROGRAM THROWS AN EXCEPTION/ERROR WHICH COULD HAVE BEEN REVEALED BY SIMPLE TESTING, YOU WILL AUTOMATICALLY GET A ZERO FOR THAT PORTION OF THE ASSIGNMENT. There is no excuse not to test your code.

Grading

Other Grading Notes

Keep in mind that your running time is highly dependent on who else is logged into the server you are using and what they are running. You can use the who, w, and top commands to get a sense of what other users and processes are sharing your machine, and whether you should try another one.

Submission

proj2-1 is due Monday (10/27/2014). To submit proj2-1, use the following commands. You should just be turning in SlidingBfsSpark.py and proj2-1.txt. 

$ cd ~/proj2
$ submit proj2-1

Notes On Spark

We highly recommend you read and understand this short Spark programming guide, especially the section on key-value pairs and their transformations. After all, if you choose to put Apache Spark on your résumé, you want to be able to answer any questions that are thrown your way ;).

Finally, the other resource that will come in handy is the detailed Spark-Python API, available at: http://spark.apache.org/docs/latest/api/python/pyspark-module.html

Global Variables

In the lab, we mentioned global variables should be avoided in Spark. This isn't entirely true - let us elaborate on this a bit more. Global variables may cause poor performance because they require information to be shared among the nodes in your cluster. If this global variable is frequently being changed, this data must frequently be copied to and from nodes, which hurts parallelism. However, if your global variable is simply a read-only constant, (for example, the width and height of the board), that is fine.

If you have some information that is to be shared and processed by all the nodes in parallel, you should be using an RDD (resilient distributed dataset), the primary abstraction in Spark.

For the curious, Spark provides other abstractions for shared variables, namely broadcast variables and accumulators. Our solution does not make use of these, but you are free to try them if you wish.

Advanced Notes

After getting a basic solution working, use these techniques to further optimize your performance.

Lazy Evaluation

As you should understand from reading the Spark docs, transformations on RDDs in Spark are lazy (remember lazy evaluation from 61A?). The result is only computed when it is required by some action, such as count or saveAsTextFile.

You may find that you achieve better performance by not "materializing" your RDD for each iteration of your MapReduce job -- that is, you may allow several iterations of transformations to occur before calling an action on it. Spark is able to optimize the collection of transformations better than each transformation individually.

Partitioning

An RDD is a collection of elements partitioned across nodes in a cluster. By default, Spark simply splits up the RDD into sequential partitions and ships them off to individual nodes. When it is time to reduce, KV pairs may need to be shipped across nodes in the shuffling phase. Because shuffling requires moving data around (sometimes over a network), it is a comparatively expensive operation.

You may find that you can achieve better performance by partitioning your dataset in a more intelligent way. This allows some of the reducing to take place locally on a particular node, rather than requiring it to be shuffled. See the partitionBy operation on RDDs for more info.

As a final note, since repartitioning itself requires reshuffling large chunks of the data, it may be useful to not repartition on every iteration, but rather every k iterations, where you decide what k is.