Clarifications/Reminders
- Start Early!
- This project should be done on either the hive machines. Parts of your program may not work on other computers.
- This project is to be completed individually.
- Make sure you read through the project spec before starting.
Goals
This project will expose you to C and RISC-V in greater depth. The first part gives you the opportunity to sharpen your C programming skills that you have learned in the past few weeks, while the second part dives deeper into coding. Part of this project will also serve as the basis for the upcoming project 2. In particular part 1's goals are:
- To give you practice applying algorithms in C.
- To give you more experience doing memory management in C.
- To expose you to helpful C testing tools like CUnit and Valgrind.
- For you to have fun.
Background
Cameras traditionally capture a two dimensional projection of a scene. However depth information is important for many real-world application including robotic navigation, face recognition, gesture or pose recognition, 3D scanning, and self-driving cars. The human visual system can preceive depth by comparing the images captured by our two eyes. This is called stereo vision. In this project we will experiment with a simple computer vision/image processing technique, called "shape from stereo" that, much like humans do, computes the depth information from stereo images (images taken from two locations that are displaced by a certain amount).
Depth Perception
Humans can tell how far away an object is by comparing the position of the object is in left eye's image with respect to right eye's image. If an object is really close to you, your left eye will see the object further to the right, whereas your right eye will see the object to the left. A similar effect will occur with cameras that are offset with respect to each other as seen below.
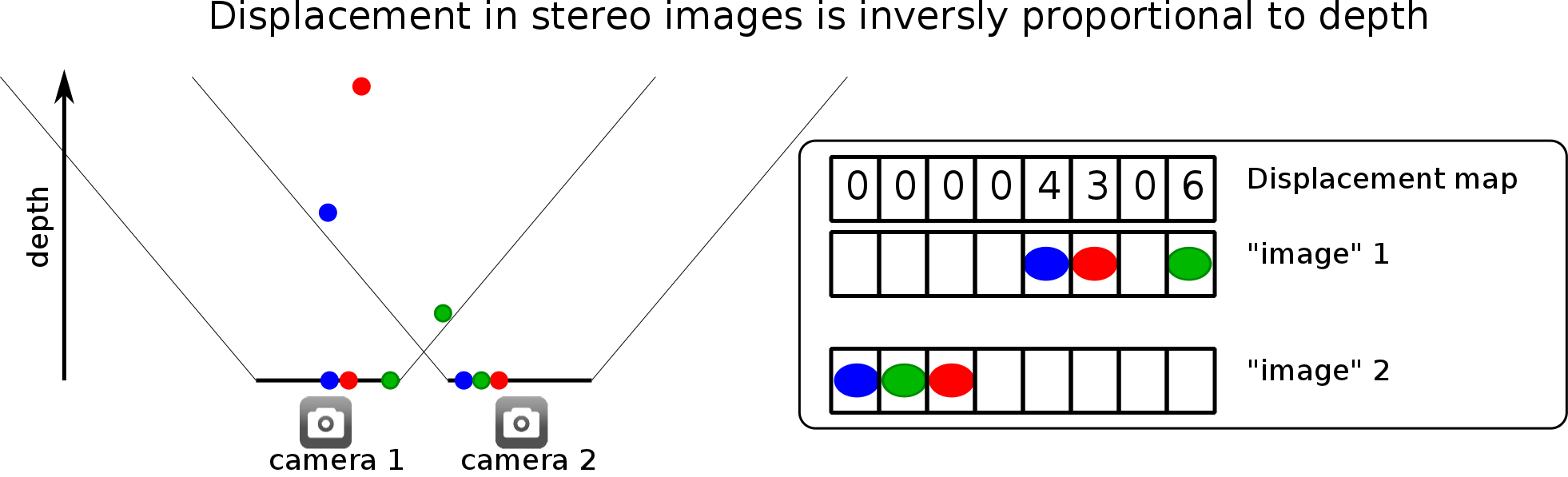
The above illustration shows 3 objects at different depth and position. It also shows the position in which the objects are projected into image in camera 1 and camera 2. As you can see, the closest object (green) is displaced the most (6 pixels) from image 1 to image 2. The furthest object (red) is displaced the least (3 pixels). We can therefore assign a displacement value for each pixel in image 1. The array of displacements is called displacement map. The figure shows the displacement map corresponding to image 1.
Your task will be to find the displacement map using a simple block matching algorithm. Since images are two dimensional we need to explain how images are represented before going to describe the algorithm.
Below is a classic example of left-right stereo images and the displacement map shown as an image.

Part 1 (Due 9/18 @ 23:59:59)
Objective
In this project, we will attempting to simulate depth perception on the computer, by writing a program that can distinguish far away and close by objects.
Getting started
First, create a Project 1 GitHub Classroom repository. Make sure to add https://github.com/61c-teach/fa18-proj1-starter.git as the remote as you've did for the homework and lab repositories.
The files you will need to modify and submit are:
calc_depth.c: Creates a depth map out of two images. You will be implementing thecalc_depth()function.make_qtree.c: Creates a quadtree representation from a depth map. You will be implementing thedepth_to_quad(),homogenous()andfree_qtree()functions.
You are free to define and implement additional helper functions, but if you want them to be run when we grade your project, you must include them in calc_depth.c or make_qtree.c. Changes you make to any other files will be overwritten when we grade your project.
The rest of the files are part of the framework. It may be helpful to look at all the other files.
Makefile: Defines all the compilation commands.depth_map.c: Loads bitmap images and calls the calc_depth() to calculate the depth map.calc_depth.h: Defines the signature for the calc_depth() function you will implement.make_qtree.h: Defines the signature for the depth_to_quad() and homogenous() functions you will implement.quadtree.h: Defines the qNode struct, as well as quadtree.c function headers.quadtree.c: Calls depth_to_quad() and free_qtree().utils.h: Defines Image struct and utility function signatures.utils.c: Defines bitmap loading, printing, and saving functions.test/: Contains the files necessary for testing. images/ holds input images, output will contain output files created by the program, and expected/ has the correct output of the tests. cunit contains code to help with unit testing.
Task A (Due 9/18)
Your first task will be to implement the depth map generator. This function takes two input images (unsigned char *left and unsigned char *right), which represent what you see with your left and right eye, and generates a depth map using the output buffer we allocate for you (unsigned char *depth_map).
Generating a depth map
In order to achieve depth perception, we will be creating a depth map. The depth map will be a new image (same size as left and right) where each "pixel" is a value from 0 to 255 inclusive, representing how far away the object at that pixel is. In this case, 0 means infinity, while 255 means as close as can be. Consider the following illustration:

The first step is to take a small patch (here 5x5) around the green pixel. This patch is represented by the red rectangle. We call this patch a feature. To find the displacement, we would like to find the corresponding feature position in the other image. We can do that by comparing similarly sized features in the other image and choosing the one that is the most similar. Of course, comparing against all possible patches would be very time consuming. We are going to assume that there's a limit to how much a feature can be displaced -- this defines a search space which is represented by the large green rectangle (here 11x11). Notice that, even though our images are named left and right, our search space extends in both the left/right and the up/down directions. Since we search over a region, if the "left image" is actually the right and the "right image" is actually the left, proper distance maps should still be generated.
The feature (a corner of a white box) was found at the position indicated by the blue square in the right image.
We'll say that two features are similar if they have a small Squared Euclidean Distance. If we're comparing two features, A and B, that have a width of W and height of H, their Squared Euclidean Distance is given by:

(Note that this is always a positive number.)
For example, given two sets of two 2×2 images below:
 ← Squared Euclidean distance is (1-1)2+(5-5)2+(4-4)2+(6-6)2 = 0 →
← Squared Euclidean distance is (1-1)2+(5-5)2+(4-4)2+(6-6)2 = 0 →
 ← Squared Euclidean distance is (1-3)2+(5-5)2+(4-4)2+(6-6)2 = 4 →
← Squared Euclidean distance is (1-3)2+(5-5)2+(4-4)2+(6-6)2 = 4 →
(Source: http://cybertron.cg.tu-berlin.de/pdci08/imageflight/descriptors.html)
Once we find the feature in the right image that's most similar, we check how far away from the original feature it is, and that tells us how close by or far away the object is.
Definitions (Inputs)
We define these variables to your function:
- image_width
- image_height
- feature_width
- feature_height
- maximum_displacement
We define the variables feature_width and feature_height which result in
feature patches of size: (2 × feature_width + 1) × (2 × feature_height + 1). In the
previous example, feature_width = feature_height = 2 which gives a 5×5 patch. We also define the variable
maximum_displacement which limits the search space. In the previous example maximum_displacement = 3 which
results in searching over (2 × maximum_displacement + 1)2 patches in the second image to compare with.
Definitions (Output)
In order for our results to fit within the range of a unsigned char, we output the normalized displacement between the left feature and the corresponding right feature, rather than the absolute displacement. The normalized displacement is given by:
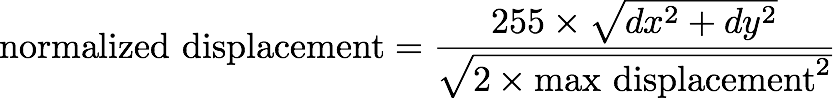
This function is implemented for you in calc_depth.c.
In the case of the above example, dy=1 and dx=2 are the vertical and horizontal displacement of the green pixel. This formula will guarantee that we have a value that fits in a unsigned char, so the normalized displacement is 255 × sqrt(1 + 22)/sqrt(2 × 32) = 134, truncated to an integer.
Bitmap Images
We will be working with 8-bit grayscale bitmap images. In this file format, each pixel takes on a value between 0 and 255 inclusive,
where 0 = black, 255 = white, and values in between to various shades of gray. Together, the pixels
form a 2D matrix with image_height rows and image_width columns.
Since each pixel may be one of 256 values, we can represent an image in memory using an array of unsigned char of size
image_width * image_height. We store the 2D image in a 1D array such that each row of the image occupies a contiguous
part of the array. The pixels are stored from top-to-bottom and left-to-right (see illustration below):
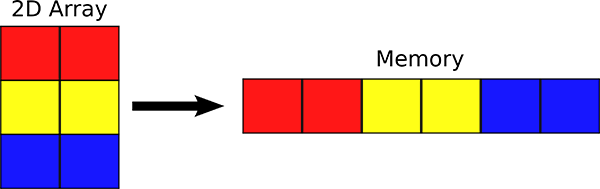
(Source: http://cnx.org/content/m32159/1.4/rowMajor.png)
We can refer to individual pixels of the array by specifying the row and column it's located in. Recall that in a matrix,
rows and columns are numbered from the top left. We will follow this numbering scheme as well, so the leftmost red square
is at row 0, column 0, and the rightmost blue square is at row 2, column 1. In this project, we will also refer to an element's
column # as its x position, and it's row # as its y position. We can also call the # of columns of the image
as its image_width, and the # of rows of the image as its image_height. Thus, the image above has a width of 2, height of 3,
and the element at x=1 and y=2 is the rightmost blue square.
Your task
Edit the function in calc_depth.c so that it generates a depth map and stores it in unsigned char *depth_map, which points to a pre-allocated buffer of size image_width × image_height. Two images, left and right are provided. They are also of size image_width × image_height. The feature_width and feature_height parameters are described in the Generating a depth map section.
Here are some implementation details and tips:
- A feature is a box of width
2 × feature_width + 1and height2 × feature_height + 1, with the original position of the pixel at its center. - You may not assume
feature_height=feature_width=maximum_displacement. They may all be different (e.g. your feature box may be a rectangle). - Pixels on the edge of the image, whose left-image features don't fit inside the image, should have a normalized displacement of 0 (infinite).
- When
maximum_displacementis 0, the whole image would have a normalized displacement of 0. - Your algorithm should not consider right-image features that lie partially outside the image area. However, if the left-image feature of a pixel is fully within the image area, you should always be able to assign a normalized displacement to that pixel.
- The source pixels always come from
unsigned char *left, whereas theunsigned char *rightimage is always the one that is scanned for nearby features. - You may not assume that
unsigned char *depth_maphas been filled with zeros. - You may not store global variables that persist between multiple calls to
calc_depth. - The Squared Euclidean Distance should be calculated according to the formula:

- After finding the matching feature in the right image with the smallest Squared Euclidean Distance, the normalized displacement of the pixel is given by the formula:
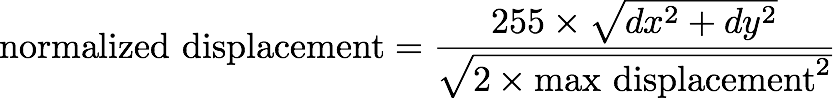
- Ties in the Euclidean Distance should be won by the one with the smallest resulting normalized displacement.
- Some test cases are provided by
make check. These are not all of the tests that we will be grading your project on.
Usage
Use make to compile the calc_depth. Your code must compile with the given Makefile:
$ make
gcc -Wall -g -std=c99 -o ....
....
You can now run ./depth_map to see the options that the program takes.
$ ./depth_map
USAGE: ./depth_map [options]
REQUIRED
-l [LEFT_IMAGE] The left image
-r [RIGHT_IMAGE] The right image
-w [WIDTH_PIXELS] The width of the smallest feature
-h [HEIGHT_PIXELS] The height of the smallest feature
-t [MAX_DISPLACE] The threshold for maximum displacement
OPTIONAL
-o [OUTPUT_IMAGE] Draw output to this file
-v Print the output to stdout as readable bytes
The -o option will let you visualize your depth map as a BMP image that you can open in your file browser. In these images, blue regions are far away and red regions are close by.
A testing framework and a few sample tests are provided for you. These tests are not a guarantee of the correctness of your code. Your code will be graded on its correctness, not whether or not it passes these tests. You can run the testing framework with make check. For calc_depth, the output images and bytes will be written to test/output/TEST_NAME-output.bmp and test/output/TEST_NAME-output.txt. For quadtree, the printed output is written to test/output/TEST_NAME-output.txt.
You can use your own 8-bit grayscale BMP images to test your code. There are helper functions in utils.c to generate BMP files from unsigned char arrays. Alternatively, you can generate them with an image editing program like Photoshop.
$ ./depth_map -l test/images/quilt2-left.bmp -r test/images/quilt2-right.bmp -h 0 -w 0 -t 1 -o test/output/quilt2-output.bmp -v
00 00 00
00 ff 00
00 00 b4
Advice
- Try to think about how to marginalize the problem before starting. How do you select the closest portion of a picture? How do you evaluate how close two feature spaces are? How do you determine the distance between two pixels?
- If you get stuck try testing a portion with the CUnit tests (see the testing section below).
- Step through the unit tests in cgdb rather than a whole program.
- If you find yourself stuck or not passing tests doublecheck what the spec asks you to do. It impossible to write effective tests if you get the expected results wrong.
Task B (Due 9/18)
Your second task will be to implement quadtree compression. This function takes a depth map (unsigned char *depth), and generates a recursive data structure called a quad tree.
Quadtree Compression
The depth maps that we create in this project are just 2D arrays of unsigned char. When we interpret each value as a square pixel, we can output a rectangular image. We used bitmaps in this project, but it would be incredibly space inefficient if every image on the internet were stored this way, since bitmaps store the value of every pixel separately. Instead, there are many ways to compress images (ways to store the same image information with a smaller filesize). In task B, you will be asked to implement one type of compression using a data structure called a quadtree.
A quadtree is similar to a binary tree, except each node must have either 0 children or 4 children. When applied to a square bitmap image whose width and height can be expressed as 2N, the root node of the tree represents the entire image. Each node of the tree represents a square sub-region within the image. We say that a square region is homogenous if its pixels all have the same value. If a square region is not homogenous, then we divide the region into four quadrants, each of which is represented by a child of the quadtree parent node. If the square region is homogeneous, then the quadtree node has no children and instead, has a value equal to the color of the pixels in that region.
We continue checking for homogeneity of the image sections represented by each node until all quadtree nodes contain only pixels of a single grayscale value. Each leaf node in the quadtree is associated with a square section of the image and a particular grayscale value. Any non-leaf node will have a value of -1 (outside the grayscale range) associated with it, and should have 4 child nodes.
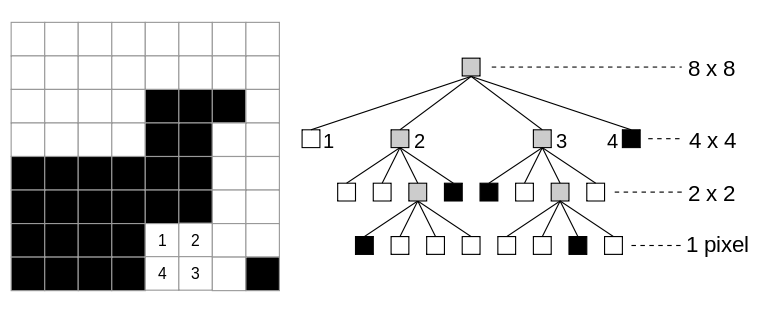
(Source: http://en.wikipedia.org/wiki/File:Quad_tree_bitmap.svg)
We will be numbering each child node created (1-4) clockwise from the top left square, as well with their ordinal direction (NW, NE, SE, SW). When parsing through nodes, we will use this order: 1: NW, 2: NE, 3: SE, 4: SW.
Given a quadtree, we can choose to only keep the leaf nodes and use this to represent the original image. Because the leaf nodes should contain every color value represented, the non-leaf nodes are not needed to reconstruct the image. This compression technique works well if an image has large regions with the same grayscale value (artificial images), versus images with lots of random noise (real images). Depth maps are a relatively good input, since we get large regions with similar depths.
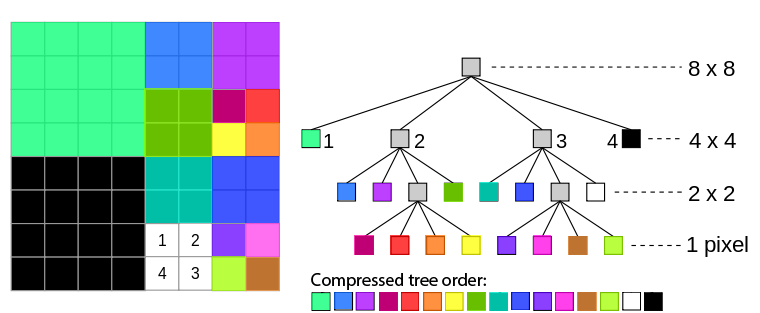
Your Job
Your task is to write the depth_to_quad(), homogenous() and free_qtree() functions located in make_qtree.c.
The first function, depth_to_quad() takes an array of unsigned char, converts it into a quadtree, and returns a
pointer to the root qNode in the tree. Keep in mind that local variables don't last after your function returns, so you must use
dynamic memory allocation in the function. Since memory allocation could fail, you need to check whether the pointer
returned by malloc() is valid or not. If it is NULL, you should call allocation_failed() (defined in utils.h).
Your representation should use a tree of qNodes, all of which either have 0 or 4 children. The declaration of the struct qNode is in quadtree.h.
The second function homogenous() takes in the depth_map as well as a region of the image (top left coordinates, width, and height). If every pixel in that region has the same grayscale value, then homogenous() should return that value. Or else, if the section is non-homogenous, it should return -1.
The third function free_qtree() should take in the root of a qtree and should free all the memory associated with that tree. Since any node is itself the root of a subtree the root passed in just needs to be a malloced node, not the necessarily the root of the original tree.
Here are a few key points regarding your quadtree representation:
- Leaves should have the boolean value leaf set to
true, while all other nodes should have it asfalse. - The gray_value of leaves should be set to their grayscale value, but non-leaves should take on the value -1.
- The x and y variables should hold the top-left pixel coordinate of the image section the node represents.
- We only require that your code works with images that have widths that are powers of two. This means that all qNode sizes will also be powers of two and the smallest qNode size will be one pixel.
- The four child nodes are marked with ordinal directions (NW, NE, SE, SW), which you should match closely to the corresponding sections of the image.
- Some test cases are provided by
make check. These are not all of the tests that we will be grading your project on. - Don't worry about NULL images or images of size zero, we won't test for these (but you're welcome to have a check for it anyways and return null)
- Your final code needs to have no memory leaks. Make sure your free_qtree() free the entire subtree associated with a root.
- Your may not assume that the pointer passed in to free_qtree() is not NULL.
The following example illustrates these points:
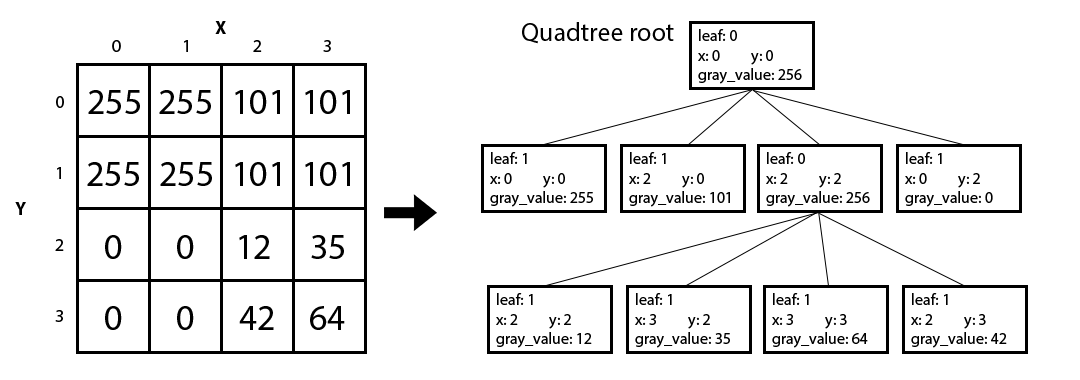
You can compile your code for task B with the following command:
$ make quadtree
Running the program with no arguments will print out the quadtree and compressed representation for a few arrays defined in print_basic(). You can also pass in the name of a grayscale bitmap image, and the code will compress the image and print out the quadtree and compressed representations (although we have not included any tests). Note that for any images whose dimensions are not square powers of two, the program will grab a square section at the approximate center of the image.
Advice
- Try segmenting the problem. First construct the quadtree and then try including compression.
- If you find yourself stuck add CUnit tests (see testing).
- Run valgrind to make sure your code has no memory leaks. You should figure out how to do this from task C.
Task C (due 9/18)
The final task is a small exercise intended to teach you have to use valgrind. From lecture and lab you should have seen that memory that is allocated and not freed results in a memory leak. One particularly useful piece of software for detecting memory leaks is valgrind and it is already installed on the hive. If you learn how to use valgrind you can quickly detect many memory errors that occur (not just memory leaks). Unfortunately many students do not realize how powerful valgrind can be and so this exercise is intended to assist you in learning to use valgrind and to approach documentation in general. In the depth_map program there exists exactly 1 memory leak in the starter code. Your task is to find the memory leak and develop a solution. When you find the solution you will edit leak_fix.py with the location of the leak and the line of c code needed to fix it. For example if there a file called example.c which had a memory leak that could be solved by freeing the variable weezy right before line 15, then you would fill the python file to contain.
filename = "example.c" linenum = 15 line = "free (weezy);"
We will insert the line you specified in the file you specified via a script. You only need to supply a working line number (not any particular line number). The line you insert should be a valid line of C code. This exercise is not meant to be difficult but is intended to get you to explore learning how to use testing software from documentation. It is of course possible to brute force but it will defeat the purpose and most likely take longer. Because of these goals we will have the following rules:
- You may not share any information about the file to check, the line number, or the variable that needs to be freed.
- You may not post any information about the proper way to use valgrind to find the memory leak. Half this task is about learning how to read documentation.
Debugging and Testing
Your code is compiled with the -g flag, so you can use CGDB to help debug your program. While adding in print statements can be helpful, CGDB can make debugging a lot quicker, especially for memory access-related issues. While you are working on the project, we encourage you to keep your code under version control via your github classroom account.
In addition, we have included a few functions to help make development and debugging easier:
- print_image(const unsigned char *data, int width, int height): This function takes in an array of pixels and prints their values in hex to standard output.
- save_image(char *filename, const unsigned char *data, int width, int height): This function takes in an array of pixels and saves them to a new bmp file at a specified filename.
- print_qtree(qNode *qtree_root): This function takes in a qNode and prints out the quadtree.
- print_compressed(qNode *qtree_root): This function takes in a qNode and prints out the compressed representation of the quadtree.
The test cases we provide you are not all the test cases we will test your code with. You are highly encouraged to write your own tests before you submit. Feel free to add additional tests into the skeleton code, but do not make any modifications to function signatures or struct declarations. This can lead to your code failing to compile during grading.
Running make check will run the test cases against your code. You will see results like this:
$ make check
Running: ./depth_map -l test/images/quilt1-left.bmp -r test/images/quilt1-right.bmp -h 0 -w 0 -t 1 -o test/output/quilt1-output.bmp -v
Wrong output. Check test/output/quilt1-output.txt and test/expected/quilt1-expected.txt
...
You can open up test/output/quilt1-output.bmp with an image viewer to see what kind of depth map your algorithm produced. You can open up test/output/quilt1-output.txt with a text editor to see the actual values it produced. The expected values will be in test/expected/quilt1-expected.txt.
CUnit
For further testing you can optionally write cunit tests, whose documentation can be found here. A starter framework has been provided showing sample tests on an example helper function square_euclidean_distance (). These CUnit tests are not graded and do not test much at all. Instead these are provided to give you a starting framework to run these tests. CUnit is already installed on the hive. You can run the CUnit tests with:
$ make run-unit-tests
The result of which is a breakdown for what tests you pass. For example initially it will look like:
Restoring Your Work
Before you turn in your project you should ensure that if you checkout the skeleton code and only swap in the files you are allowed to submit that the project will work as intended. You can use the git checkout command to do so, but be careful about the arguments you pass in as this will overwrite files. (Git will usually make sure you've committed changes before running the checkout though.)
$ git fetch starter $ git checkout starter/master [files]
Before you submit, make sure you test your code on the Hive machines. We will be grading your code there. IF YOUR PROGRAM FAILS TO COMPILE, YOU WILL AUTOMATICALLY GET A ZERO FOR THAT PORTION (ie. If depth_map works but quadtree doesn't compile, you will receive points for depth_map but none for quadtree). There is no excuse not to test your code.
Submission
Submitting is a two step process. You will need to submit on both the hive machine through glookup (where we will actually grade the submission) and tag your submission on github in case any issues arise. The full project 1-1 is due Tuesday 9/18 at 23:59.
To submit the full proj1-1 through glookup, enter in the following on the hive machine. You should be turning in calc_depth.c, make_qtree.c, and leak_fix.py.
$ cd ~/fa18-proj1-[YOUR USERNAME] $ submit proj1-1
To tag the commit of your submission on github run the following commands.
$ cd ~/fa18-proj1-[YOUR USERNAME] $ git add -u # should add all unmodified files in proj1 directory $ git commit -m "Project 1-1 submission" # or any other commit msg $ git tag -f "proj1-1-sub" # The tag MUST be "proj1-1-sub". Failure to do so will result in a loss of credit. $ git push origin master --tags # Note the --tags must be included to push tags to github
Part 2 (Due 10/1 @ 23:59:59)
NOTE: Do not write C code and compile it to RISC-V or refer to compiled code as a reference while completing this part of the project--this will be considered academic dishonesty. The intention of this assignment is for you to get practice writing code in RISC-V.
Objective
In the first part of the project we looked at a simple computer vision algorithm that generates displacement maps from stereo images. We also looked at compressing the displacement maps using a quadtree data structure. In this part you will solve two complementary tasks using the RISC-V instruction set.
For the first task, we will implement a pseudorandom number generator. Random number generators have a wide range of applications, but the connection to this project is that it can be used with a displacement map to generate random dot autostereograms. Random dot autostereograms (optional for this project) are random-looking images that, when viewed wall-eyed or cross-eyed, will give the illusion of a 3D image. With a little more work, between part 1 and part 2, the entire project will enable you to capture 3D data from the environment and then visualize it in a 3D autostereogram!
As a complement to the quadtree compression from part 1, for the second task, we will implement a decompression procedure that returns a displacement map from a quad-tree data structure.
Getting started
For this part, we'll continue to to use your existing project 1 repository and the same starter code repository. If everything was setup correctly from part 1, pull the updated starter code from the fa18-proj1-starter code repository to get started.
If you do not have the starter repository added as a remote, you will need to add it first.
$ git remote add starter https://github.com/61c-teach/fa18-proj1-starter.git
Then, fetch the files from the remote.
$ git fetch starter
Finally, create a new branch based on the remote's part-2 branch.
$ git checkout -b part-2 starter/part-2
Since we've created a new branch, when pushing changes to your private GitHub Classroom repository, make sure to push the part-2 branch instead of the master branch.
$ git push origin part-2
The files you will need to modify and submit are:
-
lfsr_random.s: Generates a random number using a LFSR. You will implement thelfsr_random()function. -
quad2matrix.s: Coverts a quadtree into the original image. You will implement thequad2matrix()function.
You are free to define and implement additional helper functions, but if you want them to be run when we grade your project, you must
include them in lfsr_random.s or quad2matrix.s. Changes made to any other files will be overwritten when we
grade the project.
The rest of the files are part of the framework. Familiarize yourself with the starter code before writing any code of your own.
combine.py: A Python 3 program which will link all of the programs together.matrix.s: The main program for quad2matrix, for linking.print_helpers.s: Some helper functions to print values.print_matrix.s: A helper function that prints a 2D matrix of arbitrary size.quad2matrix_data.s: A test case for quad2matrix.random.s: The main program for lfsr_random, for linking.
Task A (Due 10/1)
Your first task will be to implement the pseudorandom number generator. Edit the function in lfsr_random.s to implement the
16-bit LFSR from Lab 2.
Implement the 16-bit pseudorandom number generator from lab 2, but now in RISC-V. Your function must follow these specifications exactly. The solution in C has been made available for you. Note that this version performs the calculate-shift operation in a loop, 16 times in total. Your lab 2 code only performed one shift per function call, whereas this version will perform 16 shifts per function call. This is done in order to shift out all 16 old bits for 16 new bits.
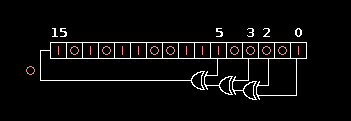
static uint16_t reg = 0x1;
for (int i = 0; i < 16; i++) {
uint16_t highest = ((reg >> 0) ^ (reg >> 2) ^ (reg >> 3) ^ (reg >> 5));
reg = (reg >> 1) | (highest << 15);
}
return reg;
There are no arguments for lfsr_random. You will use the .data section of lfsr_random.s to store your state.
Your return value should be a 16-bit number (the upper 16 bits of a0 should be 0).
Write your function in the file lfsr_random.s. Even if you've implemented your function correctly, if you paste this file directly into Venus, you will get an infinite loop. See the "Debugging and Testing" section for instructions on how to test your LFSR; we've provided a method for you to conveniently test your function.
Task B (Due 10/1)
Your second task will be to take the quadtree you built in Part 1 of the project and turn it back into the row-major 1-D array (which represents a 2-D image matrix). Recall that our quadtrees are structured like this:
struct quadtree {
int leaf;
int size;
int x;
int y;
int gray_value;
qNode *child_NW, *child_NE, *child_SE, *child_SW;
};
Your task is to implement the function in quad2matrix.s. It takes in a pointer to the root of a quadtree, a pointer to the first element of the matrix you will fill (already allocated for you), and the width of the matrix. Your function must traverse through the nodes of the tree and fill in the matrix with the correct values for each quadrant. See the "Debugging and Testing" section for instructions on how to test and debug your quad2matrix function.
Here are some tips:
- You are provided with the matrix you are writing your depth map into (in the default file, its dimensions are 8 x 8; note this size may change, so do not hard-code the value in your code) already, with all 0 values.
- Each element in the matrix is a byte (8 bits), not a word.
- You can assume that non-leaf nodes have a gray_value of -1, and that leaf nodes will have a gray value that is between 0 and 255, inclusive.
- You can assume that leaf nodes have NULL (0) in their children pointers.
- You can assume that int leaf; is either 1 (leaf) or 0 (non-leaf).
- You can assume that sizeof(int), sizeof(qNode*), and sizeof(void*) are 4 and that structs are tightly-packed.
- Make sure to test your code against other sparse matrices. You can generate your own sparse matrix by following the format in quad2matrix_data.s See "Debugging and Testing" for more details.
For a hint as to how to get started with designing the algorithm for this task, here are two high-level approaches we recomend trying.
- Go through the matrix pixel by pixel. Find the quadtree node corresponding to the pixel and then fill in that pixel's value.
- Explore the quadtree recursively, where the base case of reaching a leaf fills in all of the corresponding pixels in the matrix.
Debugging and Testing
A testing framework and one sample test for each function is provided for you. See each file's respective section below for more detailed instructions.
LFSR
To test your LFSR, run the following from your proj1-2 directory:
$ python combine.py random.s
If you have an error running this function, try running it with "py" or "python3". Running combine.py will put your lfsr_random function into a file called a.S. a.S calls your lfsr_random function 20 times and prints the result of each call followed by a newline. You can copy and paste the contents of a.S into Venus. If it is working correctly, this is what you will see as output in the console of the simulator:
26625 5185 27515 38801 56379 52819 14975 21116 38463 54726 38049 26552 4508 46916 37319 41728 23224 26004 11119 62850
Your LFSR should also work on other non-zero inputs. To test it, you can run the provided implementation of the LFSR in C twenty times, with values of reg other than 1, and change the .word labeled "lfsr" in the a.S file you produce to the same value (e.g. 0x5, 0x7, 0x972, etc.). The list of values that your lfsr_random function produces should be the same as the values that your C function produces. For example, if you replaced both values with 0x5 these are the 20 outputs that you should get:
40964 20741 44524 24133 28910 14671 59903 18928 22781 22298 21127 40674 18033 56592 18206 35842 27362 38481 44477 54792
Quadtree to Matrix
We have provided a print_matrix function that will be very useful to see the output matrix you are filling. The default data in quad2matrix_data.s is for an 8 x 8 depth map, structured the same way as the example quadtree we've used in the spec.
To test your quad2matrix function, run the following from your proj1-2 directory:
$ python combine.py matrix.s
This will produce an a.S file that will run your quad2matrix function on an example quadtree and print the resulting matrix. If you copy and paste the contents of a.S into Venus, the output should look like this:

Notice that what is printed is one 32 bit integer in hex per index of the matrix. The matrix is still a character array; the print_matrix function prints each 8 bit character index as a 32 bit hex number because otherwise, the null character '\0' would not print properly. Keep this in mind when interpreting your output and debugging. Essentially, you can ignore the top 6 hex digits of each matrix index, as they should always be 0.
You should also write your own quadtree tests. To do this, you will have to construct the expected quadtree input. After you come up with a depth map and the corresponding quadtree, there are two steps to turning them into a test. First, make a copy of your matrix.s file, and your quad2matrix_data.s file. You should name them something different, e.g. matrix_2.s and quad2matrix_data_2.s. In your quad2matrix_data_2.s file, specify your quadtree. The example included in the starter code is for a quadtree for a 8 x 8 depth map. This is the part of the code that corresponds to the quadtree:
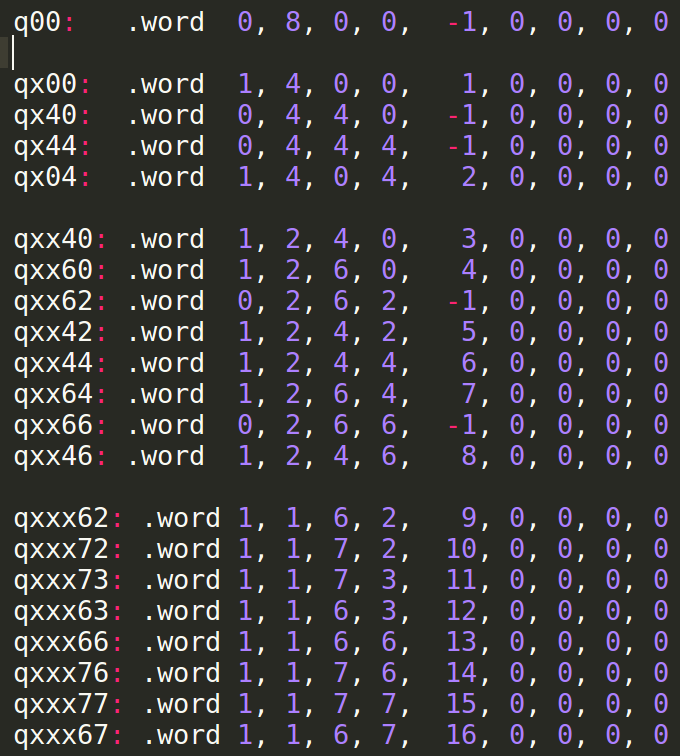
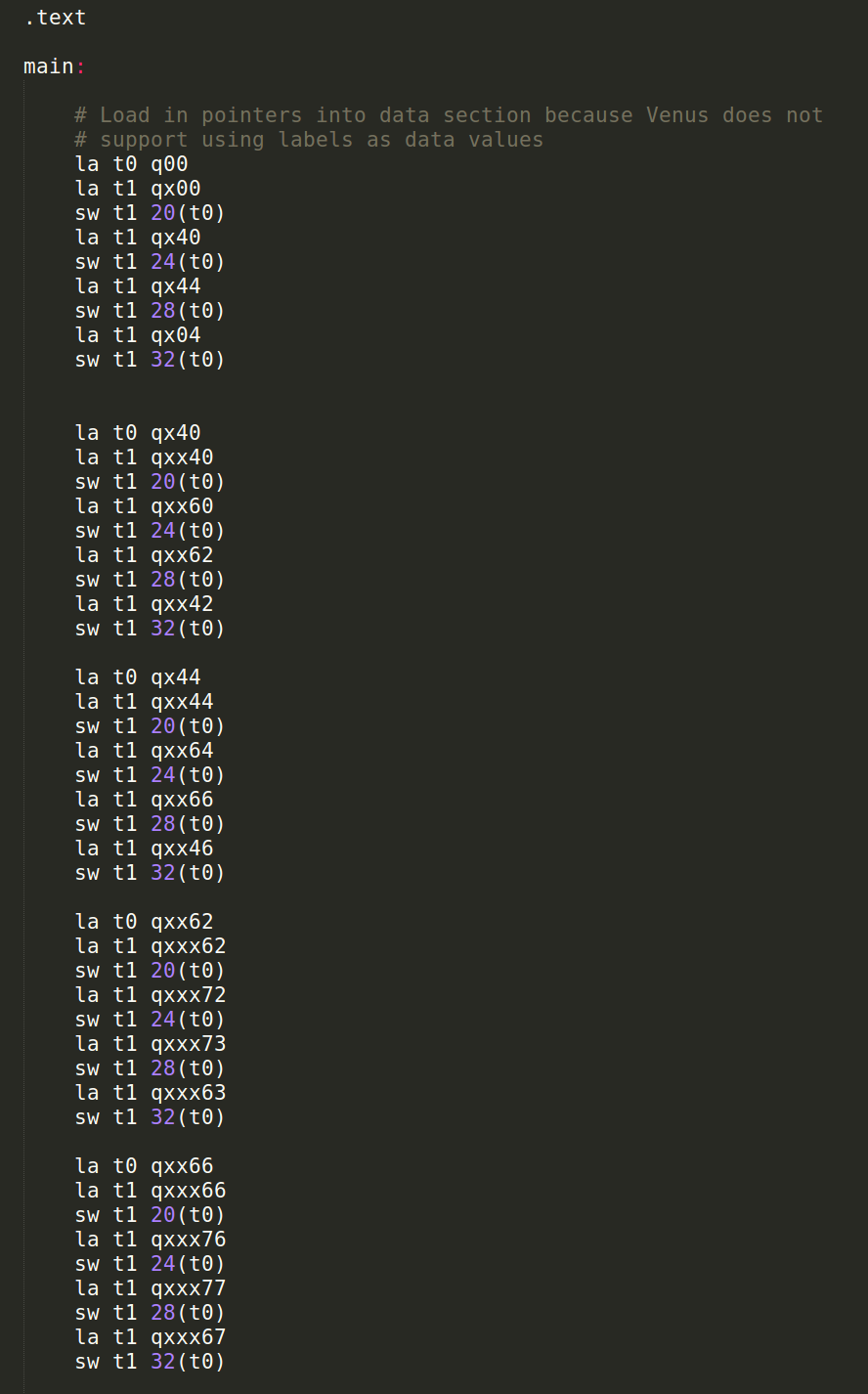
You should notice that the quadtree representation has 0's where all the pointers should go, meaning they are NULL pointers. This is because Venus does not allow you to load labels in the data section, so the appropriate pointers must be added to their respective quadtree nodes by hard-coding them into the beginning of your .text section in matrix_2.s. For the test we have provided to you, this is the portion where the quadtree nodes are given the correct labels for their respective children:
Finally, modify the bottom of matrix_2.s so that you are including your quad2matrix_data_2.s rather than quad2matrix_data.s. This is what the include section looks like:
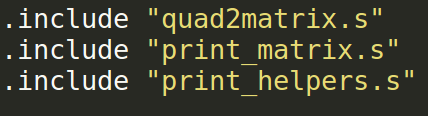
Now, you can produce the a.S file for your custom test with the following command:
$ python combine.py matrix_2.s
Submission
The full proj1-2 is due Monday, 10/1. To submit proj1-2, enter in the following. You should be turning in lfsr_random.s and quad2matrix.s.
$ submit proj1-2
Also be sure to push a commit with your final submission to Github, and tag it "proj1-2-sub" with the following steps:
$ cd fa18-proj1-[YOUR USERNAME] # Navigate into your project 1 repo, whatever it is called $ git add -u # Add all modified files $ git commit -m "Final submission for Proj 1-2" # Any commit message is OK here $ git tag -f "proj1-2-sub" # Tag this commit as the one you want to submit with "proj1-2-sub" exactly $ git push origin part-2 --tags # Since you created a branch, push to that branch