Part A: Math Functions
In this part, you will implement a few math operations that will be used for classification later.
Task 1: Absolute Value (Walkthrough)
To familiarize you with the workflow of this project, we will walk you through this task. This section is available in both video and written form.
To follow along with the videos, watch the videos in this playlist.
Running Tests
In this project, tests are written in Python and compiled into RISC-V assembly.
To see the Python source for the tests, navigate to the unittests directory where the tests are located. Inside the unittests directory, unittests.py is where we've provided tests for your functions.
Take a look at the contents of unittests.py. Although the tests are written for you in Tasks 1-4, it helps to be familiar with the unit testing framework to understand what the tests are doing.
To run the tests, start by running make help in the unittests directory on your local machine. This gives you an overview of the commands you can run for testing. In particular, make test-partA compiles and runs all the tests for Part A. You can also provide the name of a specific function to compile and run all the tests for that particular function. For this task, since we are implementing the abs function, you can run make test-abs on your local machine.
Since we haven't implemented the abs function yet, all of the tests are failing.
Using VDB to debug tests via Venus
First, open up Venus in your web browser and mount your files. (Refer back to the setup section of the spec if you're having trouble.)
You can edit files in a text editor or directly in Venus. To edit files in Venus, switch to the Files tab. Here you can open and edit assembly files. Remember to save your files frequently with control+S (Windows) or command+S (Mac). Venus does not auto-save as you work.
Open src/abs.s. This is the function we need to implement in this task. At the moment, the function just returns 0.
To see why the abs function is failing right now, we can set a breakpoint. Type ebreak at Line 13. This places a breakpoint just before the mv a0, zero instruction.
To start the debugger, go to Venus and navigate to unittests/assembly/TestAbs_test_one.s. Note that the assembly folder will only be made after you run the make command to generate the assembly test files.
Click on VDB to start the debugger. When we click Run, the debugger will pause at the breakpoint we set. While paused, you can inspect the registers and memory. In particular, notice that register a0 contains the argument 1 here, because this test inputs the argument 1.
You can also step through code line-by-line in the debugger. Click Step to execute the next instruction, mv a0, zero. This causes the register a0 to take the value 0.
Now we can implement the abs function by putting this in src/abs.s:
abs:
# Return if non-negative
bge a0, zero, done
# Negate a0 if negative
sub a0, x0, a0
done:
ret
Try running make test-abs again, and now you should see that all the tests pass.
Task 2: ReLU
Conceptual Overview: Arrays
In this project, we will be working with integer arrays. Recall that the integers in an integer array are stored in a consecutive block of memory.
To pass an integer array as an argument, we will pass a pointer to the start of the integer array, and the number of elements in the array.
In this diagram, register a0 stores the first argument (the address of the start of the array). Register a1 stores the second argument (the number of integers in the array).
Conceptual Overview: ReLU
The ReLU function takes in an integer array and sets every negative value in the array to 0. Positive values in the array are unchanged. In other words, for each element x in the array, ReLU computes max(x, 0).
ReLU should modify the array in place. For example, if the above integer array is passed into ReLU, the result would be stored in the same place in memory:
Note that the negative values in the array were set to 0 in memory.
Your Task
Fill in the relu function in src/relu.s.
relu: Task 2. |
|||
| Arguments | a0 |
int * |
A pointer to the start of the integer array. |
a1 |
int |
The number of integers in the array. You can assume that this argument matches the actual length of the integer array. | |
| Return values | None | ||
If the input is malformed in the following ways, put the appropriate return code into a1 and run call exit2 to quit the program. (For example, if the length of the array is less than 1, run li a1 57 and call exit2.)
| Return code | Exception |
| 57 | The length of the array is less than 1. |
To test your function, run make test-relu. Refer back to Task 1 for debugging instructions.
Task 3: Argmax
Conceptual Overview: Argmax
The argmax function takes in an integer array and returns the index of the largest element in the array. If multiple elements are tied as the largest element, return the smallest index.
For example, if the integer array [-6, -1, 6, 1] is passed into the argmax function, the output should be 2, because the largest integer (6) is located at index 2 in the array. If the integer array were instead [6, 1, 6, 1], then the output should be 0, because the largest integer (6) is first found at index 0.
Your Task
Fill in the argmax function in src/argmax.s.
argmax: Task 3. |
|||
| Arguments | a0 |
int * |
A pointer to the start of the integer array. |
a1 |
int |
The number of integers in the array. You can assume that this argument matches the actual length of the integer array. | |
| Return values | a0 |
int |
The index of the largest element. If the largest element appears multiple times, return the smallest index. |
If the input is malformed in the following ways, put the appropriate return code into a1 and run call exit2 to quit the program.
| Return code | Exception |
| 57 | The length of the array is less than 1. |
To test your function, run make test-argmax. Refer back to Task 1 for debugging instructions.
Task 4: Dot Product
Conceptual Overview: Dot Product
The dot product function takes in two integer arrays, multiplies the corresponding entries of the arrays together, and returns the sum of all the products.
For example, if these two integer arrays were passed into the dot product function, the function would return (1*6) + (2*1) + (3*6) + (4*1) + (5*6) + (6*1) + (7*6) + (8*1) + (9*6) = 170.
Conceptual Overview: Array Strides
Instead of iterating through every element of the array, what if we want to iterate through every other element, or every third element? To do this, we will define the stride of an array.
To iterate through an array with stride n, start at the beginning of the array and only consider every nth element, skipping the elements in between.
Note that the stride is given in number of elements, not number of bytes. This means that iterating with stride 1 is equivalent to iterating through every element of the array.
For example, in the above diagram, both arrays are using stride 2, so we skip every other element in the array. 5 elements should be considered, so we stop after multiplying 5 pairs of elements together. The function would return (1*6) + (3*6) + (5*6) + (7*6) + (9*6) = 150.
In the above diagram, the first array is using stride 2, so we skip every other element in this array. The second array is using stride 3, so we use every third element in this array. 3 elements should be considered, so we stop after multiplying 3 pairs of elements together. The function would return (1*6) + (3*1) + (5*6) = 39.
Your Task
Fill in the dot function in src/dot.s.
dot: Task 4. |
|||
| Arguments | a0 |
int * |
A pointer to the start of the first array. |
a1 |
int * |
A pointer to the start of the second array. | |
a2 |
int |
The number of elements to use in the calculation. | |
a3 |
int |
The stride of the first array. | |
a4 |
int |
The stride of the second array. | |
| Return values | a0 |
int |
The dot product of the two arrays, using the given number of elements and the given strides. |
If the input is malformed in the following ways, put the appropriate return code into a1 and run call exit2 to quit the program.
| Return code | Exception |
| 57 | The length of either array is less than 1. |
| 58 | The stride of either array is less than 1. |
To test your function, run make test-dot. Refer back to Task 1 for debugging instructions.
Task 5: Matrix Multiplication
Conceptual Overview: Storing Matrices
A matrix is a 2-dimensional array of integers. In this project, matrices will be stored as an integer array in row-major order. Row-major order means we each row of the matrix consecutively in memory as a 1-dimensional integer array.
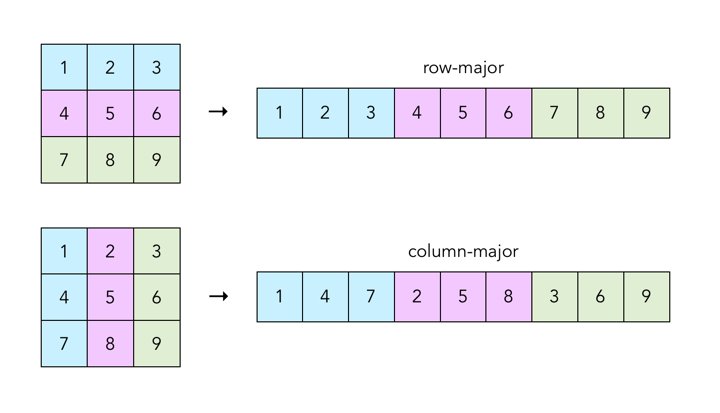
Conceptual Overview: Matrix Multiplication
The matrix multiplication function takes in two integer matrices A (dimension n × m) and B (dimension m × k) and outputs an integer matrix C (dimension n × k).
To calculate the entry at row i, column j of C, take the dot product of the ith row of A and the jth column of B. Note that this can be done by calling the dot function with the proper strides.
For example, in the above diagram, we are computing the entry in row 1, column 1 of C by taking the dot product of the 1st row of A and the 1st row of B.
In the above diagram, we are computing the entry in row 2, column 2 of C. Note that we are changing the pointer to the start of the array in order to access later rows and columns.
Your Task
Fill in the matmul function in src/matmul.s.
matmul: Task 5. |
|||
| Arguments | a0 |
int * |
A pointer to the start of the first matrix A (stored as an integer array in row-major order). |
a1 |
int |
The number of rows (height) of the first matrix A. | |
a2 |
int |
The number of columns (width) of the first matrix A. | |
a3 |
int * |
A pointer to the start of the second matrix B (stored as an integer array in row-major order). | |
a4 |
int |
The number of rows (height) of the second matrix B. | |
a5 |
int |
The number of columns (width) of the second matrix B. | |
a6 |
int * |
A pointer to the start of an integer array where the result C should be stored. You can assume this memory has been allocated (but is uninitialized) and has enough space to store C. | |
| Return values | None | ||
If the input is malformed in the following ways, put the appropriate return code into a1 and run call exit2 to quit the program.
| Return code | Exception |
| 59 | The height or width of either matrix is less than 1. |
| 59 | The number of columns (width) of the first matrix A is not equal to the number of rows (height) of the second matrix B. |
To test your function, run make test-matmul. Refer back to Task 1 for debugging instructions.
Task 6: Testing
In this task, you will be writing tests for some mathematical functions that have already been implemented for you.
Conceptual Overview: Loss Functions
A loss function takes in two integer arrays and outputs an integer array containing some measure of how different each pair of corresponding entries are. Some loss functions also output the sum of all the difference measurements. This project uses three different loss functions.
The absolute loss function computes and outputs the absolute difference between each pair of corresponding entries, and then outputs the sum of all the absolute differences.
The squared loss function computes and outputs the square of the difference between each pair of corresponding entries, and then outputs the sum of all the squared differences.
The zero-one loss function computes whether each pair of corresponding entries is equal, and does not output any sum.
These loss functions use a helper function initialize-zero. It takes in the length of the array as input and outputs a newly-allocated array of the given length, filled with zeros.
Your Task
Fill in the tests for the three loss functions and the initialize-zero helper function in unittests/studenttests.py.
We recommend looking through unittests/unittests.py to understand how the Python framework for writing tests works.
| Arguments | a0 |
int * |
A pointer to the start of the first input array. |
a1 |
int * |
A pointer to the start of the second input array. | |
a2 |
int |
The number of integers in the array. | |
a3 |
int * |
A pointer to the start of the output array, where the results will be stored. | |
| Return values | a0 |
int |
The sum of the elements in the output array. |
Submission and Grading
Submit your code to the Project 2A assignment on Gradescope.
To ensure the autograder runs correctly, do not add any .import statements to the starter code. Also, make sure there are no ecall instructions in your code.