Lab 7: Caches

Deadline: Friday, October 28, 11:59:59 PM PT

Setup

In your labs directory, pull the files for this lab with:

git pull starter main

For this lab, record your answers to the Tasks questions in the Lab 7 Google Form.

• The Google Form is very simple and thus incapable of recognizing typos or incorrectly formatted answers. However, it features response validation and the ability to view your score. Please use these to verify your submission.
• You also have the ability to edit your response so you can submit the form to save your progress
• We suggest you have a single tab with this form open alongside the spec as you work on Lab 7.

---

Review: Cache Lines

Let's review how cache lines work. When we bring data from the main memory into the cache, it is done in the granularity of a cache line (or cache block). Typically cache lines are 64 bytes. This helps us take advantage of spatial locality.

Let's look at an example. The following shows a portion of main memory. The cache (not shown) has a line size of 64 bytes. If we want to access byte 199₁₀ and its not in the cache, we would bring bytes 192₁₀-255₁₀ into the cache

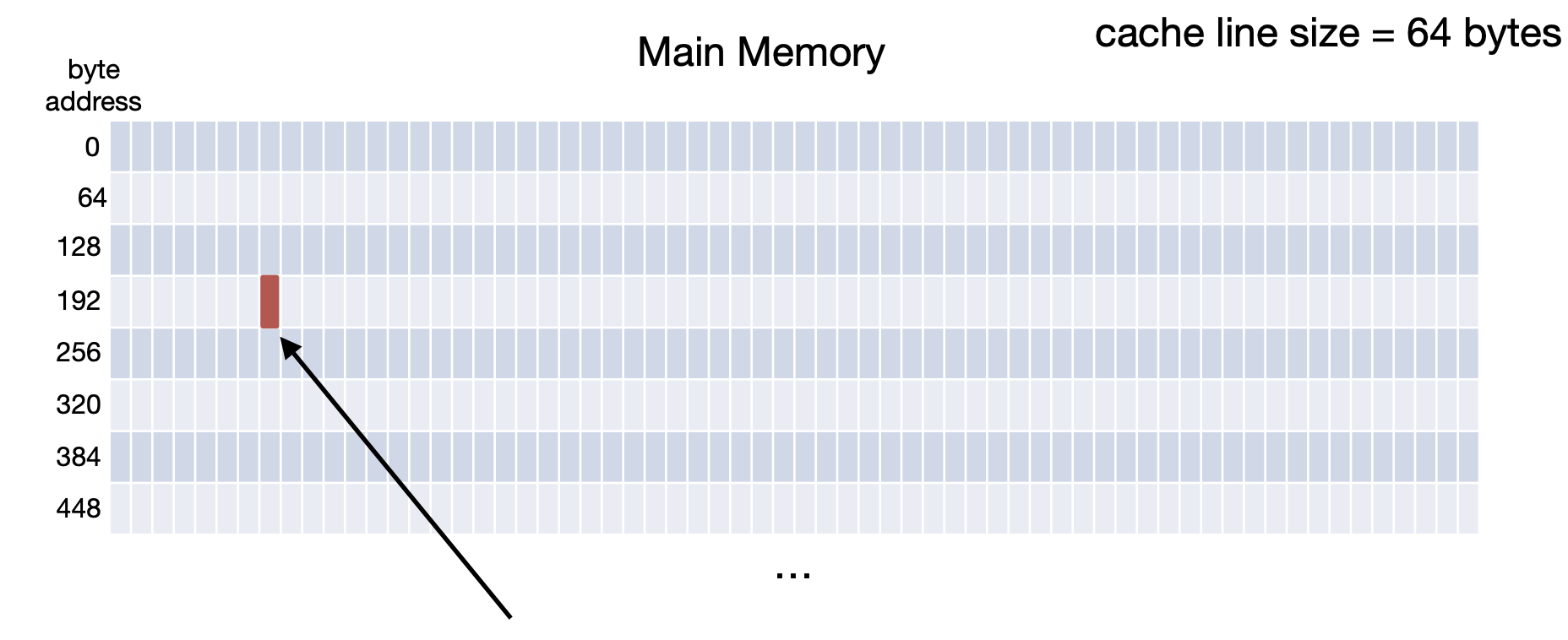
If we then wanted to access byte 255₁₀, we would get a cache hit because we just brought in the line that its in.

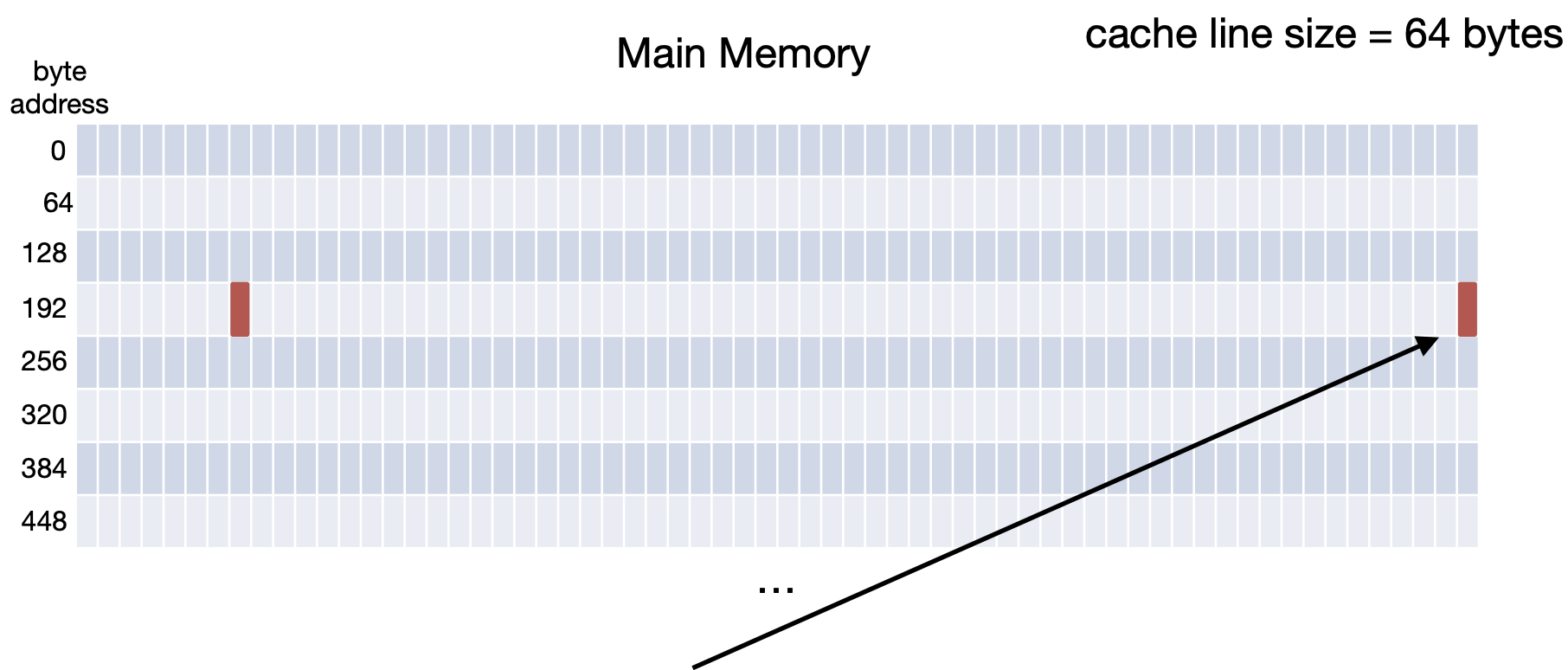
Finally, if we wanted to access byte 194₁₀, we would get a cache hit because we just brought in the line that its in.

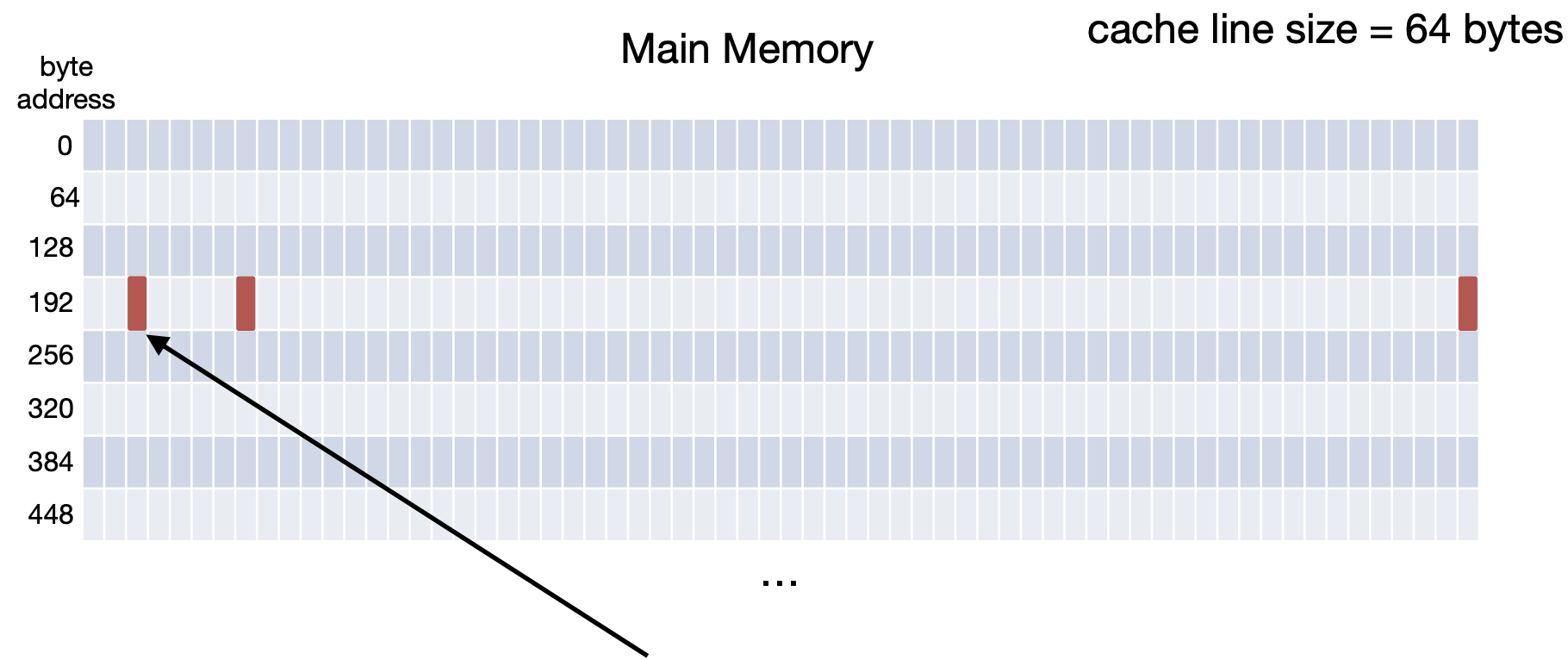
Exercise 1 - Cache Practice Problems

This exercise will analyze the performance of the following code under different cache and program configurations.

/* Assume that each value in array is initalized to 5
Declaration and initialization of `array` omitted */

void accessWords(int array_size, int step_size, int rep_count, int option) {
    for (int k = 0; k < rep_count; k++) { 
        for (int index = 0; index < array_size; index += step_size) {
            if (option == 0) {
                // Option 0: One cache access - write
                array[index] = 0; 
            } else {
                // Option 1: Two cache accesses - read AND write
                array[index] = array[index] + 1; 
            }
        }
    }
}

int main() {
    int array_size = 32;
    int step_size = 8;
    int rep_count = 4;
    int option = 0;
    accessWords(array_size, step_size, rep_count, option);
    return 0;
}

Scenario 1

Program Parameters:

• Array Size: 32 ints
• Step Size: 8
• Rep Count: 4
• Option: 0

Cache Parameters:

• Cache Levels: 1
• Block Size: 8 bytes
• Number of Blocks: 4
• Associativity: 1 (Direct Mapped)
• Block Replacement Policy: LRU

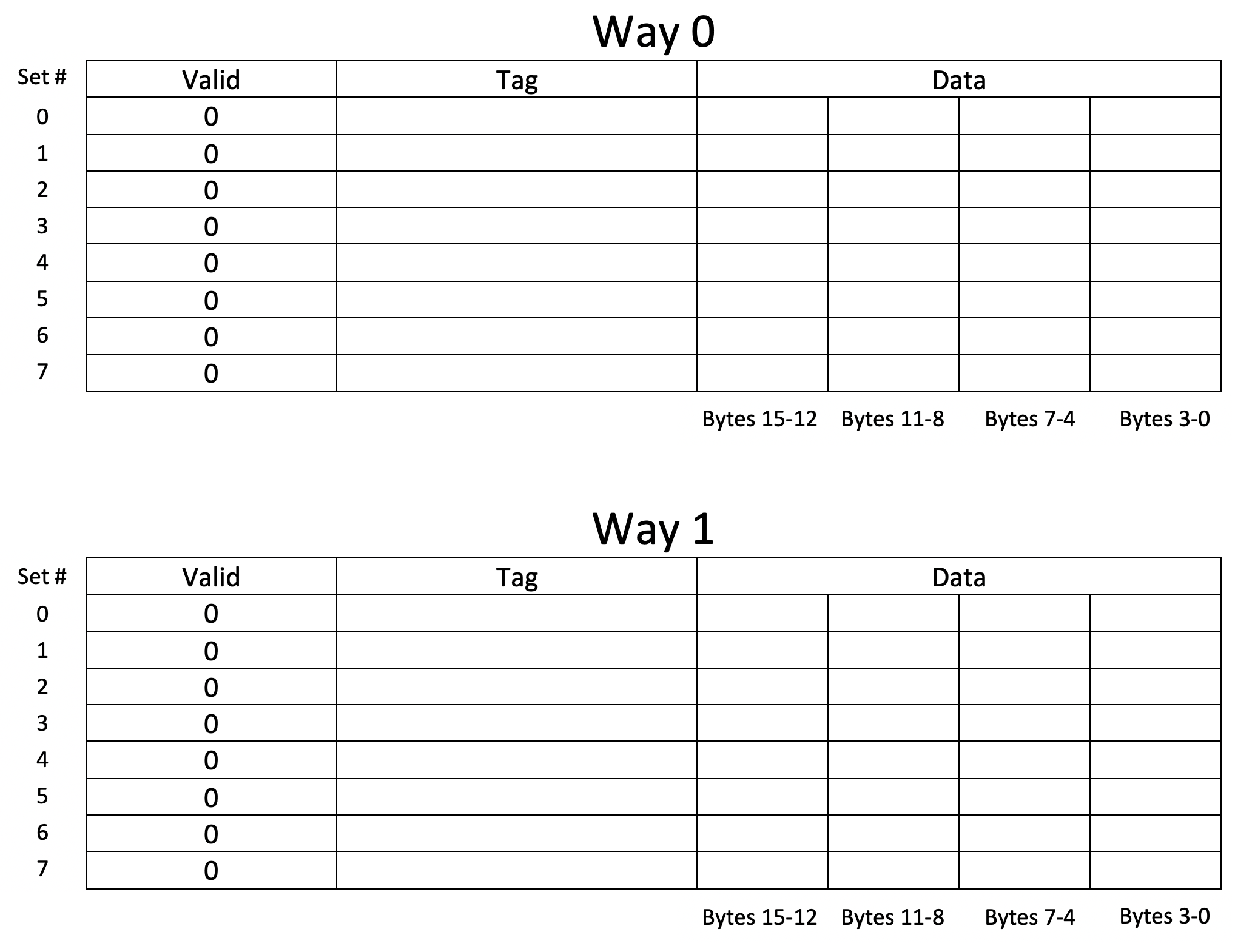
The layout of the cache can be seen here:

We'll walk through this scenario together.

Compute the Byte Addresses

First, we need to determine which elements in the array we are accessing. The array has 32 elements and the step size is 8, so we will access elements 0, 8, 16, and 24.

We will use the byte address of each element to determine where to place it in the cache. To determine the byte address, we will first find the byte offset of each element from the start of the array. Each element in the array takes up 4 bytes. The byte offset of each element is as follows:

Element 0 = 0 * 4 = 0

Element 8 = 8 * 4 = 32

Element 16 = 16 * 4 = 64

Element 24 = 24 * 4 = 96

If that doesn't make sense, consider the following 5-element array. The bytes that each element takes up are shown below. The 32-element array follows the same pattern.

To get the full byte address of each element, we need the address of the array. To make things simple, let's set the address of the array to be 0. This makes the byte address of each element equivalent to the byte offsets from the start of the array.

Compute TIO Bits

Next, we need to determine which bits of the address correspond to the tag, index, and offset. The number of tag, index, and offset bits given the above configuration are as follows:

#offset bits = log2(block size) = log2(8) = 3

#index bits = log2(num indicies) = log2(4) = 2

#tag bits = # address bits - # index bits - # offset bits = 32 - 3 - 2 = 27

Access Element 0

Byte Address: 0b 0000 0000 0000 0000 0000 0000 0000 0000

Tag	Index	Offset
0b 0000 0000 0000 0000 0000 0000 000	0b00	0b000

Fill in what the cache looks like after element 0 is accessed.

Here, we experience a compulsory cache miss because the element has never been in the cache. The cache line size is 8 and the size of each element is 4, so we end up brining in two elements into the cache. Remember that we initially set each element to be 5.

Access Element 8

Byte Address: 32 = 0b 0000 0000 0000 0000 0000 0000 0010 0000

Tag	Index	Offset
0b 0000 0000 0000 0000 0000 0000 001	0b00	0b000

Fill in what the cache looks like after element 8 is accessed.

Compulsory cache miss

Access Element 16

Byte Address: 64 = 0b 0000 0000 0000 0000 0000 0000 0100 0000

Tag	Index	Offset
0b 0000 0000 0000 0000 0000 0000 010	0b00	0b000

Fill in what the cache looks like after element 16 is accessed.

Compulsory cache miss

Access Element 24

Byte Address: 96 = 0b 0000 0000 0000 0000 0000 0000 0110 0000

Tag	Index	Offset
0b 0000 0000 0000 0000 0000 0000 011	0b00	0b000

Fill in what the cache looks like after element 24 is accessed.

Compulsory cache miss

We have just completed one iteration of the outer loop. The remaining iterations of the outer loop won't change the output of the program, but they can potentially change the hit rate of the cache.

The hit rate of the cache after the program finishes running is 0%.

Every access mapped to the same cache line. Each time we placed an item in the cache, we kicked out the item that was previously there. The first time that we accessed each element, we had a compulsory miss. The second, third, and forth time that we accessed each element, we had a conflict miss because the element was previously in the cache, but it was kicked out by another element.

In general, you can use the following steps to determine the type of miss

1. First, consider an infinite-size, fully-associative cache. every miss that occurs now is a compulsory miss.
2. Next, consider a finite-sized cache (of the size you want to examine) with full-associativity. Every miss now that is not in #1 is a capacity miss.
3. Finally, consider a finite-size cache with finite-associativity. All of the remaining misses that are not #1 or #2 are conflict misses.

Action Item

Make sure to fill out the questions in the answer form!

Scenario 2

Program Parameters:

• Array Size: 64 ints
• Step Size: 2
• Rep Count: 1
• Option: 1

Cache Parameters:

• Cache Levels: 1
• Block Size: 16 bytes
• Number of Blocks: 16
• Associativity: 2
• Block Replacement Policy: LRU

Action Item

Answer the questions found in the google form linked above.

Scenario 3

Program Parameters:

• Array Size: 32 ints
• Step Size: 1
• Rep Count: 1
• Option: 0

Cache Parameters:

• Cache Levels: 2

L1 Cache

• Block Size: 8
• Number of Blocks: 8
• Placement Policy:
• Associativity: 1 (Direct Mapped)

L2 Cache

• Block Size: 8
• Number of Blocks: 16
• Associativity: 1 (Direct Mapped)
• Block Replacement Policy: LRU

It's your turn to draw the caches on your own!

Action Item

Answer the questions found in the google form.

---

Exercise 2 - Loop Ordering and Matrix Multiplication

NOTE: For this exercise, using the hive machines is recommended! This exercise depends on certain performance characteristics that may be different on your local machine.

Matrices are 2-dimensional data structures where each data element is accessed via two indices. To multiply two matrices, we can simply use 3 nested loops below, assuming that matrices A, B, and C are all n-by-n and stored in one-dimensional column-major arrays:

for (int i = 0; i < n; i++)
    for (int j = 0; j < n; j++)
        for (int k = 0; k < n; k++)
            C[i+j*n] += A[i+k*n] * B[k+j*n];

Matrix multiplication operations are at the heart of many linear algebra algorithms, and efficient matrix multiplication is critical for many applications within the applied sciences.

In the above code, note that the loops are ordered i, j, k. If we examine the innermost loop (the one that increments k), we see that it...

• moves through B with stride 1 (j and n remain constant and we are adding k to this constant)
• moves through A with stride n (i and n remain constant and we multiplying k by n)
• moves through C with stride 0 (i, j, and n remain constant and k is not used)

To compute the nxn matrix multiplication correctly, the loop order doesn't matter.

BUT, the order in which we choose to access the elements of the matrices can have a large impact on performance. Caches perform better (more cache hits, fewer cache misses) when memory accesses take advantage of spatial and temporal locality, utilizing blocks already contained within our cache. Optimizing a program's memory access patterns is essential to obtaining good performance.

Take a glance at matrixMultiply.c. You'll notice that the file contains multiple implementations of matrix multiply with 3 nested loops.

Note that the compilation command in the Makefile uses the -O3 flag. It is important here that we use the -O3 flag to turn on compiler optimizations. Compile and run the code with the following command, and then answer the questions below:

make ex2

This will run some matrix multiplications according to the six different implementations in the file, and it will tell you the speed at which each implementation executed the operation. The unit "Gflops/s" means "Giga-floating-point-operations per second." THE BIGGER THE NUMBER THE FASTER IT IS RUNNING!

Action Item

To understand why certain orderings perform better than others, we need to look at the step size across each matrix in the inner loop. Smaller step sizes are going to exhibit better spatial locality.

Determine the step sizes of the following configurations. We gave you the first two to get you started.

ijk

Step size across A: n

Step size across B: 1

Step size across C: 0

ikj

Step size across A: 0

Step size across B: n

Step size across C: n

jik

Step size across A:

Step size across B:

Step size across C:

jki

Step size across A:

Step size across B:

Step size across C:

kij

Step size across A:

Step size across B:

Step size across C:

kji

Step size across A:

Step size across B:

Step size across C:

Your answers to the following questions should go into the corresponding section of the Lab 7 Google Form; all answers should be lowercased.

1. Which 2 orderings perform best for these 1000-by-1000 matrices?
2. Which 2 orderings perform the worst?

---

Exercise 3 - Cache Blocking and Matrix Transposition

NOTE: For this exercise, using the hive machines is recommended! This exercise depends on certain performance characteristics that may be different on your local machine.

Matrix Transposition

The swapping of the rows and columns of a matrix is called a "transposition". An efficient implementation can be quite helpful while performing more complicated linear algebra operations. The transpose of matrix A is often denoted as A^T. The naive implementation of transposing a matrix would look like the following:

void transpose_naive(int n, int blocksize, int *dst, int *src) {
    for (int x = 0; x < n; x++) {
        for (int y = 0; y < n; y++) {
            dst[y + x * n] = src[x + y * n];
        }
    }
}

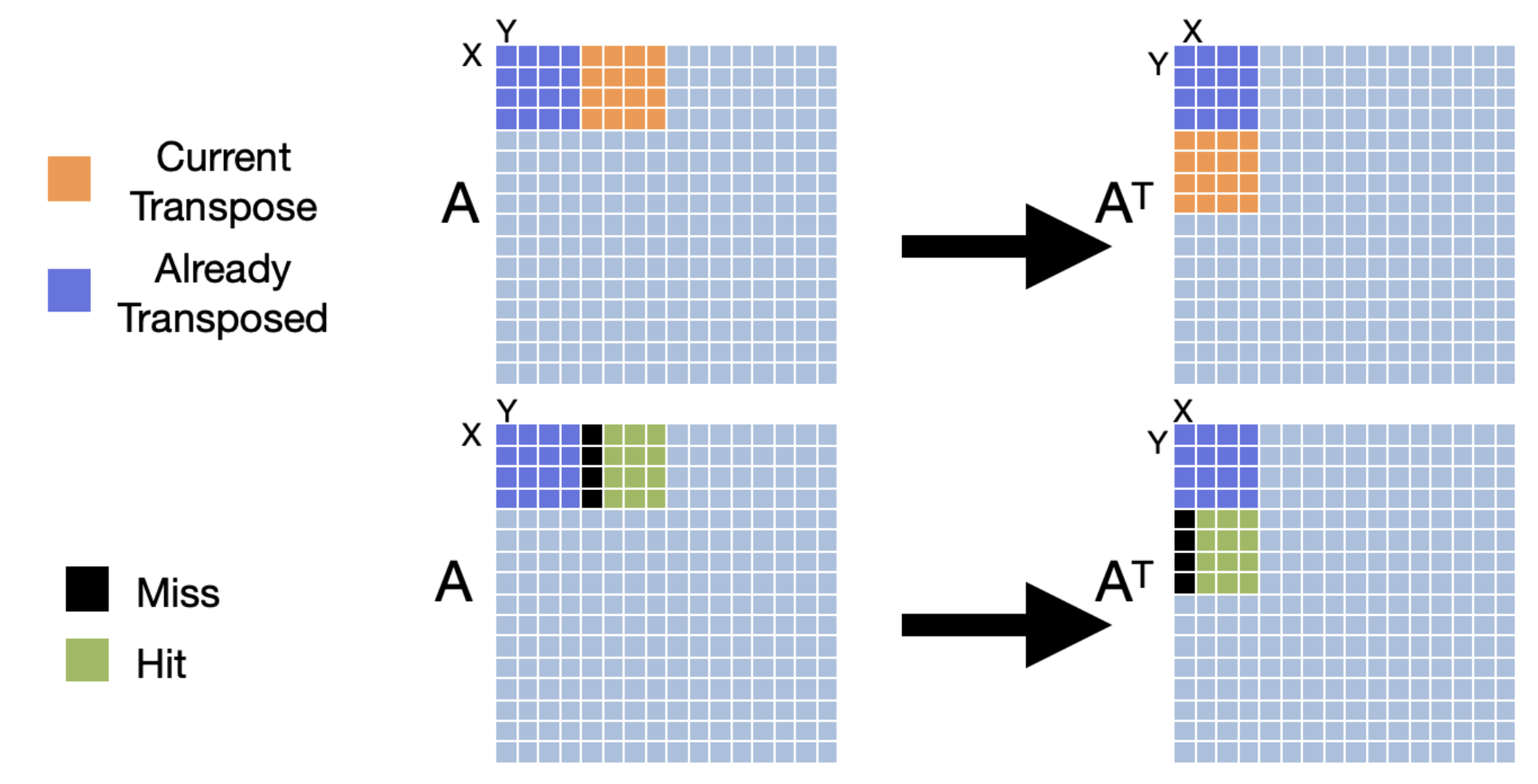
In this implementation, we access an entire row of src and an entire column of dst in one iteration of the inner loop. A visual representation of the first three iterations of the loop is given below.

---

---

---

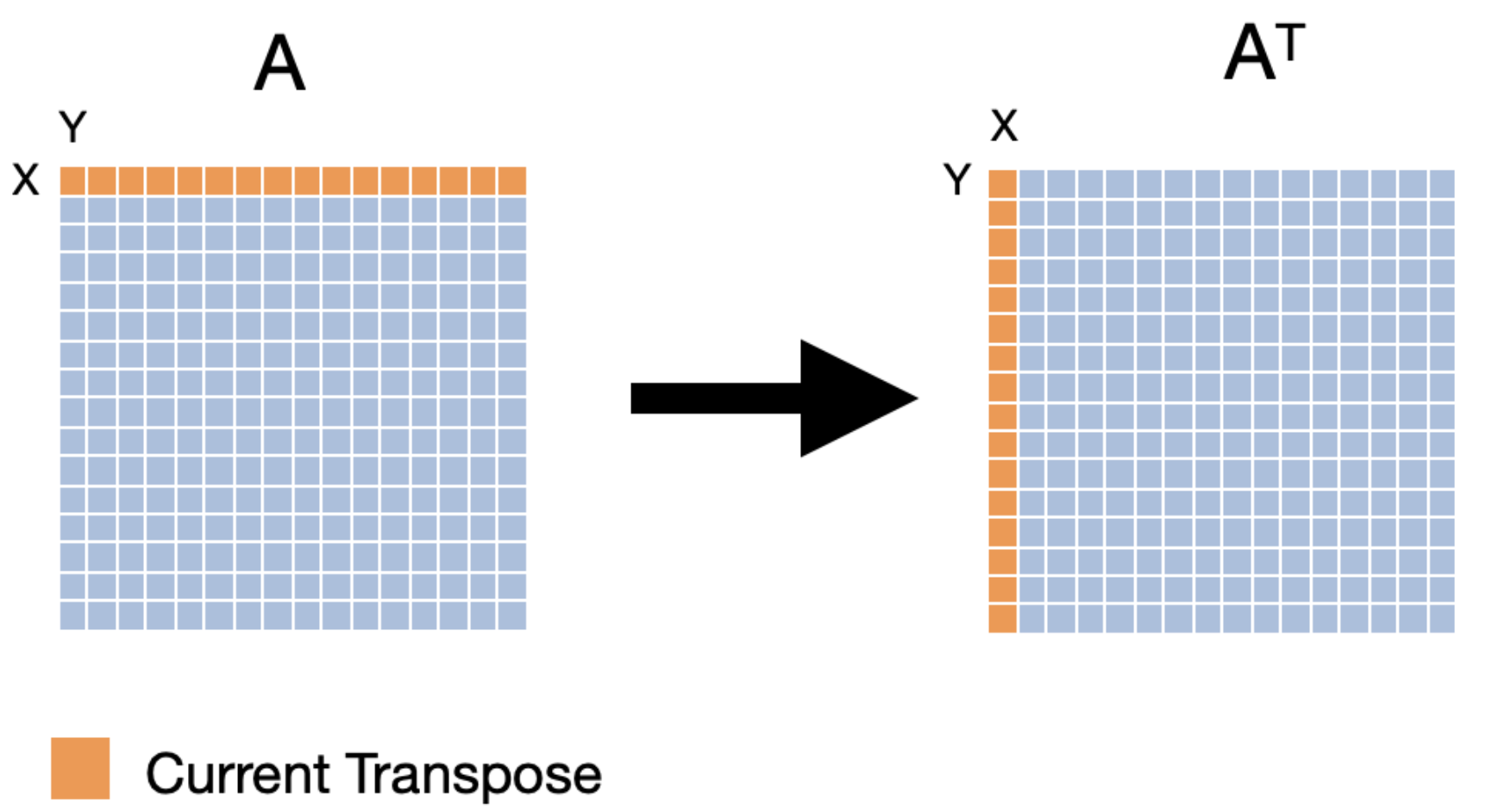
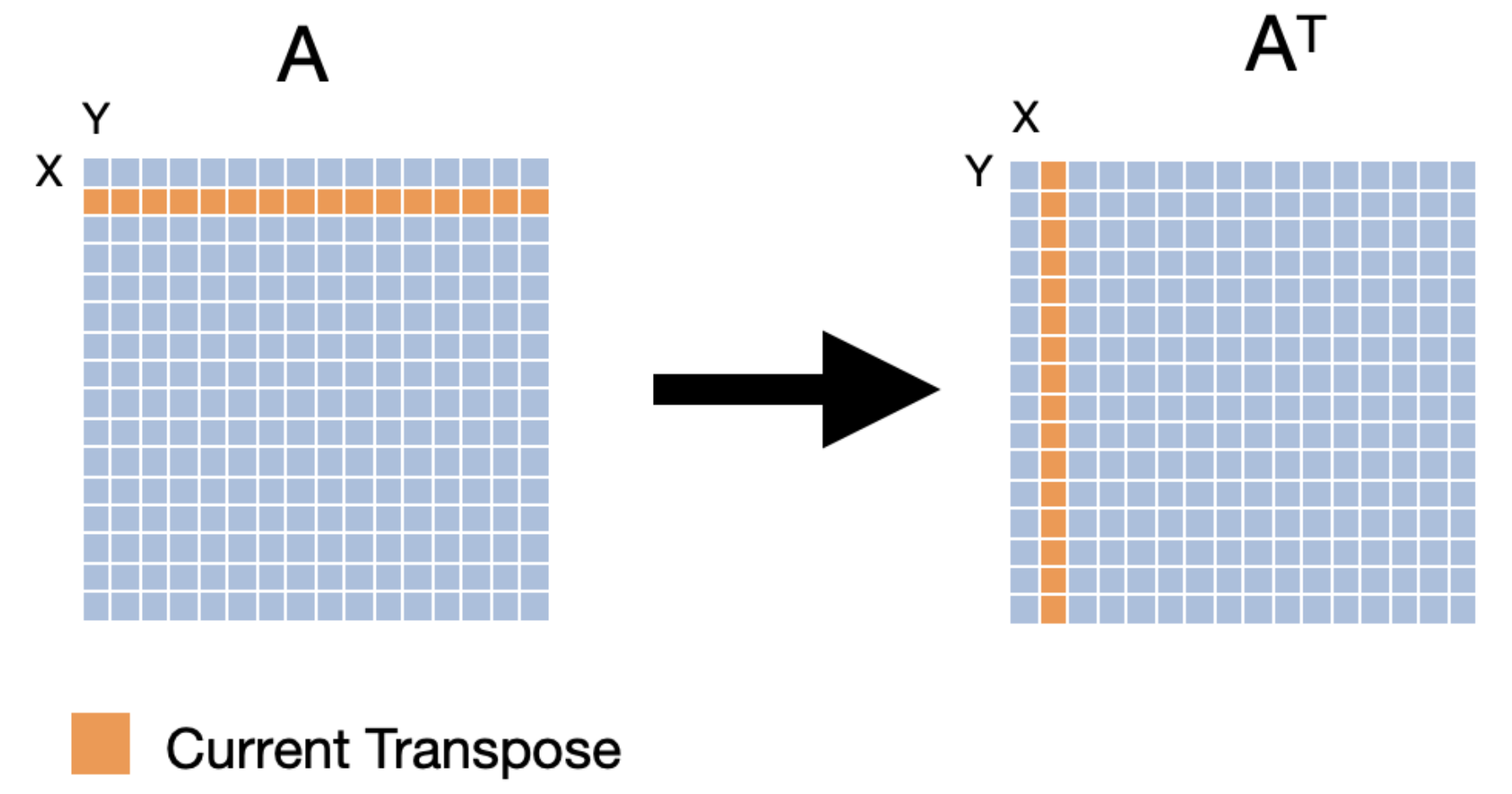
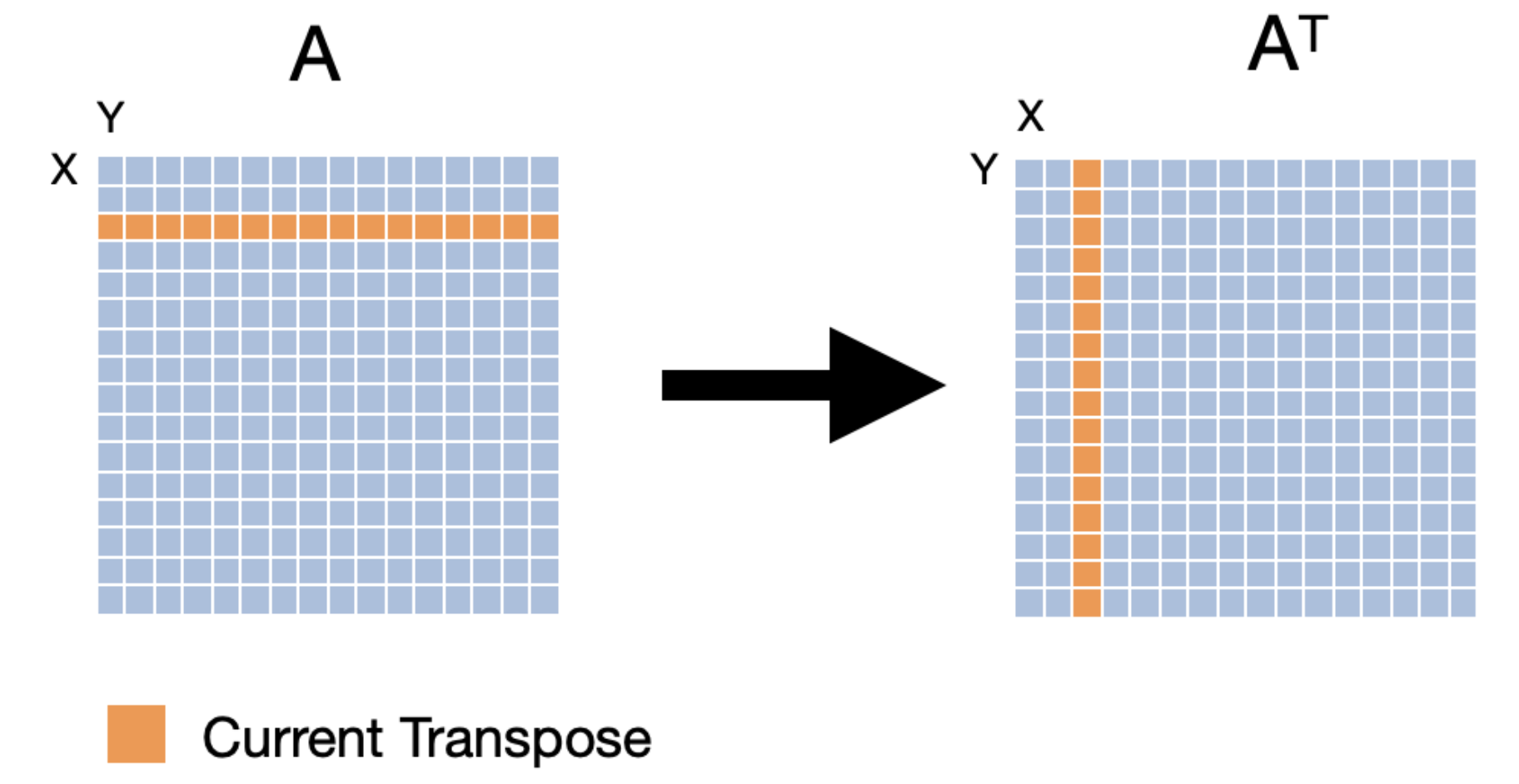
Let's think about what the cache access pattern would be for the implementation. Let's say that we have a fully associative cache with 16 lines and a line size of 16 bytes. If the elements in the cache are 4 bytes, the hit/miss pattern of the cache during the first iteration of the inner loop would look like the following.

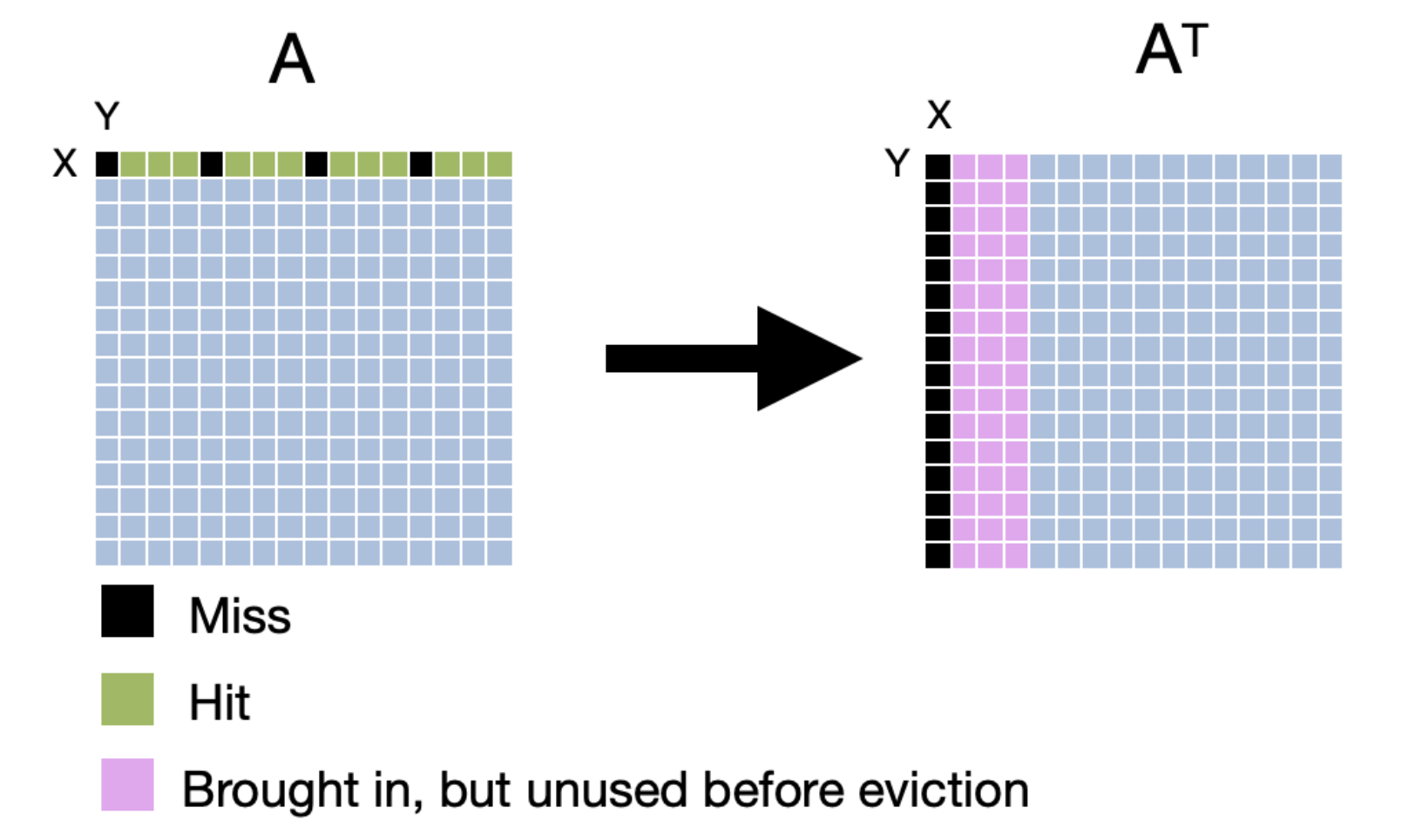
The hit rate when accessing the source matrix is 75% which is as good as it can be with the given cache configuration. The hit rate when accessing the destination matrix is 0. Let's see if we can improve this.

Cache Blocking

To improve the performance of our cache, we can use a technique called cache blocking. Cache blocking is a technique that attempts to reduce the cache miss rate by improving the temporal and/or spatial locality of memory accesses. To achieve this, we will transpose the matrix one "block" at a time. We will make sure that the number of bytes within the width of the block can fit into an entire cache line. The following images show three iterations of transposing the matrix one block at a time.

---

---

---

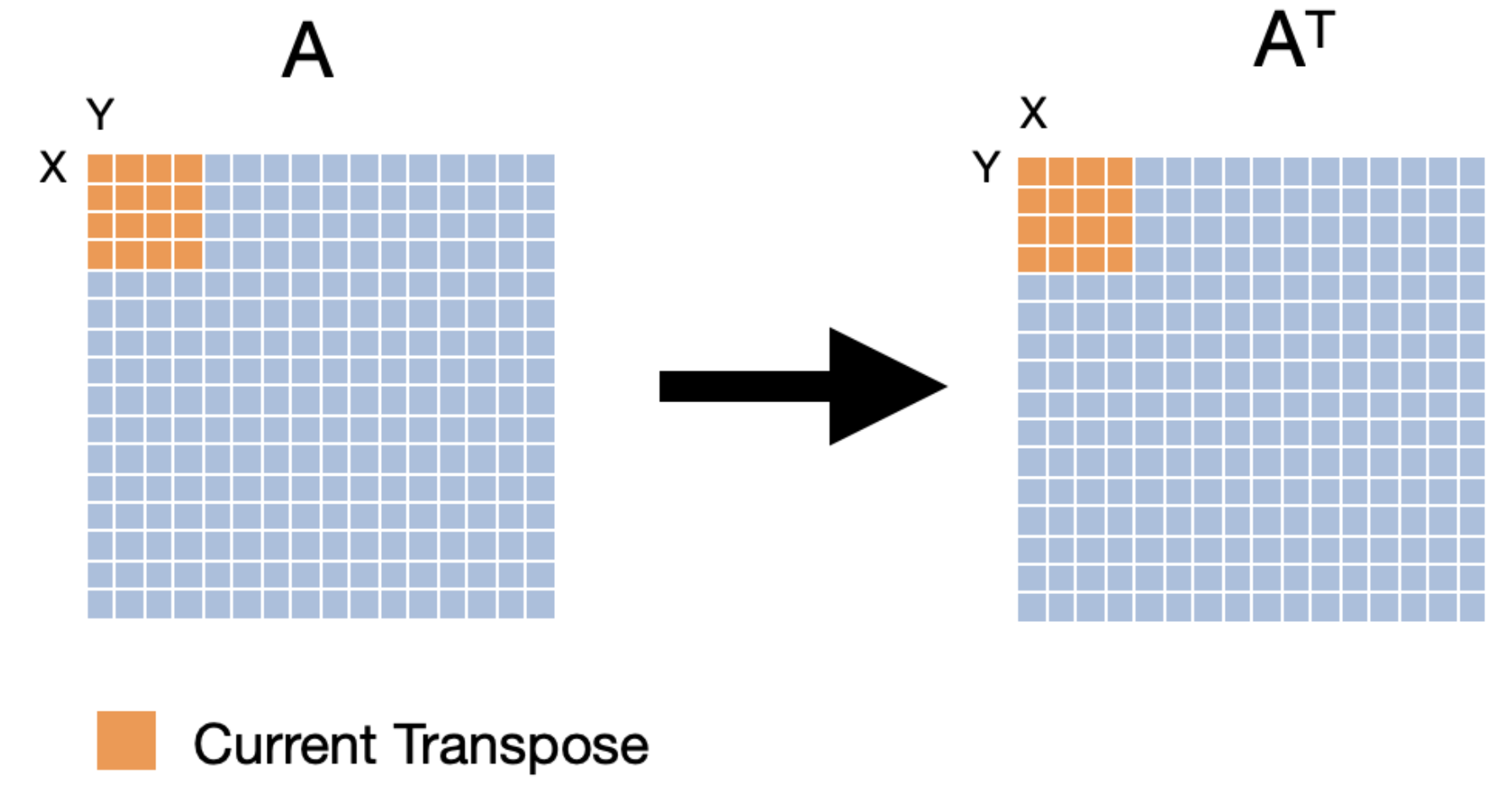
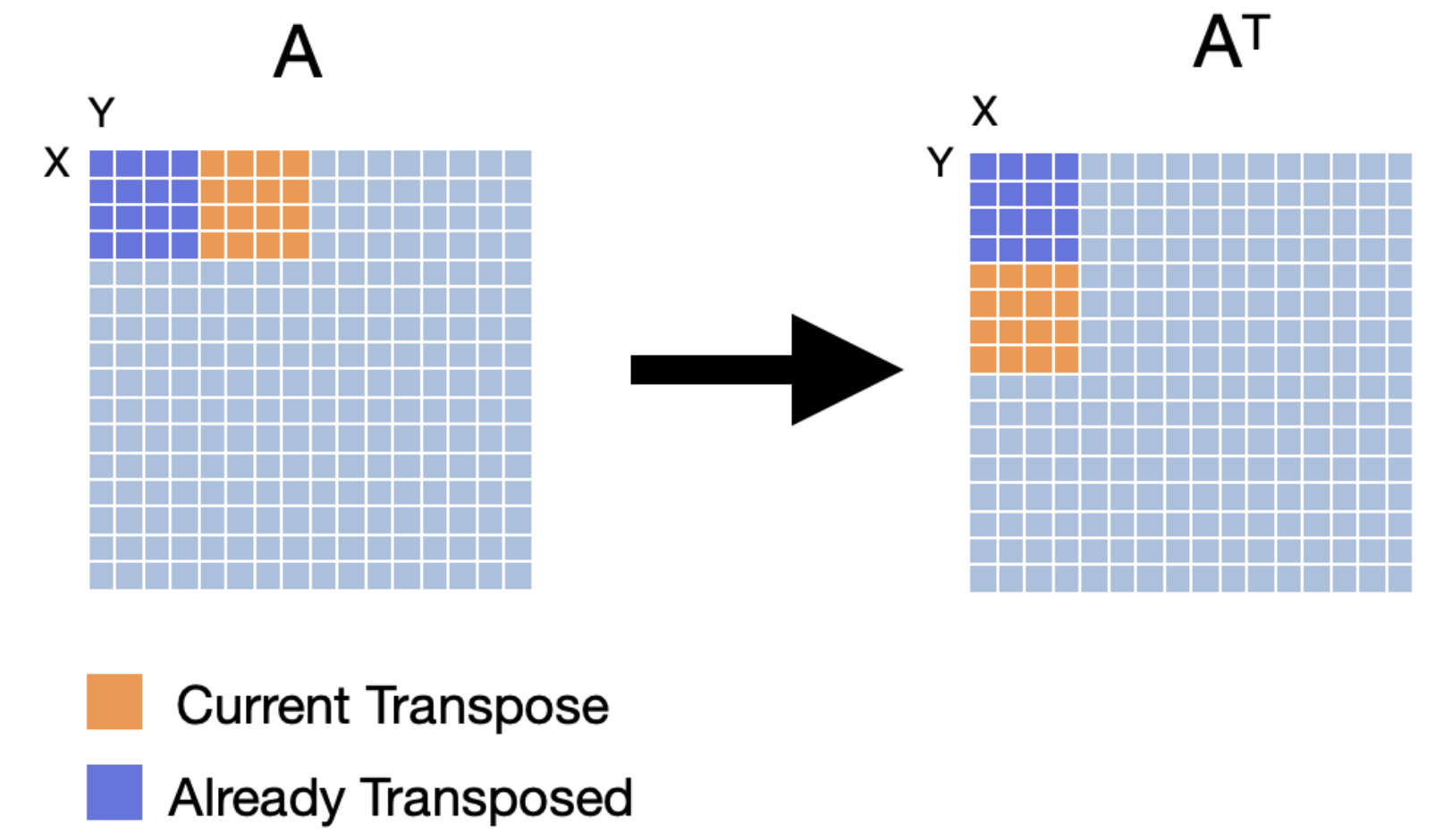
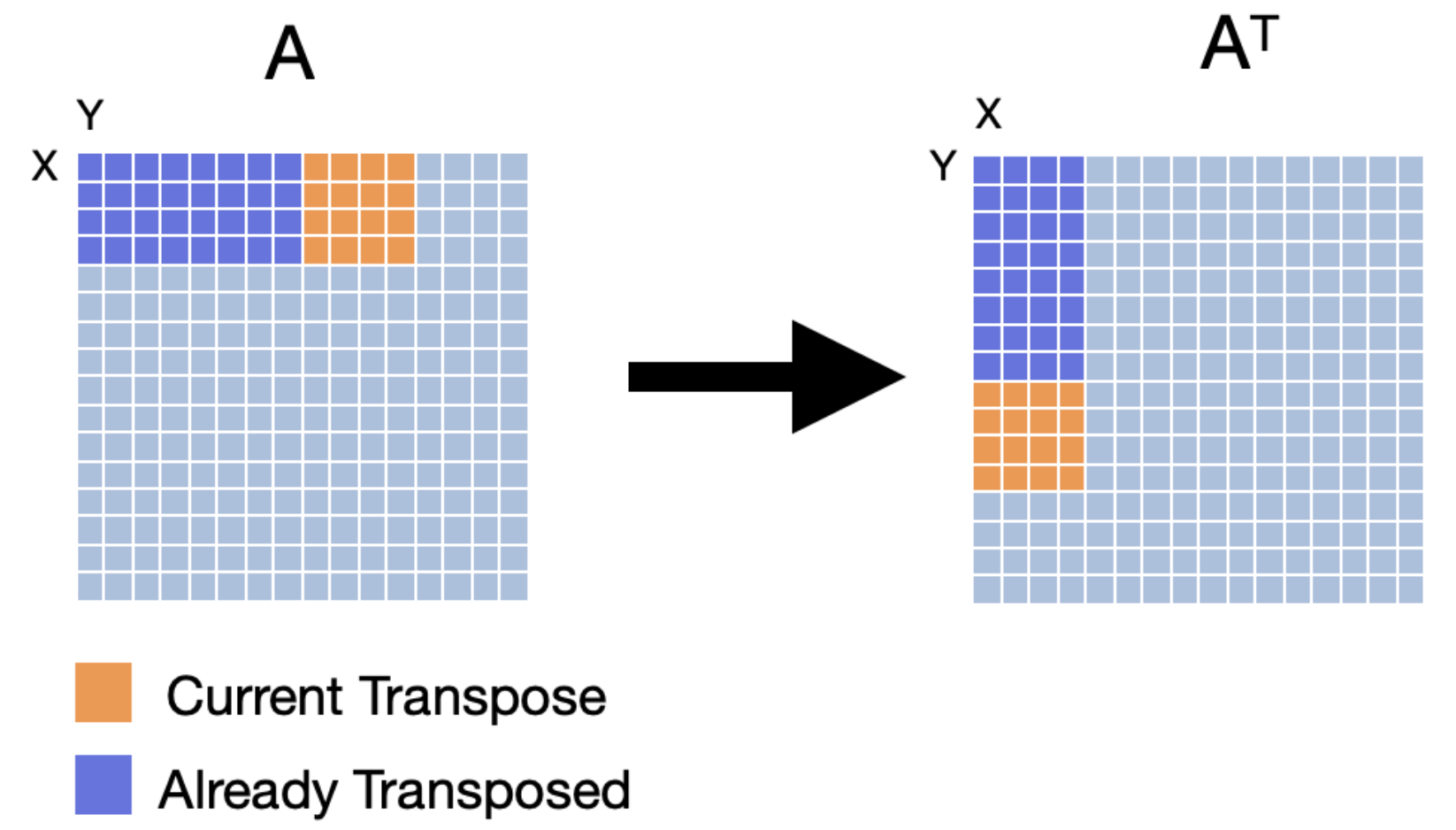
Let's evaluate how cache blocking would perform with the same cache configuration given earlier (fully associative cache with 16 lines and a line size of 16 bytes).

---

---

---

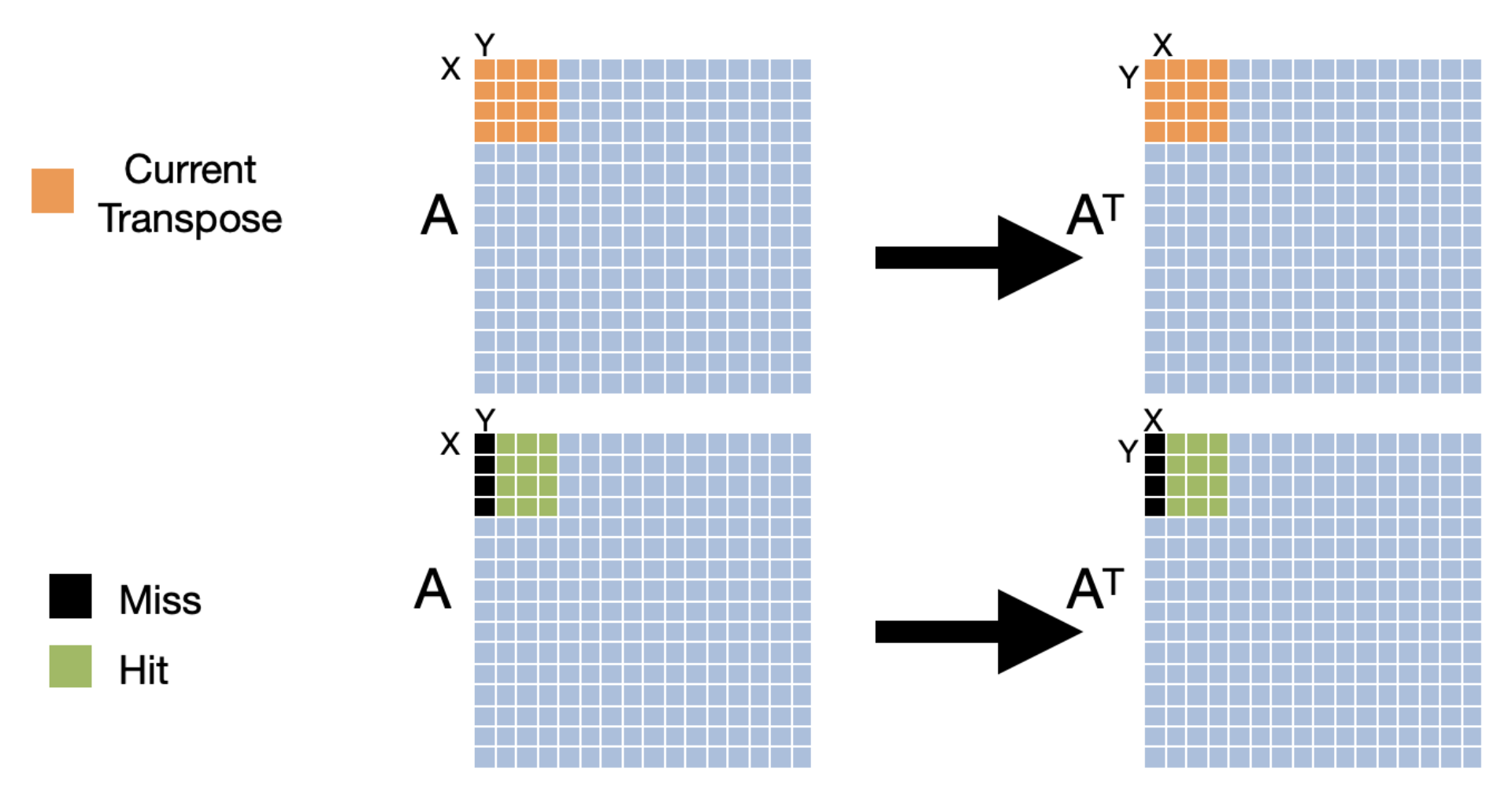
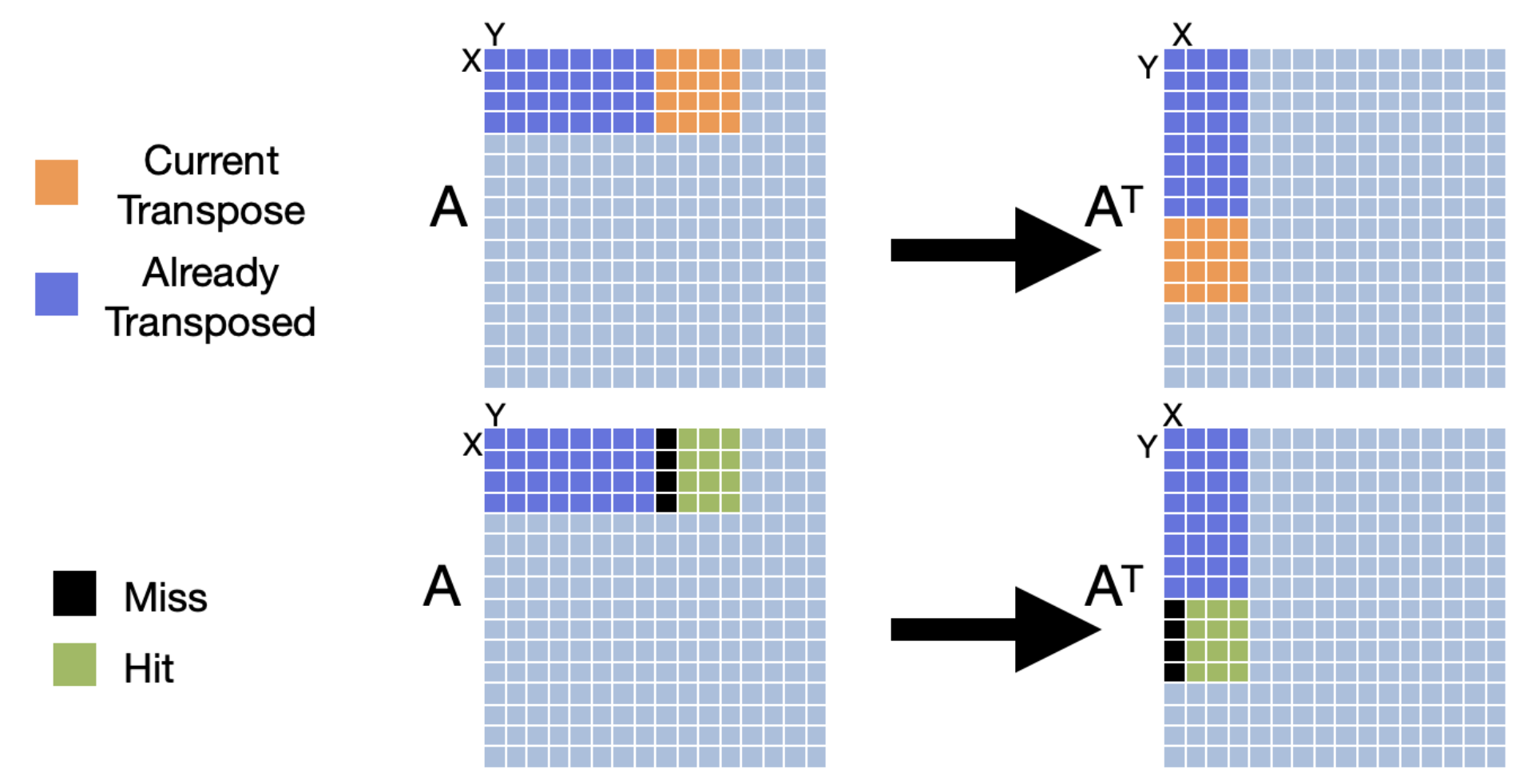
We can see that cache blocking makes much better use of spatial and temporal locality and therefore improves the hit rate of our cache which improves the performance of our program.

Action Item

Your task is to implement cache blocking in the transpose_blocking() function inside transpose.c. You may NOT assume that the matrix width (n) is a multiple of the block size. By default, the function does nothing, so the benchmark function will report an error. After you have implemented cache blocking, you can run your code witht the following:

make ex3
./transpose

You can specify the width of the matrix (n) and the blocksize in test_transpose.c. The default setting is n=12000 and blocksize=80.

Some tips to get started:

Instead of filling out dst one column at a time, we would like to fill out dst square chunks at a time, where each square chunk is of dimension blocksize by blocksize.

We can't assume that n is a multiple of blocksize, so the final block column for each block row will be a little bit cut-off, i.e. it won't be a full blocksize by blocksize square. In addition, the final block row will all be truncated. Make sure that you account for this special case.

Hint: A standard solution needs 4 (four) for loops.

Once your code is working, make sure you can answer the following questions.

Part 1 - Changing Array Sizes

Fix the blocksize to be 20, and run your code with n equal to 100, 1000, 2000, 5000, and 10000.

At what point does cache blocked version of transpose become faster than the non-cache blocked version?

n = 5000, n = 10000

Why does cache blocking require the matrix to be a certain size before it outperforms the non-cache blocked code?

With a bigger matrix size, parts of the matrix can't fit inside the cache, leading to more cache misses from non-blocked code. Blocked code would consolidate accesses to a smaller portion of memory, giving more cache hits. With a smaller matrix size, most of the matrix can probably fit in the cache, so blocking results in more overhead (for loop exits) and doesn't provide a significant increase in cache hit rate.

Part 2 - Changing Block Size

Fix n to be 10000, and run your code with blocksize equal to 50, 100, 500, 1000, 5000.

How does performance change as blocksize increases? Why is this the case?

As the blocksize increases, performance increases until blocksize = 500, then it decreases again.

Why: When the blocksize is too large, the entire block cannot fit inside the cache, negating the advantage of cache blocking. In fact, if the blocksize keeps increasing, we just arrive at the naive approach again.

---

Feedback Form

We are working to improve the labs for next semester, so please fill out this survey to tell us about your experience with Lab 7. The survey will be collecting your email to verify that you have submitted it, but your responses will be anonymized before the data is analyzed. Thank you!

---

Submission

Please submit the Lab 7 Google Form. Then save, commit, and push your work, and submit to the Lab 7 assignment on Gradescope.