TA: DaveJ (cs61c-ta).
Introduction
After a semester of hard work, it's time to put your CS61C skills to the test with a little friendly competition. You will compete with your peers (and maybe even the TAs) to create the world's fastest TacTix solver* ever to run on a Playstation 2. Your adventure will be wrought with danger: stack overflows, perilous segmentation faults, and even the great and terrible combinatorial explosion lie in wait at every turn. But fear not, for you need not embark on this journey alone (partners are allowed and encouraged). Your bravery will be rewarded with vast caches filled to the brim rich with nimsums worth their bits in gold.
*Ok, technically you won't be _solving_ the boards... more on this below.
Background
TacTix is a two dimensional version of the game Nim. Like Nim, two players take turns removing tokens from the board, where the player who takes the last token wins the game. Said another way, if it's your turn, and you have no moves available because the board is empty, you've lost; this is called normal play. Some people play the misere variant, in which the player who takes the last token loses the game. We will only consider normal play for this Performance Contest.
Unlike Nim, however, the TacTix tokens are arranged in a 2D grid rather than a number of heaps. A player may remove any number of tokens from a single row or column, so long as they are contiguous. To get a sense for the game, you can play a Java version of 4x4 misere TacTix. If you want the computer to play first, just click 'move' first. The boards your program will be solving will be much, much bigger.
Project Description
You will be writing a program which computes the nimsum of a TacTix board. A nimsum is a number which sort of represents the good-ness of a board. If you are brave, you can try to work through the wikipedia wisdom to get the theory behind it's meaning. The quick summary is that a winning board has a non-zero nimsum (before you take your turn). Unfortunately, a TacTix nimsum cannot be computed directly as it is in standard Nim; Instead it must be computed through game-tree search. Here is a naive recursive algorithm which computes a board's nimsum:
nimsum(board)
if board is empty
return 0
else
create an empty list sums
for each legal move
generate the child board
add nimsum(child) to sums
return mex(sums)
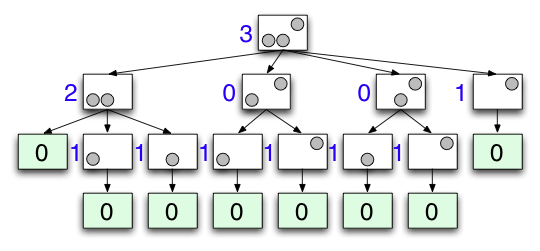
What is this mex business, you ask? Wikipedia again provides an answer, but I'll explain here for your convenience anyway. The minimum excludent (mex) of a set of non-negative integers is the smallest non-negative integer not in the set. So...
mex({0,1,2,5,9}) = 3
mex({1,2,3,...,1000}) = 0
mex({0, 2, 4, 6, ...}) = 1
Here is an example game tree that would be generated by the algorithm presented above. Each gameboard points to its children, all the gameboards resulting from legal moves. The blue numbers next to each non-empty gameboard represent its nimsum, which is calculated by taking the mex of all its children's nimsums. The green boards represent the empty base-case boards. Look carefully for optimizations that could reduce the amount of computation performed.
PBM File Format
Your program's input will be piped in from a portable bit map (PBM) file representing a TacTix board. The output should be the board's nimsum followed by a newline. So a typical run would look like this:% contest < sample1.pbm 1A proper PBM file has three parts: a "magic number" (always the two bytes "P1"), dimensions in pixels (width followed by height), and finally the image data (width*height pixels separated by whitespace, each pixel is a '0' if empty, a '1' if it contains a token). The full PBM specification also allows for comments beginning with '#', but you may safely assume that no board files will contain comments. Here are the contents of a small PBM file to illustrate:
P1 8 4 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 0 1 1 1 0 0 1 0 0 0 0 0 |
becomes |  |
Sample Boards and Nimsums
Here are some example boards with known nimsums. Study these carefully. Also remember that the contest boards may be of any size. The boards shown below were chosen to help understanding and display well on the web.
| Board (click for PBM) | Nimsum |
 |
1 |
 |
1 |
 |
2 |
 |
3 |
 |
4 |
 |
5 |
 |
0 |
 |
3 |
Hint: Think about the connection between TacTix and Nim (HW2). The Sprague-Grundy theorem mentioned above says that any impartial game (like, say, a TacTix subgame) has "grundy number" -- or nimsum -- which is equivalent to a single Nim heap. It also says, just as in HW2, that the "grundy number" of a particular board is the nimsum (read, xor) of the component parts.
For example, consider the following board:

Because each of the three bars is disconnected from the rest (any move that removes tokens from one can't possibly effect the others), they can be solved separately as independent subgames. As the chart above shows, the nimsums of the bars are 2, 3, and 4 starting at the left. You can verify that the nimsum of the complete board is 2 XOR 3 XOR 4 = 5. Finding independent connected components is pivotal in optimizing your solver.
The Playstation 2
We will be running the contest on an actual MIPS machine, specifically a Sony Playstation 2 hidden deep within the bowels of Soda Hall. To login to the ps2, run the command
% ssh-mipsfrom a nova terminal. Since it isn't really meant to be a server, the ps2 hardware probably won't do well with a full class load of logins, so try to edit your files locally or on an instructional machine and connect to the ps2 only for testing. You can transfer files to and from the ps2 by running
% sftp 192.168.128.196from a nova terminal. See the sftp man page for more instructions.
Because the ps2 runs MIPS, you can optimize your code at
the assembly level! If you'd like to hand tune your MIPS,
you can compile to assembly using the gcc -S
flag. Once your finished with your tweaking, you can pass
the *.s files into gcc to be
linked into an executable. You can crank even more power
out of the ps2 by peeking across the ISA boundary.
Technical specifications for the ps2 processor can be found
on
wikipedia.
Official Contest Rules
Each submission will be run on a battery of board configurations with known nimsums. Solvers will be scored and ranked using the following formula:score = # boards correctly solved - # times crashedNote that this means it is very much to your advantage to exit gracefully -- i.e. print a nimsum of -1 or guess -- when your solver fails in computing a nimsum (due to malloc failure, etc.). Ties will be broken by cumulative computation time over all solved boards.
Participation Credit
Participation is entirely optional, but all students who submit a project capable of solving a subset of the contest boards will receive EPA points. In addition, the top three solvers will recieve yet still more EPA points in addition to everlasting fame and glory.
Submission
From your contest code directory, run the command% submit
contest. The only required file is a
README which should contain instructions on
running your submission. If you are working with a
partner, only one of you need submit the assignment, but
be sure to mention both partner's names in the
README. Beyond that, anything is fair game.
In particular, feel free to submit a ps2 executable if
compiling your solver is an especially involved process.