CS61C Spring 2008
Project 02
Structures for MIPS
The TA
in charge:History
- 2008-03-02 19:50:00 Fixed the examples for outputting
infinity in Part 2. The entire word should be lowercase.
- 2008-03-02 15:00:00 Clarified what should happen in the
case of exponent notation with an unbiased exponent of zero for Part 2. In
this case the exponent portion should appear as E0.
- 2008-03-02 14:30:00 IMPORTANT: Updated
file proj2.s to file version 0.04. THIS IS AN IMPORTANT CHANGE. Although
the change is small, it can expose potential bugs in your code that would
NOT have been exposed by the previous file versions. So even if you have
completed Part 1, update your file to version 0.04 and test your code
again. Since the potential bug is related to proper MIPS calling
conventions, it is possible that we may test for it during grading. You
can update your file by backing
up your current proj2.s file, getting the new version, and then copying
any changes you made to the new version.
- Latest File Versions
1. 0.04 proj2.s
: Fixed a bug at the end of the main function that meant that main was
not adhering to the MIPS standard calling conventions as closely as it should
have been. This change can expose potential bugs in your code that previous
versions would not have.
2. 0.02 fp.c
: No change
3. 0.02 test.fp.c
: No change
4. 0.01 Makefile
: No change
5. 0.01 fp.h
: No change
- 2008-03-01
16:45:00 Cleared up what should be done in the case of overflow during
the multiply operation during eval_tree of Part
2. When performing the multiply operation you can simply return the lower
32 bits of the result.
- 2008-03-01
16:30:00 Added a hint as to how to approach the problem presented in the
create_tree function in Part 1. The hint
appears in the description for Part 1.
- 2008-03-01
16:00:00 Fixed the example output in Part 2 sample inputs for input of
0xc900. Value is negative, but example output was missing the negative
sign. Thanks to Paul for pointing this out.
- 2008-02-28 02:00:00 A
clarification was made to Part 1 regarding what constitutes a valid input
string, what kinds of input create_tree may
receive, and what you are allowed to change in proj2.s. This clarification
appears in the description of Part 1 in the same color as this text. Two
small changes were also made to the file for Part 1, updating proj2.s to
file version 0.03. The changes involve declaring the procedures create_tree and eval_tree to
be global (you dont need this, but it will be used for grading), and to
remove some code which ensured that create_tree
would always be called with at least three tokens (this is to prevent some
short, but valid, input strings from being ignored). To update to this
file version you should make a backup of your proj2.s file, copy the new
version to your working directory, and then copy/paste your create_tree and eval_tree
functions (and any added helper functions) into the new file.
- Latest File Versions
1. 0.03
proj2.s : Changed some code in the main procedure
that would zero out the tokens if there were less than three tokens (this was a
mistake). Declared eval_tree and create_tree
to be global (for grading).
2. 0.02
fp.c : No change
3. 0.02
test.fp.c : No change
4. 0.01
Makefile : No change
5. 0.01
fp.h : No change
- 2008-02-26 23:50:00 The requirement changes to Part 2
have been made. The changes include printing denormalized
numbers in the same formats as normalized numbers (instead of just
printing denorm), being able to specify which
of two formats to use (binary point or exponent notation) to print
normalized or denormalized numbers, and a slight
change to the binary point and exponent notation formats (putting 0b
before any number). The file changes include adding fp.h
ver. 0.01, updating test.fp.c to ver. 0.01, and
updating fp.c to ver
0.01. Due to the types of changes made to these files, it is recommended
that if you have any code written for this assignment that you make a copy
of your fp.c file (which is where all of your
code should be), copy over the new files, and then copy/paste your code
from sprint_half into the new fp.c.
- Latest File Versions
1.
0.02 proj2.s : No change
2.
0.02 fp.c : Added an included
header file, changed sprint_half signature.
3.
0.02 test.fp.c : Added an
included header file, changed all test calls to match new requirements.
4.
0.01 Makefile
: No change
5.
0.01 fp.h : New file, includes
definition of enum format_t
type, and the new prototype of sprint_half.
- 2008-02-26 22:05:00 There are two big changes that are going
to be made to Part 2 (floating point in C). We apologize for making these changes
after the project has gone live, but you will be responsible for the
updated requirements. Since the changes havent been made yet, you may
want to hold off on starting Part 2. The changes wont require you to
throw away any code you may have already written, but they will change the
final output. The changes will be explicitly spelled out on this page once
they have been finalized.
- 2008-02-26
22:00:00 Ensured homogeneity in example tree diagram (made all operation
nodes have op. in the Token field).
- 2008-02-26
01:37:00 The testing code for Part 1 has been completed. It is file
proj2.s, version 0.02. If you have version 0.01 of this file, back it up,
get the new version, then copy any changes you
made to the new version.
- Latest File Versions
1. 0.02 - proj2.s
2. 0.01 fp.c
3. 0.01 test.fp.c
4. 0.01 - Makefile
- 2008-02-25
23:12:30 Project 2 released.
- Note that at this point the
provided code for Part 1 is not yet ready. You can begin looking it over
to get an idea of how some of the data types look, but you should be
aware that the file will need to be updated very soon.
Note that if any students are having
a hard time reading any of this web page for any reason (font too small, the
font colors are difficult to read, etc.), that you may contact the TA in charge
(listed above) and they can provide you with a version of this web page that is
easier to read.
Purpose
Gain experience with:
- MIPS
calling convention,
- recursive
functions in MIPS,
- floating
point representation
and generally become an all-around totally awesome assembly
programmer.
Instead of one big, long, crazy project, you
will do two smaller, shorter, sane sub-projects.
Getting Started
Copy them from ~cs61c/proj/02 by typing the following:
cp -r ~cs61c/proj/02 ~/proj
This copies two files you will turn in (proj2.s, fp.c) as well as a Makefile, a
header file, and corresponding test harnesses for each of the files you will
turn in.
Submission
To submit your project, create a directory named proj2
that contains: proj2.s and fp.c. From within that directory, type "submit proj2".
The project deadline is 11:59:59pm on Wednesday, March
5th, 2008.
Part 1: Expression Trees in
MIPS
The
provided code for Part 1 is now ready. It is version 0.02 of file proj1.s.
The goal of this
assignment is to evaluate a string representing a series of arithmetic operations.
Each of the operations in the string consists of an arithmetic operation, and
exactly two arguments to that operation, with spaces separating each. A simple
example of such a string is + 1 2, which represents adding together the
numbers 1 and 2. This is simple enough for calculations that have only one
operation, but can quickly become very complex for calculations with many
operations. For instance, if we wanted to multiply the results of two sums, the
string would look something like the following: * + 1 2 + 3 4. We could make
an even more complex operation which would give the square of the preceding
example, which would look like: * * + 1 2 + 3 4 * + 1 2 + 3 4. As you can
see, even with only six operations, the string quickly becomes difficult for a
human to read. A computer, on the other hand, has no trouble understanding the
string, since it follows a strict set of rules.
The rules are as
follows:
1. There are 6 types of operations, addition (+), subtraction
(-), multiplication (*), integer division (/), binary (logical) AND (&),
and binary (logical) OR (|).
2. Each operation takes exactly two numbers as arguments, and
returns the result of performing the appropriate operation on those arguments.
3. Any argument to an operation can be replaced with another
operation, and the result of the inner operation should be used as an argument
of the outer operation.
These rules
result in a format that is almost exactly like Scheme arithmetic operations. If
you were to take a series of Scheme operations using only adds, subtracts,
multiplies, and divides, then restrict the operations to only take two
arguments, and you were to remove the parentheses, you would have a string
matching our requirements. Example: A Scheme operation of (+ 1 (* 2 (- 3 4)))
would become + 1 * 2 3 4 in our representation.
The goal of this
assignment will be to create a way to evaluate expressions of the above type
using MIPS. The solution will involve three steps. The steps are:
1. Parse the operation string into a format more suitable for
computing.
2. Transform the parsed string into an expression tree. An
expression tree is simply a binary tree where each node holds either an
operation, or a number. If the node holds a number, then both the left and
right children are null. If the node holds an operation, then its left and
right children are pointers to nodes which hold the arguments to the operation.
This is a particularly nice representation for our problem because it can be
built, and operated on via recursive functions.
3. Once the expression tree has been built we can use it to
evaluate the entire expression. This is done by traversing down the tree
recursively. We dont do any processing on our way down the tree. Instead, all
of the processing is done on our way back up the tree. As we return upwards we
return either the value of the number stored at that node, or the value of
performing the specified operation at that node. This is basically a post-order
traversal of the tree, since if we are at a number, there are no children to
visit, and if we are at an operator, we visit both children to get the argument
values before performing the appropriate operation.
Luckily for you,
Step 1 will be taken care of for you. You will be provided with a function that
will parse the operation string into a particular data representation. This
data representation will be a token that is 32-bits long, with the first 8 bits
being the operation/number indicator, and the remaining 24 bits representing a
24-bit twos-complement signed number. The representation appears below:
|
Fields: |
Operation/Number Indicator |
Number Field |
|
Width
in bits: |
8 |
24 |
The
operation/number indicator will be equal to zero if the token represents a number.
If the token represents an operation, then the number field will be equal to
zero, and the operation/number indicator will be equal to a specific ASCII
value of a character that is commonly used to represent that operation. The
full list of possible operation indicators appear in the table below:
|
8-bit
Operation Indicator |
Meaning |
|
0 |
Token is a number, stored in the 24-bit number field |
|
0x2b (+) |
Addition |
|
0x2d (-) |
Subtraction |
|
0x2a (*) |
Multiplication (if any overflow
occurs, simply return the lower 32 bits of the result) |
|
0x2f (/) |
Division (Integer Division Only) |
|
0x26 (&) |
Binary (Logical) AND |
|
0x7c (|) |
Binary (Logical) OR |
For Step 2, you will
be writing a function (create_tree) that will take a
variable number of arguments and use the above token format to build an
expression tree. The expression tree will consist entirely of nodes which
contain three elements. The first element will be a token of the format
described above. The second and third elements will be pointers to other nodes
(left and right children). Note that the first element must be at the lowest
address of the three elements. For example, if the node is located at address 0x10000000,
then the token must also be at address 0x10000000, and the child pointers must
be at addresses 0x10000004 and 0x10000008.
The goal of your
function create_tree for this step will be to take in
all of the tokens (and a count of how many tokens there are) as a variable
number of arguments, dynamically allocate memory for each node, build the
expression tree, and then return the address of the root node. The arguments to
create_tree will be a count of all of the tokens in
$a0, the first three tokens in $a1-$a3, and the rest of the remaining tokens,
if there are any, will be passed on the stack. The tokens on the stack will be
in order, with the fourth token at address 0($sp), the fifth at 4($sp), etc.,
where $sp is the address in the $sp register when your create_tree
function is called. If you need help understanding variable numbers of
arguments, check out this tutorial from the Spring
2007 semester.
Note that if create_tree is called when there are no tokens that the
first argument (the token count) will be equal to zero. If this occurs, then
there is no tree to be created. In this case create_tree
should return NULL (a pointer equal to zero).
You will be
dynamically allocating memory for all of the nodes in memory using a MARS syscall. To do this, put the number of bytes you want to
allocate into $a0, put the number 9 into $v0, and then use the instruction syscall (without the quotes). The address of the allocated
memory will be returned in $v0. Since MARS does not have a way to free
allocated memory, there will be no requirement for you to deallocate
any memory. An example on how to allocate memory in MARS:
li
$a0, 8 # allocate 8 bytes
li
$v0, 9 # set the appropriate syscall code
syscall
# use the address in $v0 to access the
allocated memory
To build the tree you should process one
token at a time. Each time you process a number token you simply create a new
node, place the token inside it, and set the two child pointers to NULL (zero).
More difficult is to process operator tokens. To process an operator token, you
should create a new node, place the token inside that node, and then set the
child pointers. To set the child pointers you must process the token
immediately following the operator token, and set the left child pointer to
point to that created node. Note that this a recursive process, since the token
you process to set the left child can be another operator token. The recursion would
end when an operator token is followed by two number tokens (this is guaranteed
to happen in our specification). Once the recursion has finished for the left
child, then you repeat the same process to set the right child.
To help you understand the process, here
is a diagram of the tree resulting from the operation string + * 1 2 3 / 4
5:
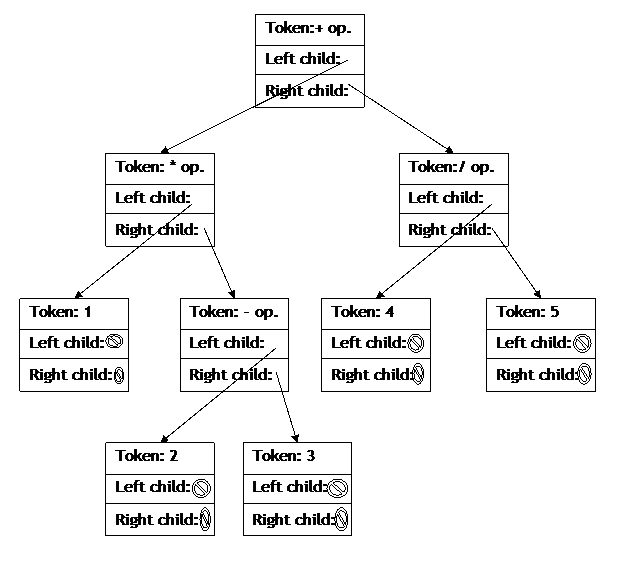
The last step will require you to write
the function eval_tree. This function (WHICH MUST
BE RECURSIVE), will take in a pointer to an expression tree, and will return a
32-bit twos complement signed integer which is the result of computing all of
the operations in the operation string on the appropriate arguments. This is done by traversing down the tree recursively. We
dont do any processing on our way down the tree. Instead, all of the
processing is done on our way back up the tree. As we return upwards we return
either the value of the number stored at that node, or the value of performing
the specified operation at that node. This is basically a post-order traversal
of the tree, since if we are at a number, there are no children to visit, and
if we are at an operator, we visit both children to get the argument values
before performing the appropriate operation. If eval_tree
is passed a NULL pointer as its argument, it should return zero.
Here
are some clarifications about what constitutes a valid input string, and what
kind of input to create_tree can be expected in those
cases. A valid input string can have zero or more operators. Any operator in
the input string must have exactly two arguments, which can be either a number
or the result of another operator. Note that you do not need to handle invalid
input strings. Below are some examples of some valid and some invalid input
strings, and how they should be handled.
|
Example Input String |
Valid or Invalid |
How it should be
handled |
|
an empty string |
Valid |
An
empty string will result in zero tokens. Your create_tree
function should return a NULL pointer (equal to zero). Your eval_tree function should return zero when given a NULL
pointer. |
|
5
a string with a single number |
Valid |
In
this case create_tree will be given only one token,
which should be used to create a tree consisting of a single node. |
|
+
string with an operator but without the required two arguments |
Invalid |
Nothing,
you are not expected to handle any invalid input strings. |
|
+
1 2 string with an operator and exactly two arguments |
Valid |
This
is the shortest valid input string with at least one operator. You should
handle it normally. |
You should write your create_tree
and eval_tree functions in the file proj2.s. You can write
as many helper functions as you want, but eval_tree must
be recursive. You should not change anything above the declaration of create_tree, and you should not add any global variables.
Anything you write should be called (either directly or indirectly) by either create_tree or eval_tree.
When writing your code, remember that the readers will be reading your
code. In order to make sure that the readers have the best opportunity for
ensuring that your code works, you should make sure that your code is easy to
read. A good style for MIPS code is to group all the instructions to accomplish
a task into small sections, and place a comment before each section describing
what that section does. It is also helpful to place comments are every
instruction or two describing what those instructions are doing. Another
helpful thing is to give register values more meaningful variable names in your
comments.
We have
realized that some students may have trouble seeing the most natural algorithm
for writing the create_tree function. Since a lot
of this confusion may be related to a lack of familiarity with binary tree
algorithms, we have decided to give a hint to get students started.
Most functions that take in a variable
number of arguments are not themselves recursive. The reason for this is what a
lot of students have already realized: the work needed to prepare the remaining
arguments for a recursive call is too great. So most functions that take in a
variable number of arguments actually involve a loop, which iterates over each
of the variable arguments, and which processes one argument at a time. Your create_tree function can do this same thing, but in order
to see how it can be done you must notice a particularly nice property of the
trees that we are creating. It turns out that it is possible to start with a
partially complete expression tree, and then find the correct spot to fill the
next node in the tree without having to know where the next spot is ahead of
time. This means that given a partially complete expression tree, you can begin
traversing it from the root node, and successfully find the correct place to
add the next node. This allows create_tree to simply
iterate over all of the tokens (switching between registers and the stack when
needed) and simply pass each token to a helper function which will iterate the
tree-so-far, insert the new node where it should go, and then return.
If you cant easily figure out how the
traversal for inserting into a tree should work, you can work out a few simple
examples by hand, trying different traversal orders to see which produce
expression trees that look right. A few good examples are + 1 2, + * 1 2 3,
+ 1 *2 3, and + * 1 2 * 3 4.
Part 2: Floating Point
The requirements for this part of
the project have changed since it was first put on this site. The relevant
changes have been highlighted in red text. The files for this part of the
project have been updated to match this spec. This includes adding the file fp.h file version 0.01, updating fp.c to file version 0.02, and updating test.fp.c
to file version 0.02.
Fill in the C function:
void sprint_half(char* outbuf, uint16_t f, enum format_t format)
The data type format_t
is an enumerated data type with two possible values (BINARY_POINT and
EXPONENT_NOTATION). The two possible values will indicate which output format
to use when handling denorms or regular normalized
floats.
The function should write into outbuf a string corresponding to interpreting f as an
IEEE 754r 16-bit floating point number (a.k.a. half-precision float) using the
guidelines below. You may assume that outbuf already has enough space allocated to hold your output.
Put your code in the framework in fp.c. Sample test code is provided in test.fp.c. You can compile and execute your code under the
sample test bench by using the Makefile by typing "gmake fp".
Recall that uint16_t is the C99 16-bit unsigned int type. We use this to guarantee a type that is exactly
16 bits, even though we will not be treating the number as an integer.
Format of IEEE 754r half-precision float:
|
Fields: |
Sign |
Biased
Exponent (Bias of 15) |
Significand
Expression |
|
Width in bits: |
1 |
5 |
10 |
Print it out according the format specified below:
- If the format parameter is equal
to EXPONENT_NOTATION, print the normalized or denormalized number in
format: [-]0b1.ddddddddddE[-]xxxx where
1.dddddddddd is the mantissa represented in binary (note the leading 1),
E stands for Exponent (where the right side is the power of 2 to multiply
the mantissa by - recall scientific notation), and xxxx
is the (unbiased) exponent in binary. If the mantissa
is 1.0, print out 0b1.0E[-]xxxx. You should not have any leading 0's on the
exponent or trailing 0's on the mantissa, except for the case where the
mantissa is 1.0. Note that if the unbiased
exponent is equal to 0 (zero), then the exponent portion should appear as
E0, which is a capital letter E, and the digit zero.
o
A bit of
clarification on biased vs. unbiased:
- BIASED EXPONENT - The exponent that is stored
in the bits of an IEEE 754r floating point number.
- UNBIASED EXPONENT - The number x in the
expression 2^x. That is, the actual "mathematical"
exponent in scientific notation.
- In other words, the unbiased
exponent is less than the biased exponent
- Unbiased exponent = biased
exponent exponent bias
- One more item: Remember for
this portion of the assignment, that we are dealing with half-precision
floating points - 16 bit floating point numbers.
- If the format parameter is equal to BINARY_POINT, print the number as: [-]0bmmmmmm.dd...d, where mmmmmm is the whole number part of the float and ddd...d is the fractional part. Both are in binary.
Do not have any trailing or leading zeroes, except for those used to
indicate a whole or fractional part that is equal to zero. If the whole
part is equal to zero (meaning that the entire number is fractional), the
format should be [-]0b0.ddddddd...d.
If the fractional part is 0, the format should be [-]0bmmm...m.0
- In
both cases, the '-' is printed if the number is negative. Leading zeros
are not printed, except as indicated previously.
- Handle
zero, infinity, and NaN as shown below in the
table, where [-] means that you should place a minus sign into the buffer
at that position if the number has the sign bit set, and you should not
place a minus sign into the buffer if the sign bit is not set. The
brackets are merely to indicate that the sign bit is conditional. No
brackets should ever appear in your results.
- Note that the revised specification requires you to produce
output for denorms that is in the same format as
normalized numbers.
The following table lists all the floating point
possibilities:
|
Half Precision |
Object Represented |
What you must write into the
buffer |
|
|
Exponent |
Mantissa |
||
|
0 |
0 |
zero |
[-]0 |
|
0 |
nonzero |
± denormalized
number |
This requirement was
changed 2008-02-26 23:50:00 [-]mantissa_in_binaryE[-]exponent_in_binary |
|
1-30 |
anything |
± normalized number |
[-]mantissa_in_binaryE[-]exponent_in_binary |
|
31 |
0 |
± infinity |
[-]infinity |
|
31 |
nonzero |
NaN (Not a Number) |
[-]NaN |
Sample cases:
|
Value of f in Hexadecimal |
Value of f in Decimal |
What gets written into the buffer (format ==
BINARY_POINT) |
What gets written into the buffer (format == EXPONENT_NOTATION) |
|
0x fc1a |
N/A |
-NaN |
-NaN |
|
0x 7c00 |
Infinity |
infinity |
infinity |
|
0x 0001 |
2^-24 |
0b0.000000000000000000000001 |
0b1.0E-11000 |
|
0x 8000 |
0 |
-0 |
-0 |
|
0x 3455 |
|
0b0.010001010101 |
0b1.0001010101E-10 |
|
0x c900 |
10 |
-0b1010.0 |
-0b1.01E11 |
|
0x 8400 |
-2^-14 |
-0b0.00000000000001 |
-0b1.0E-1110 |
Things to keep in mind
- Obey all register conventions in this project: return the return value of any function that has one
in $v0 and do not use $sx registers
without saving them first. In particular, remember that the $ax
registers are temporary registers, so they will be clobbered by any
function call. Points will be deducted for
violations of these conventions. Your procedures must work with the main
function of any testing program that confirms to this specification, and
not just the test one provided to you. Also, bear in mind that our autograder assumes that your function
obey register conventions (and might just test for it!).
- You must comment your MIPS code. The graders will read it, and they need to be able to
quickly understand what every section does. A common style for commenting
assembly is to include a long introductory comment before every block of
assembly statements, with a short comment after every line telling what it
does. The introductory comment must describe the algorithm that the
following block implements. The line-by-line comments must just be an easy-to-read
version of the assembly code, using real variable names and perhaps more
C-like constructs. If your code ends up being at least as much comment as
code, this is probably a sign that you are doing a good job of commenting.
- Minimum-Effort Digit Formatting: For all the number formatting cases, you must
minimize the number of digits your function prints. This means that you
should not print leading zeros, or any trailing
zeros after a floating point unless the entire portion after the floating
point is equal to zero. In the case of the entire portion after the
floating point being zero, you should print that portion as .0.
- Use breakpoints to debug your MIPS code. MARS is not only a MIPS R2000 interpreter,
it is also a debugger as well. Thus, it is to your advantage to use MARS'
debugging functions, especially its breakpoint functionality.
- Build incrementally. You should build up your MIPS code gradually by
implementing one element of your code one at a time instead of all at
once. This will save you time debugging and perhaps your sanity.