Click here for a list of the changes


NOTE: right now ppmtogif and display are only available on the solaris machines. If you would like to try out those programs (which is not required to do the assignment), log into nova.cs.berkeley.edu.
You are to implement a one-dimensional variant of Conway's Game of Life, heretofore called "Life 1D". Specifically, you will write the following program in C (from scratch) which supports the following:UPDATE: the usage string we would like your program to print is:
Usage: Life1D <rows> <rule>We are including the older version here so you may reference the program behavior it describes.
Usage: Life1D <rows> <rule>
This program simulates 1D Life: the simplest class of one-dimensional
cellular automata in a <ROWS=rows+1> x <COLS=2*rows+1> grid starting
with a single live cell in the middle of the top row using rule <rule>.
These 1D rules are defined in Wolfram's Elementary Cellular Automata:
http://mathworld.wolfram.com/ElementaryCellularAutomaton.html
This program will print to stdout data in plain PBM file format.
This output can be easily viewed using the display command or
converted to a another format using the pbmto* and ppmto* utilities.
A plain ascii PBM file can be created by adding a header line
"P1 <WIDTH> <HEIGHT>" and followed by a grid of data
(0 = dead = white, 1 = live = black). Add a comment on the first
line with a brief description of the image.
Arguments:
<rows> is a positive integer specifying the number of rows to generate
(not counting the first "seed row" which is all dead except for a central
live cell). The columns are computed automatically -- enough so that
the rule, if it were to grow in the normal triangular pattern, would
just perfectly reach the edge. Off the board is considerered "dead".
<rule> is a number from 0-255 specifying the rule to use.
Examples:
See Rule 60 : http://mathworld.wolfram.com/Rule60.html
unix% Life1D 3 60
P1 7 4 ## 3 rows of Life1D (Rule 60) by Yourfirstname Yourlastname
0 0 0 1 0 0 0
0 0 0 1 1 0 0
0 0 0 1 0 1 0
0 0 0 1 1 1 1
See Rule 90 : http://mathworld.wolfram.com/Rule90.html
unix% Life1D 5 90
P1 11 6 ## 5 rows of Life1D (Rule 90) by Yourfirstname Yourlastname
0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 1 0 1 0 0 0 0
0 0 0 1 0 0 0 1 0 0 0
0 0 1 0 1 0 1 0 1 0 0
0 1 0 0 0 0 0 0 0 1 0
1 0 1 0 0 0 0 0 1 0 1
See Rule 250 : http://mathworld.wolfram.com/Rule250.html
unix% Life1D 4 250
P1 9 5 ## 4 rows of Life1D (Rule 250) by Yourfirstname Yourlastname
0 0 0 0 1 0 0 0 0
0 0 0 1 0 1 0 0 0
0 0 1 0 1 0 1 0 0
0 1 0 1 0 1 0 1 0
1 0 1 0 1 0 1 0 1
$ Life1D 17 139 P1 35 18 ## 17 rows of Life1D (Rule 139) by cs61c 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 0 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0However, the images at Mathworld suggest that it should be like this:
$ Life1D 17 139 P1 35 18 ## 17 rows of Life1D (Rule 139) by Mathworld 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1Can you spot the difference? The cs61c solution has several diagonals of zeros while the Mathworld solution does not. This is due to Mathworld assuming the grid is an infinite grid (versus a finite grid in this assignment). Therefore, for the sake of simplicity, the cs61c solution is considered the "correct" solution for this assignment. This means, you do not need to write additional C code to produce the Wolfram solution. For those of you who want to have a more "correct" solution, see the Extra for Experts Section.
P1 [a] [b] ## [c] rows of Life1D (Rule [d]) by [e]where [a] is the number of displayed cols, [b] is the number of displayed rows, [c] is the <row> parameter. [d] is the <rule> parameter, [e] is your name
000010000 000010100 000010010and this is valid:
0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 1 0 0 1 0
unix% Life1D 3 60 | ppmtogif > Life1D_3_60.gifHere are the gifs resulting from the examples above:
 Life1D 3 60 | 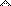 Life1D 5 90 |  Life1D 4 250 |
% Life1D 17 139 ;; would produce the cs61c solution % Life1D 17 139 Wolfram ;; would produce the image that matches the websiteIf you really enjoy this project, you might want to consider implementing a Totalistic Cellular Automaton, otherwise known as "Life1D in grayscale/color". Enjoy!