Image Compression via Least-Squares

We can use least-squares to represent an image in terms of a linear combination of ‘‘basic’’ images, at least approximately.

An image can be represented, via its pixel values or some other mechanism, as a (usually long) vector 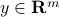$y in mathbf{R}^m$ . Now assume that we have a library of 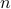‘‘basic’’ images, also in pixel form, that are represented as vectors 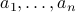a_1,ldots,a_n . Each vector 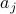a_j could contain the pixel representation of a unit vector in some basis, such as a two-dimensional Fourier basis; however, we do not necessarily assume here that the 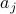a_j 's form a basis.

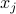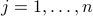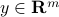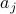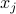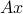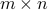Let us try to find the best coefficients x_j , j=1,ldots,n , which allow to approximate the given image (given by $yinmathbf{R}^m$ ) as a linear combination of the a_j 's with coefficients x_j . Such a combination can be expressed as the matrix-vector product , where A = [a_1, ldots, a_n] is the mtimes n matrix that contains the basic images. The best fit can be found via the least-squares problem

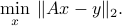
Once the representation is found, and if the optimal value of the problem above is small, we can safely represent the given image via the vector . If the vector is sparse, in the sense that it has many zeros, such a representation can yield a substantial saving in memory, over the initial pixel representation .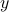

The sparsity of the solution of the problem above for a range of possible images 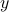is highly dependent on the images’ characteristics, as well as on the collection of basic images contained in . In practice, it is desirable to trade-off the accuracy measure above, against some measure of sparsity of the optimal vector .