Solving triangular systems of equations: backwards substitution example

Consider the triangular system

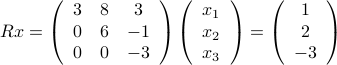
$Rx = left( begin{array}{ccc}3&8&30&6&-10&0&-3end{array}right) left( begin{array}{c}x_1x_2x_3end{array}right) = left( begin{array}{c}12-3end{array}right)$

we solve for the last variable 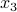x_3 first, obtaining (from the last equation) 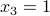x_3 = 1 . We plug this value of 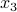x_3 into the first and second equation, obtaining a new triangular system in two variables x_1,x_2 :

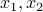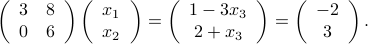
$left( begin{array}{ccc}3&80&6end{array}right) left( begin{array}{c}x_1x_2end{array}right) = left( begin{array}{c}1-3x_32+x_3end{array}right) = left( begin{array}{c}-23end{array}right).$

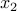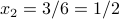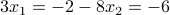We proceed by solving for the last variable x_2 . The last equation yields x_2 = 3/6=1/2 . Plugging this value into the first equation gives 3x_1 = -2-8x_2 = -6 .

We can apply the idea to find the inverse of the square upper triangular matrix 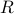, by solving

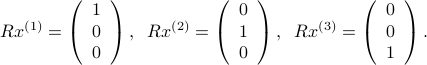
$Rx^{(1)} = left(begin{array}{c}100end{array}right) , ;; Rx^{(2)} = left(begin{array}{c}010end{array}right) , ;; Rx^{(3)} = left(begin{array}{c}001end{array}right) .$

The matrix $[x^{(1)},x^{(2)},x^{(3)}]$ is then the inverse of 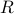. We find

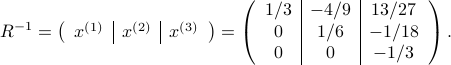
$R^{-1} = left( begin{array}{c|c|c} x^{(1)} & x^{(2)} & x^{(3)} end{array} right) = left( begin{array}{c|c|c} 1/3 &-4/9&13/27 0&1/6&-1/18 0&0&-1/3 end{array} right) .$

As illustrated above, the inverse of a triangular matrix is triangular.