Optimality Conditions and Sensitivity
Complementary slackness
KKT optimality conditions
Primal solutions from dual variables
Examples
Complementary slackness
We consider a primal convex optimization problem (without equality constraints for simplicity):
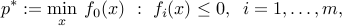
and its dual
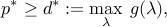
where 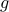 is the dual function
is the dual function
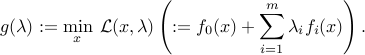
We assume that the duality gap is zero: 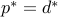 , and that both primal and dual values are attained, by a primal-dual pair
, and that both primal and dual values are attained, by a primal-dual pair 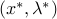 . (This is guaranteed for example if both the primal and dual are strictly feasible, in the weak sense of Slater’s.) We have
. (This is guaranteed for example if both the primal and dual are strictly feasible, in the weak sense of Slater’s.) We have
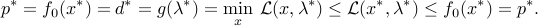
Thus, equalities hold in the above.
This implies that 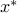 minimizes the function
minimizes the function 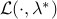 :
:

If the functions 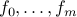 are differentiable, the above implies
are differentiable, the above implies
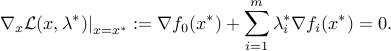
In addition, the equalities in (ref{eq:root-KKT-conds-L15}) imply
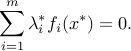
Since 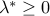 ,
, 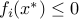 ,
, 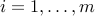 , the above is equivalent to the complementary slackness condition:
, the above is equivalent to the complementary slackness condition:
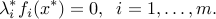
KKT optimality conditions
Assume that the functions 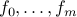 are differentiable.
are differentiable.
Consider the so-called KKT (The acronym comes from the names Karush, Kuhn and Tucker, researchers in optimization around 1940-1960) conditions on a primal-dual pair 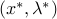 .
.
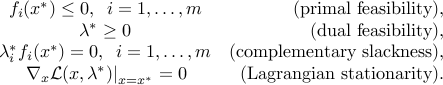
The above development shows that for any problem (convex or not) for which strong duality holds, and primal and dual values are attained, the KKT conditions are necessary for a primal-dual pair 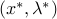 to be optimal.
to be optimal.
If, in addition the problem is convex, then the conditions are also sufficient. To see this, note that the first two conditions imply that 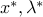 are feasible for the primal and dual problems, respectively. Since
are feasible for the primal and dual problems, respectively. Since 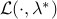 is convex, the fourth condition (which we called Lagrangian stationarity) states that
is convex, the fourth condition (which we called Lagrangian stationarity) states that 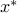 is a minimizer of
is a minimizer of 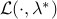 , hence
, hence
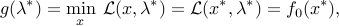
where we used the third condition (complementary slackness) for the last equality. The above proves that the primal-dual pair 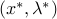 is optimal, since the corresponding gap is zero.
is optimal, since the corresponding gap is zero.
Primal solutions from dual variables
Assume that the problem has a zero duality gap, with dual values attained. Now assume that 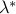 is optimal for the dual problem, and assume that the minimization problem
is optimal for the dual problem, and assume that the minimization problem
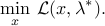
has a unique solution 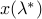 that is feasible for the primal problem. Then,
that is feasible for the primal problem. Then, 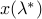 is optimal. Indeed, the fourth KKT condition (Lagrange stationarity) states that any optimal primal point minimizes the partial Lagrangian
is optimal. Indeed, the fourth KKT condition (Lagrange stationarity) states that any optimal primal point minimizes the partial Lagrangian 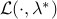 , so it must be equal to the unique minimizer
, so it must be equal to the unique minimizer 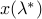 .
.
This allows to compute the primal solution when a dual solution is known, by solving the above problem.
Examples
XXX