Geometric View of Weak Duality
Two-dimensional view of the primal problem
Let us assume for simplicity that  , and consider the problem:
, and consider the problem:

(In fact, this can be done without loss of generality, using the pointwise maximum of the constraints as a single constraint.)
To illustrate, we focus on the problem above, with  defined as
defined as


We can express the primal problem with two new scalar variables  , as follows:
, as follows:

where

The set  can be interpreted as the set of constraint / objective pairs
can be interpreted as the set of constraint / objective pairs  that can be achieved by some choice of the original decision variable
that can be achieved by some choice of the original decision variable 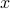 . The set
. The set  corresponds to pairs that are achievable by some
corresponds to pairs that are achievable by some 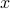 that is feasible for the original problem.
that is feasible for the original problem.
Dual function
The dual function is

In the scalar problem above, the dual function is easy to compute, either by a direct (brute force) scan of values in ![[-10,10]](eqs/7397884364733334519-130.png) , or by taking derivatives of the above objective function, and roots of a
, or by taking derivatives of the above objective function, and roots of a  -th order polynomial.
-th order polynomial.
The geometric interpretation of  is a follows. We have
is a follows. We have

Consider a non-vertical line in  plane, with non-positive slope given by
plane, with non-positive slope given by  . This line can be expressed as
. This line can be expressed as

where the value of the constant is the intercept, that is, the point on the line on the  -axis.
-axis.
Dual problem
The dual problem:

amounts to finding the best line, that is, search for slopes  that achieves the highest intercept. It corresponds to replacing
that achieves the highest intercept. It corresponds to replacing  with its convex hull.
with its convex hull.


 when
when  . The fatter part of the blue line (which is inside corresponds to the points
. The fatter part of the blue line (which is inside corresponds to the points  , in the smallest value of
, in the smallest value of 
 , where
, where  , for
, for 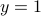 . The value of
. The value of  is corresponds to the line
is corresponds to the line  which has the smallest intercept
which has the smallest intercept  , and intersects the set
, and intersects the set  .
.
 intercepting
intercepting  , is that largest intercept; in our case, the optimal dual variable is
, is that largest intercept; in our case, the optimal dual variable is  . In this problem, there is a duality gap, in the sense that
. In this problem, there is a duality gap, in the sense that  . This is the case for most non-convex problems.
. This is the case for most non-convex problems.