Exercises
Matrix products
Let
 and
and  be two maps. Let
be two maps. Let  be the composite map
be the composite map  , with values
, with values  for
for 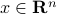 . Show that the derivatives of
. Show that the derivatives of  can be expressed via a matrix-matrix product, as
can be expressed via a matrix-matrix product, as  , where the Jacobian matrix of
, where the Jacobian matrix of  at
at 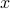 is defined as the matrix
is defined as the matrix  with
with  element
element  .
.
Special matrices
A matrix
 is a permutation matrix if it is a permutation of the columns of the
is a permutation matrix if it is a permutation of the columns of the  identity matrix.
identity matrix. For a
 matrix
matrix 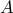 , we consider the products
, we consider the products  and
and  . Describe in simple terms what these matrices look like with respect to the original matrix
. Describe in simple terms what these matrices look like with respect to the original matrix 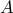 .
.Show that
 is orthogonal.
is orthogonal.Show that
 .
.
Linear maps, dynamical systems
Let
 be a linear map. Show how to compute the (unique) matrix
be a linear map. Show how to compute the (unique) matrix 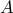 such that
such that  for every
for every 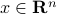 , in terms of the values of
, in terms of the values of  at appropriate vectors, which you will determine.
at appropriate vectors, which you will determine.Consider a discrete-time linear dynamical system (for background, see here) with state
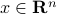 , input vector
, input vector  , and output vector
, and output vector  , that is described by the linear equations
, that is described by the linear equations

with  ,
,  , and
, and  given matrices.
given matrices.
-
Assuming that the system has initial condition
 , express the output vector at time
, express the output vector at time  as a linear function of
as a linear function of  ; that is, determine a matrix
; that is, determine a matrix  such that
such that  , where
, where  is a vector containing all the inputs up to and including at time
is a vector containing all the inputs up to and including at time  .
.What is the interpretation of the range of
 ?
?
Matrix inverses, norms
Show that a square matrix is invertible if and only if its determinant is non-zero. You can use the fact that the determinant of a product is a product of the determinant, together with the QR decomposition of the matrix
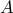 .
.Let
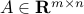 ,
,  , and let
, and let  . Show that
. Show that  where
where  denotes the largest singular value norm of its matrix argument.
denotes the largest singular value norm of its matrix argument.