Declarative Program Analysis and Optimization

ECTAs: Searching Entangled Program Spaces

• Wednesday, March 13, 2024
• Discussion lead: Altan, Tyler
• Reading guide due Monday, March 11 at 2:30pm
• Paper link

Suggested reading strategy

1. Read through the DFTA primer and From acceptance to enumeration background sections below.
2. Watch the ICFP’22 Searching Entangled Program Spaces talk at your preferred playback rate
3. Read sections in order: 1, 2, 6, 3.1-3.3, 7.
4. Sections 3.4, 3.5, and 4 can be hard to read because they get deep into the formalism. We summarize the key ideas below.
5. Section 5 describes their approach for cyclic ECTAs; feel free to read, but it isn’t too important and we summarize the idea below.

Section 3.4 summary

The union of two ECTAs is an ECTA that accepts a tree if either ECTA accepts. Because the root node of the ECTA node is a state node, and state nodes represent disjunction (the DFTA can take any transition to get to that state), the union of two ECTAs is just the union of transition nodes that point into the root state node.

Justification: if a tree $T$ was accepted by one of the original ECTAs, consider the last transition that ECTA took. That transition exists in the unioned ECTA by construction, so the unioned ECTA is also able to reach that transition on $T$ and accept.

The intersection of two ECTAs is more complicated. The intersection of two ECTAs $A$ and $B$ is an ECTA that accepts a tree if both original ETCAs accept. To motivate our construction of the intersection ECTA, suppose a tree $T$ was accepted on both original ETCAs. Then both ECTAs must have taken some final transition to accept $T$, so there must be some transition subtree $A’ \in A$ and $B’ \in B$ that both accepts $T$. Then, the ECTA $\mathbf{U}(A’ \sqcap B’)$ accepts $T$ (assuming inductively that intersection is correct). Hence, by considering all transition pairs $(A’, B’)$, taking their intersections, and adding them as children of union node, we can construct an ECTA that accepts if both $A$ and $B$ accept.

Justification: if both $A$ and $B$ accept on $T$, then their last transition must be some $A^*$ and $B^*$ respectively. Then the pair transition $A^* \sqcap B^*$ in the intersection ECTA also accepts on $T$, and so the overall intersection ECTA also accepts.

Section 3.5 summary

Using the intersection machinery defined above, we can formally define an algorithm to statically reduce an ECTA. At a high level, the algorithm is as follows:

• For every constraint set:
  • For every path $p$ in the constraint set:
    • Let $n|_p$ be the ECTA that is constructed by unioning of all ECTAs that are reachable from the root following the path $p$. Note that $n|_p$ may be large because disjunctions mean that a path may point to many sub-ECTAs.
    • Note that $n|_p$ represents all possible subexpressions for the path $p$ in the ECTA.
  • Apply the equality constraint: let $n^*$ be the intersection of all $n|_p$. The ECTA $n^*$ thus only represents subexpressions that are represented by every path in the constraint set.
  • “Push down” the equality constraint into the ECTA; for every path $p$ in the constraint set:
    • Intersect $n^*$ with every sub-ECTA that is reachable from the root following $p$. Again, disjunctions mean there may be many such ETCAs.

Section 4 summary

This section is pretty technical, so we summarize the high-level idea of dynamic reduction.

We would like to simply pick a transition at each state in a top-down manner. However, as the paper shows, this does not play well with the equality constraints, and leads to excessive enumeration of inconsistent terms. Instead, as we push equalities down through paths, we introduce placeholder variables to capture equalities that came from above (i.e. a higher “scope”). Eventually, the child subautomaton will become fully constrained to some placeholder variable: the path in the constraint becomes epsilon. At this point, we can hoist the subautomaton out of the partially enumerated term and replace it with the placeholder variable. Every time such a hoisting is done, we intersect the hoisted automaton with what has already been lifted out for that placeholder variable, if any. This repeated hoisting and intersecting is the core of the dynamic reduction.

Section 5 summary

The paper’s adapts their approach to cyclic ECTAs by restricting their algorithm to ECTAs that do not have equality constraints “inside” cyclic portions. Intuitively, this means that the cyclic portion of the DFTA can be “unrolled” statically many times so the “target” nodes of equality constraints are in acyclic portions of the (now unrolled) graph (“lasso form”). Then, the cyclic portions can be thought of leaf nodes containing “infinitely many” terms and can be ignored/intersected/unioned just like a normal DFTA (because they no longer participate in any equality constraints).

DFTA primer

The short story:

Deterministic finite state automata (DFA) decide whether a string is in a particular language.
Deterministic finite tree automata (DFTA) decide whether a tree is in a particular tree language.

The long story:

DFA review

At a high level, a DFA operates by ingesting symbols sequentially from an alphabet. For each symbol, the DFA transitions to another state based on the current state and the ingested symbol. Let $Q$ be the set of states and $\Sigma$ be the alphabet. The transition function $\delta$ for a DFA is a function $Q \times \Sigma \to Q$; i.e. given a current state and a symbol, it returns the next state.

For example, consider the DFA that accepts if there is an odd number of a’s in a string of a’s and b’s. The states are ${q_0, q_1}$, the accepting states are ${q_1}$, and the transition function is

One possible way to interpret the operation of a DFA is that it continually “reduces” the prefix of the string. On the input ‘aaabbab’, we can prepend the state to the string, and reduce the prefix:

Finally, when the input is exhausted, the DFA accepts if the final state is in an accepting state. $q_0$ is not an accepting state, so the DFA rejects this string.

DFTAs

DFTAs are a generalization of DFAs in the following manner: instead of the transition function $\delta$ being defined on a state and the next symbol, the transition function is defined on a tree vertex and its direct children. The operation of the DFTA “reduces” subtrees from bottom to top until the entire tree is reduced. If the final state is an accepting state, then the DFTA accepts.

For example, we can consider a DFTA that recognizes whether a boolean expression evaluates to True. Let $\Sigma = \{\And, \;\Or, \;\Not, \;\True, \;\False\}$ and $Q = \{q_T, q_F\}$. It is straightforward to derive the transition function $\delta$ from standard boolean logic:

The accepting states are $\{q_T\}$.

Because it is difficult to draw trees in MathJax, we show how this DFTA accepts a boolean expression written out instead. We reduce in order of deepest leaf, breaking ties left-to-right:

So the DFTA rejects since the state associated with the root is $q_F$.

Finally, while in the above reduction we removed intermediate states from the expression/tree, it is often customary to show the reduction process with a tree of intermediate states. In ASCII art:

                OR                                      qF
               /   \                                   /  \
              /     \                                 /    \
             /       \                               /      \
            /         \                             /        \
           AND        AND                          qF        qF
          /   \      /  \          reduces        /  \      /  \
         |     |    |    \        ========>      |    |    |    \
        NOT   NOT  TRUE  NOT                     qF   qF   qT   qF
               |          |                           |         |
               |          |                           |         |
              TRUE       NOT                          qT        qT
                          |                                     |
                          |                                     |
                        FALSE                                   qF

From acceptance to enumeration

Above, we constructed a DFTA that can accept whether a tree is in a given tree language. But for the paper, we want to do the reverse—we really want to enumerate all sentences in a tree language [that satisfy some equality constraints].

Indeed, for a cyclic DFTA, this is hard to do (one reason being that the language might be infinite) so instead we restrict this example to acyclic DFTAs.

The key observation that we can use for enumeration is that multiple transitions can produce the same state. For example, in the above boolean expression DFTA, there were many ways to produce $q_T$: a subset are $\Not\; q_F,\; q_T \;\And\; q_T,\; q_T \;\Or\;q_F$. That is, possibilities of reducing to a state represent disjunction. As long as any transition rule to $q_T$ is satisifed, one can produce $q_T$.

But, for example, in order to produce $q_T \;\Or\; q_F$, one must produce states $q_T$ and $q_F$ as children of an $\Or$ node. All three must be present for the reduction to $q_T$ to be allowed under this DFTA. That is, inputs to a transition rule represent conjunction.

So, to create a diagram to represent the enumeration of the tree language that is accepted by a DFTA, we can start at the accepting states (in this case just $q_T$) and make them the roots of the diagram. Then, consider all possible ways to reduce to $q_T$, and add them as nodes with edges to the root. For example, here is a diagram that represents all six boolean expression trees that evaluate to True of height 1 or less:

States in this diagram are represented by circular nodes, while transitions are represented by rectangular nodes. To enumerate expressions from this diagram, we must “pick” transitions for each state starting from the top and going down. Starting at the top, we see that in order to transition to state $q_{T0}$, we need to pick any of its children.

Suppose we pick the first $\Or$ node; then, in order to satisfy the requirements for this transition (its children), we need to pick some way to transition to $q_{T1}$ and another way to transition to $q_{F1}$. The only way to transition to these is picking the literals $\True$ and $\False$ respectively. So these choices enumerate exactly the boolean expression $\True \;\Or\; \False$. (Starting from the top is important because if we picked the $\True$ node to transition into $q_{T0}$, we would not have needed to pick variables for $q_{T1}$ or $q_{F1}$.)

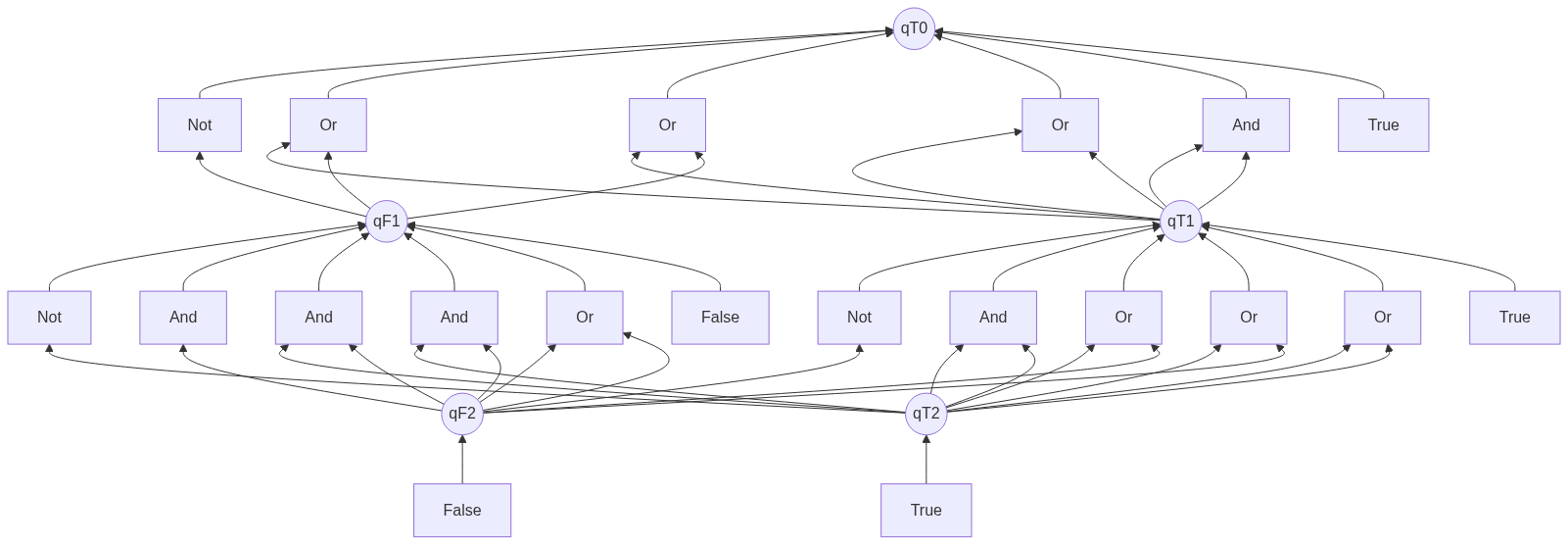
While the above diagram was not particularly concise, here is a diagram that represents all very many boolean expressions of height 2 or less:

Adding another layer to this diagram would only add another ~14 nodes, but would represent combinatorially many more terms, so in general such a diagram can represent combinatorially many expressions.

Discussion questions

1. In what ways is this work related to e-graphs/equality saturation?
2. This style of enumeration feels like querying a (compact) database… are database query optimization techniques relevant?

See also:

• Egraphs are DFTAs.
• Worst case optimal joins