Homework 4: Data Abstraction and Trees
Due by 11:59pm on Friday, 3/1
Instructions
Submission: When you are done, submit with python3 ok
--submit. You may submit more than once before the deadline; only the
final submission will be scored. Check that you have successfully submitted
your code on okpy.org. See Lab 0 for more instructions on
submitting assignments.
Using Ok: If you have any questions about using Ok, please refer to this guide.
Readings: You might find the following references useful:
Grading: Homework is graded based on effort, not correctness. However, there is no partial credit; you must show substantial effort on every problem to receive any points.
Required questions
Trees
Q1: Replace Leaf
Define replace_leaf, which takes a tree t, a value old, and a value new.
replace_leaf returns a new tree that's the same as t except that every leaf
value equal to old has been replaced with new.
def replace_leaf(t, old, new):
"""Returns a new tree where every leaf value equal to old has
been replaced with new.
>>> yggdrasil = tree('odin',
... [tree('balder',
... [tree('thor'),
... tree('loki')]),
... tree('frigg',
... [tree('thor')]),
... tree('thor',
... [tree('sif'),
... tree('thor')]),
... tree('thor')])
>>> laerad = copy_tree(yggdrasil) # copy yggdrasil for testing purposes
>>> print_tree(replace_leaf(yggdrasil, 'thor', 'freya'))
odin
balder
freya
loki
frigg
freya
thor
sif
freya
freya
>>> laerad == yggdrasil # Make sure original tree is unmodified
True
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q replace_leafQ2: Pruning Leaves
Define a function prune_leaves that given a tree t and a tuple of values
vals, produces a version of t with all its leaves that are in vals
removed. Do not attempt to try to remove non-leaf nodes and do not remove
leaves that do not match any of the items in vals. Return None if pruning
the tree results in there being no nodes left in the tree.
def prune_leaves(t, vals):
"""Return a modified copy of t with all leaves that have a label
that appears in vals removed. Return None if the entire tree is
pruned away.
>>> t = tree(2)
>>> print(prune_leaves(t, (1, 2)))
None
>>> numbers = tree(1, [tree(2), tree(3, [tree(4), tree(5)]), tree(6, [tree(7)])])
>>> print_tree(numbers)
1
2
3
4
5
6
7
>>> print_tree(prune_leaves(numbers, (3, 4, 6, 7)))
1
2
3
5
6
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q prune_leavesMobiles
Acknowledgements. This mobile example is based on a classic problem from Structure and Interpretation of Computer Programs, Section 2.2.2.
Hint: for more information on this problem (with more pictures!) please refer to this document
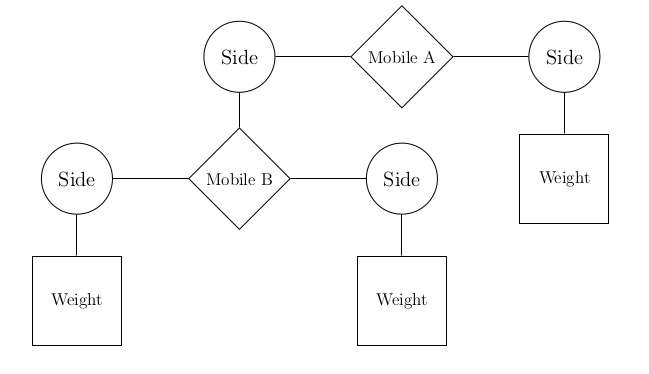
A mobile is a type of hanging sculpture. A binary mobile consists of two sides. Each side is a rod of a certain length, from which hangs either a weight or another mobile.
We will represent a binary mobile using the data abstractions below.
- A
mobilehas a leftsideand a rightside. - A
sidehas a positive length and something hanging at the end, either amobileorweight. - A
weighthas a positive size.
Q3: Weights
Implement the weight data abstraction by completing the weight constructor
and the size selector so that a weight is represented using a two-element list
where the first element is the string 'weight'. The total_weight example is
provided to demonstrate use of the mobile, side, and weight abstractions.
def mobile(left, right):
"""Construct a mobile from a left side and a right side."""
assert is_side(left), "left must be a side"
assert is_side(right), "right must be a side"
return ['mobile', left, right]
def is_mobile(m):
"""Return whether m is a mobile."""
return type(m) == list and len(m) == 3 and m[0] == 'mobile'
def left(m):
"""Select the left side of a mobile."""
assert is_mobile(m), "must call left on a mobile"
return m[1]
def right(m):
"""Select the right side of a mobile."""
assert is_mobile(m), "must call right on a mobile"
return m[2]def side(length, mobile_or_weight):
"""Construct a side: a length of rod with a mobile or weight at the end."""
assert is_mobile(mobile_or_weight) or is_weight(mobile_or_weight)
return ['side', length, mobile_or_weight]
def is_side(s):
"""Return whether s is a side."""
return type(s) == list and len(s) == 3 and s[0] == 'side'
def length(s):
"""Select the length of a side."""
assert is_side(s), "must call length on a side"
return s[1]
def end(s):
"""Select the mobile or weight hanging at the end of a side."""
assert is_side(s), "must call end on a side"
return s[2]def weight(size):
"""Construct a weight of some size."""
assert size > 0
"*** YOUR CODE HERE ***"
def size(w):
"""Select the size of a weight."""
assert is_weight(w), 'must call size on a weight'
"*** YOUR CODE HERE ***"
def is_weight(w):
"""Whether w is a weight."""
return type(w) == list and len(w) == 2 and w[0] == 'weight'Use Ok to test your code:
python3 ok -q total_weightQ4: Balanced
Hint: for more information on this problem (with more pictures!) please refer to this document
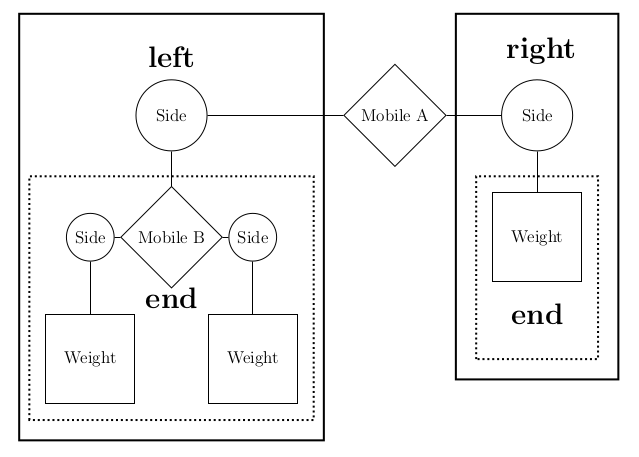
Implement the balanced function, which returns whether m is a balanced
mobile. A mobile is balanced if two conditions are met:
- The torque applied by its left side is equal to that applied by its right side. Torque of the left side is the length of the left rod multiplied by the total weight hanging from that rod. Likewise for the right.
- Each of the mobiles hanging at the end of its sides is balanced.
Hint: You may find it helpful to assume that weights themselves are balanced.
def balanced(m):
"""Return whether m is balanced.
>>> t, u, v = examples()
>>> balanced(t)
True
>>> balanced(v)
True
>>> w = mobile(side(3, t), side(2, u))
>>> balanced(w)
False
>>> balanced(mobile(side(1, v), side(1, w)))
False
>>> balanced(mobile(side(1, w), side(1, v)))
False
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q balancedQ5: Totals
Implement totals_tree, which takes a mobile (or weight) and returns a
tree whose root is its total weight and whose branches are trees for the ends
of the sides.
def totals_tree(m):
"""Return a tree representing the mobile with its total weight at the root.
>>> t, u, v = examples()
>>> print_tree(totals_tree(t))
3
2
1
>>> print_tree(totals_tree(u))
6
1
5
3
2
>>> print_tree(totals_tree(v))
9
3
2
1
6
1
5
3
2
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q totals_treeJust for fun Question
This question is out of scope for 61a. Do it if you want an extra challenge!
Q6: Church numerals
The logician Alonzo Church invented a system of representing non-negative integers entirely using functions. The purpose was to show that functions are sufficient to describe all of number theory: if we have functions, we do not need to assume that numbers exist, but instead we can invent them.
Your goal in this problem is to rediscover this representation known as Church
numerals. Here are the definitions of zero, as well as a function that
returns one more than its argument:
def zero(f):
return lambda x: x
def successor(n):
return lambda f: lambda x: f(n(f)(x))First, define functions one and two such that they have the same behavior
as successor(zero) and successsor(successor(zero)) respectively, but do
not call successor in your implementation.
Next, implement a function church_to_int that converts a church numeral
argument to a regular Python integer.
Finally, implement functions add_church, mul_church, and pow_church that
perform addition, multiplication, and exponentiation on church numerals.
def one(f):
"""Church numeral 1: same as successor(zero)"""
"*** YOUR CODE HERE ***"
def two(f):
"""Church numeral 2: same as successor(successor(zero))"""
"*** YOUR CODE HERE ***"
three = successor(two)
def church_to_int(n):
"""Convert the Church numeral n to a Python integer.
>>> church_to_int(zero)
0
>>> church_to_int(one)
1
>>> church_to_int(two)
2
>>> church_to_int(three)
3
"""
"*** YOUR CODE HERE ***"
def add_church(m, n):
"""Return the Church numeral for m + n, for Church numerals m and n.
>>> church_to_int(add_church(two, three))
5
"""
"*** YOUR CODE HERE ***"
def mul_church(m, n):
"""Return the Church numeral for m * n, for Church numerals m and n.
>>> four = successor(three)
>>> church_to_int(mul_church(two, three))
6
>>> church_to_int(mul_church(three, four))
12
"""
"*** YOUR CODE HERE ***"
def pow_church(m, n):
"""Return the Church numeral m ** n, for Church numerals m and n.
>>> church_to_int(pow_church(two, three))
8
>>> church_to_int(pow_church(three, two))
9
"""
"*** YOUR CODE HERE ***"
Use Ok to test your code:
python3 ok -q church_to_int
python3 ok -q add_church
python3 ok -q mul_church
python3 ok -q pow_church