Lab 09: Scheme
Due at 11:59pm on Friday, 4/5/2019.
Starter Files
Download lab09.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the Ok autograder.
Submission
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
Check that you have successfully submitted your code on
okpy.org.
- To receive credit for this lab, you must complete Questions 2 through 5 in lab09.scm and submit through Ok.
- Questions 6 through 11 are extra practice. They can be found in the lab09_extra.scm file. It is recommended that you complete these problems on your own time.
Topics
Note: We're diving into a new programming language today! As such, the Topics section is lengthier than usual and covers a lot of fundamentals that will help you build a good foundation for understanding the Scheme material in this course. Make sure you are familiar with all the features of Scheme described in this section.
Scheme
Scheme is a famous functional programming language from the 1970s. It is a dialect of Lisp (which stands for LISt Processing). The first observation most people make is the unique syntax, which uses a prefix notation and (often many) nested parentheses (see http://xkcd.com/297/). Scheme features first-class functions and optimized tail-recursion, which were relatively new features at the time.
Our course uses a custom version of Scheme (which you will build for Project 4) included in the starter ZIP archive. To start the interpreter, type
python3 scheme. To run a Scheme program interactively, typepython3 scheme -i <file.scm>. To exit the Scheme interpreter, type(exit).
You may find it useful to try scheme.cs61a.org when working through problems, as it can draw environment and box-and-pointer diagrams and it lets you walk your code step-by-step (similar to Python Tutor). Don't forget to submit your code through Ok though!
Expressions
Atomic Expressions
Just like in Python, atomic, or primitive, expressions in Scheme take a single step to evaluate. These include numbers, booleans, symbols.
scm> 1234 ; integer
1234
scm> 123.4 ; real number
123.4Symbols
Out of these, the symbol type is the only one we didn't encounter in Python. A symbol acts a lot like a Python name, but not exactly. Specifically, a symbol in Scheme is also a type of value. On the other hand, in Python, names only serve as expressions; a Python expression can never evaluate to a name.
scm> quotient ; A name bound to a built-in procedure
#[quotient]
scm> 'quotient ; An expression that evaluates to a symbol
quotient
scm> 'hello-world!
hello-world!Booleans
In Scheme, all values except the special boolean value #f are interpreted
as true values (unlike Python, where there are some false-y values like 0).
Our particular version of the Scheme interpreter allows you to write True and
False in place of #t and #f. This is not standard.
scm> #t
#t
scm> #f
#fCall expressions
Like Python, the operator in a Scheme call expression comes before all the operands. Unlike Python, the operator is included within the parentheses and the operands are separated by spaces rather than with commas. However, evaluation of a Scheme call expression follows the exact same rules as in Python:
- Evaluate the operator. It should evaluate to a procedure.
- Evaluate the operands, left to right.
- Apply the procedure to the evaluated operands.
Here are some examples using built-in procedures:
scm> (+ 1 2)
3
scm> (- 10 (/ 6 2))
7
scm> (modulo 35 4)
3
scm> (even? (quotient 45 2))
#tSpecial forms
The operator of a special form expression is a special form. What makes a special form "special" is that they do not follow the three rules of evaluation stated in the previous section. Instead, each special form follows its own special rules for execution, such as short-circuiting before evaluating all the operands.
Some examples of special forms that we'll study today are the if, cond,
define, and lambda forms. Read their corresponding sections below to find
out what their rules of evaluation are!
Control Structures
if Expressions
The if special form allows us to evaluate one of two expressions based on a
predicate. It takes in two required arguments and an optional third argument:
(if <predicate> <if-true> [if-false])The first operand is what's known as a predicate expression in Scheme, an
expression whose value is interpreted as either #t or #f.
The rules for evaluating an if special form expression are as follows:
- Evaluate
<predicate>. - If
<predicate>evaluates to a truth-y value, evaluate and return the value if the expression<if-true>. Otherwise, evaluate and return the value of[if-false]if it is provided.
Can you see why this expression is a special form? Compare the rules between a
regular call expression and an if expression. What is the difference?
Step 2 of evaluating call expressions requires evaluating all of the operands in order. However, an
ifexpression will only evaluate two of its operands, the conditional expression and either<true-result>or<false-result>. Because we don't evaluate all the operands in anifexpression, it is a special form.
Let's compare a Scheme if expression with a Python if statement:
| Scheme | Python |
|---|---|
|
|
Although the code may look the same, what happens when each block of code is
evaluated is actually very different. Specifically, the Scheme expression,
given that it is an expression, evaluates to some value. However, the Python
if statement simply directs the flow of the program.
Another difference between the two is that it's possible to add more lines of
code into the suites of the Python if statement, while a Scheme if
expression expects just a single expression for each of the true result and the
false result.
One final difference is that in Scheme, you cannot write elif cases. If you
want to have multiple cases using the if expression, you would need multiple
branched if expressions:
| Scheme | Python |
|---|---|
|
|
cond Expressions
Using nested if expressions doesn't seem like a very practical way to take
care of multiple cases. Instead, we can use the cond special form, a general
conditional expression similar to a multi-clause if/elif/else conditional
expression in Python. cond takes in an arbitrary number of arguments known as
clauses. A clause is written as a list containing two expressions: (<p>
<e>).
(cond
(<p1> <e1>)
(<p2> <e2>)
...
(<pn> <en>)
[(else <else-expression>)])The first expression in each clause is a predicate. The second expression in
the clause is the return expression corresponding to its predicate. The
optional else clause has no predicate.
The rules of evaluation are as follows:
- Evaluate the predicates
<p1>,<p2>, ...,<pn>in order until you reach one that evaluates to a truth-y value. - If you reach a predicate that evaluates to a truth-y value, evaluate and return the corresponding expression in the clause.
- If none of the predicates are truth-y and there is an
elseclause, evaluate and return<else-expression>.
As you can see, cond is a special form because it does not evaluate its
operands in their entirety; the predicates are evaluated separately from their
corresponding return expression. In addition, the expression short circuits
upon reaching the first predicate that evaluates to a truth-y value, leaving
the remaining predicates unevaluated.
The following code is roughly equivalent (see the explanation in the if expression section):
| Scheme | Python |
|---|---|
|
|
Lists
As you read through this section, it may be difficult to understand the differences between the various representations of Scheme containers. We recommend that you use our online Scheme interpreter to see the box-and-pointer diagrams of pairs and lists that you're having a hard time visualizing! (Use the command
(autodraw)to toggle the automatic drawing of diagrams.)
Lists
Scheme lists are very similar to the linked lists we've been working with in
Python. Just like how a linked list is constructed of a series of Link
objects, a Scheme list is constructed with a series of pairs, which are created
with the constructor cons.
Scheme lists require that the cdr is either another list or nil, an empty list.
A list is displayed in the interpreter as a sequence of values (similar to the
__str__ representation of a Link object). For example,
scm> (cons 1 (cons 2 (cons 3 nil)))
(1 2 3)Here, we've ensured that the second argument of each cons expression is
another cons expression or nil.

We can retrieve values from our list with the car and cdr procedures, which
now work similarly to the Python Link's first and rest attributes.
(Curious about where these weird names come from? Check out their
etymology.)
scm> (define a (cons 1 (cons 2 (cons 3 nil)))) ; Assign the list to the name a
scm> a
(1 2 3)
scm> (car a)
1
scm> (cdr a)
(2 3)
scm> (car (cdr (cdr a)))
3If you do not pass in a pair or nil as the second argument to cons, it will
error:
scm> (cons 1 2)
Errorlist Procedure
There are a few other ways to create lists. The list procedure takes in an
arbitrary number of arguments and constructs a list with the values of these
arguments:
scm> (list 1 2 3)
(1 2 3)
scm> (list 1 (list 2 3) 4)
(1 (2 3) 4)
scm> (list (cons 1 (cons 2 nil)) 3 4)
((1 2) 3 4)Note that all of the operands in this expression are evaluated before being put into the resulting list.
Quote Form
We can also use the quote form to create a list, which will construct the exact
list that is given. Unlike with the list procedure, the argument to ' is
not evaluated.
scm> '(1 2 3)
(1 2 3)
scm> '(cons 1 2) ; Argument to quote is not evaluated
(cons 1 2)
scm> '(1 (2 3 4))
(1 (2 3 4))Built-In Procedures for Lists
There are a few other built-in procedures in Scheme that are used for lists. Try them out in the interpreter!
scm> (null? nil) ; Checks if a value is the empty list
______True
scm> (append '(1 2 3) '(4 5 6)) ; Concatenates two lists
______(1 2 3 4 5 6)
scm> (length '(1 2 3 4 5)) ; Returns the number of elements in a list
______5Lambdas
lambda special form:
(lambda (<param1> <param2> ...) <body>)This expression will create and return a function with the given parameters and
body, but it will not alter the current environment. This is very similar to a
lambda expression in Python!
scm> (lambda (x y) (+ x y)) ; Returns a lambda function, but doesn't assign it to a name
(lambda (x y) (+ x y))
scm> ((lambda (x y) (+ x y)) 3 4) ; Create and call a lambda function in one line
7A procedure may take in any number of parameters. The <body> may contain
multiple expressions. There is not an equivalent version of a Python return
statement in Scheme. The function will simply return the value of the last
expression in the body.
Defining procedures
define is used to define variables and functions in Scheme.
There are two versions of the define special form. To define variables, we
use the define form with the following syntax:
(define <name> <expression>)The rules to evaluate this expression are
- Evaluate the
<expression>. - Bind its value to the
<name>in the current frame. - Return
<name>.
The second version of define is used to define procedures:
(define (<name> <param1> <param2> ...) <body> )To evaluate this expression:
- Create a lambda procedure with the given parameters and
<body>. - Bind the procedure to the
<name>in the current frame. - Return
<name>.
The following two expressions are equivalent:
scm> (define foo (lambda (x y) (+ x y)))
foo
scm> (define (foo x y) (+ x y))
foodefine is a special form because its operands are not evaluated at all! For
example, <body> is not evaluated when a procedure is defined, but rather when
it is called. <name> and the parameter names are all names that should not be
evaluated when executing this define expression.
Checkoff 5
Q1: Exam Check-In
Check in with an academic intern or TA about how you did on the exam, what you did right when preparing for this exam, what you plan to do better next time, etc.
Required Questions
What Would Scheme Display?
Q2: WWSD: Lists
Use Ok to test your knowledge with the following "What Would Scheme Display?" questions:
python3 ok -q wwsd-lists -u
scm> (cons 1 (cons 2 nil))
______(1 2)
scm> (car (cons 1 (cons 2 nil)))
______1
scm> (cdr (cons 1 (cons 2 nil)))
______(2)
scm> (list 1 2 3)
______(1 2 3)
scm> '(1 2 3)
______(1 2 3)
scm> (cons 1 '(list 2 3)) ; Recall quoting
______(1 list 2 3)scm> '(cons 4 (cons (cons 6 8) ()))
______(cons 4 (cons (cons 6 8) ()))Coding Questions
Q3: Over or Under
Define a procedure over-or-under which takes in a number x and a number y
and returns the following:
- -1 if
xis less thany - 0 if
xis equal toy - 1 if
xis greater thany
(define (over-or-under x y)
'YOUR-CODE-HERE
(cond
((< x y) -1)
((= x y) 0)
(else 1))
Video walkthrough: https://youtu.be/UJ37SCaM3cQ?t=35m46s)
;;; Tests
(over-or-under 1 2)
; expect -1
(over-or-under 2 1)
; expect 1
(over-or-under 1 1)
; expect 0Use Ok to unlock and test your code:
python3 ok -q over-or-under -u
python3 ok -q over-or-underQ4: Filter
Write a procedure filter-lst, which takes a predicate f and a list lst, and
returns a new list containing only elements of the list that satisfy the
predicate. The output should contain the elements in the same order that they
appeared in the original list.
(define (filter-lst f lst)
'YOUR-CODE-HERE
(cond ((null? lst) '())
((f (car lst)) (cons (car lst) (filter-lst f (cdr lst))))
(else (filter-lst f (cdr lst))))
Video walkthrough: https://youtu.be/UJ37SCaM3cQ?t=39m39s)
;;; Tests
(define (even? x)
(= (modulo x 2) 0))
(filter-lst even? '(0 1 1 2 3 5 8))
; expect (0 2 8)Use Ok to unlock and test your code:
python3 ok -q filter-lst -u
python3 ok -q filter-lstQ5: Make Adder
Write the procedure make-adder which takes in an initial number,
num, and then returns a procedure. This returned procedure takes in a
number x and returns the result of x + num.
(define (make-adder num)
'YOUR-CODE-HERE
(lambda (x) (+ x num))
Video walkthrough: https://youtu.be/UJ37SCaM3cQ?t=47m4s)
;;; Tests
(define adder (make-adder 5))
(adder 8)
; expect 13Use Ok to unlock and test your code:
python3 ok -q make-adder -u
python3 ok -q make-adderOptional Questions
The following questions are for extra practice -- they can be found in the the lab09_extra.scm file. It is recommended that you complete these problems on your own time.
Q6: Make a List
Create the list with the following box-and-pointer diagram:
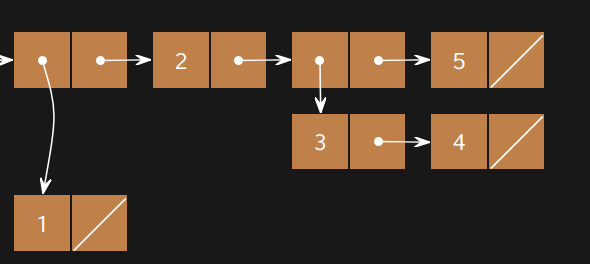
(define lst
'YOUR-CODE-HERE
(cons (cons 1 nil)
(cons 2
(cons (cons 3 (cons 4 nil))
(cons 5 nil)))))Use Ok to unlock and test your code:
python3 ok -q make-list -u
python3 ok -q make-listQ7: Compose
Write the procedure composed, which takes in procedures f and g
and outputs a new procedure. This new procedure takes in a number x
and outputs the result of calling f on g of x.
(define (composed f g)
'YOUR-CODE-HERE
(lambda (x) (f (g x))))Use Ok to unlock and test your code:
python3 ok -q composed -u
python3 ok -q composedQ8: Remove
Implement a procedure remove that takes in a list and returns a new list with
all instances of item removed from lst. You may assume the list will only
consist of numbers and will not have nested lists.
Hint: You might find the filter procedure useful.
(define (remove item lst)
'YOUR-CODE-HERE
(cond ((null? lst) '())
((equal? item (car lst)) (remove item (cdr lst)))
(else (cons (car lst) (remove item (cdr lst))))))
(define (remove item lst)
(filter (lambda (x) (not (= x item))) lst))
;;; Tests
(remove 3 nil)
; expect ()
(remove 3 '(1 3 5))
; expect (1 5)
(remove 5 '(5 3 5 5 1 4 5 4))
; expect (3 1 4 4)Use Ok to unlock and test your code:
python3 ok -q remove -u
python3 ok -q removeQ9: No Repeats
Implement no-repeats, which takes a list of numbers s as input and returns
a list that has all of the unique elements of s in the order that they first
appear, but no repeats. For example, (no-repeats (list 5 4 5 4 2 2))
evaluates to (5 4 2).
Hints: To test if two numbers are equal, use the = procedure. To test if
two numbers are not equal, use the not procedure in combination with =.
You may find it helpful to use the filter procedure.
(define (no-repeats s)
'YOUR-CODE-HERE
(if (null? s) s
(cons (car s)
(no-repeats (filter (lambda (x) (not (= (car s) x))) (cdr s))))))Use Ok to unlock and test your code:
python3 ok -q no-repeats -u
python3 ok -q no-repeatsQ10: Substitute
Write a procedure substitute that takes three arguments: a list s, an old
word, and a new word. It returns a list with the elements of s, but with
every occurrence of old replaced by new, even within sub-lists.
Hint: The built-in pair? predicate returns True if its argument is a cons
pair.
Hint: The = operator will only let you compare numbers, but using equal?
or eq? will let you compare symbols as well as numbers. For more information,
check out the Scheme Built-in Procedure Reference.
Use Ok to unlock and test your code:
python3 ok -q substitute -u
python3 ok -q substitute(define (substitute s old new)
'YOUR-CODE-HERE
(cond ((null? s) nil)
((pair? (car s)) (cons (substitute (car s) old new)
(substitute (cdr s) old new)))
((equal? (car s) old) (cons new
(substitute (cdr s) old new)))
(else (cons (car s) (substitute (cdr s) old new)))))Remember that we want to use equal? to compare symbols since = will only
work for numbers!
If the input list is empty, there's nothing to substitute. That's a pretty straightforward base case. Otherwise, our list has at least one item.
We can break the rest of this problem into roughly two big cases:
Nested list here
This means that (car s) is a pair. In this case, we have
to dig deeper and recurse on (car s) since there could be symbols to replace
in there. We must recurse on (cdr s) as well to handle the rest of the list.
No nested list here
This is the case if (car s) is not a pair. Of course, there could still be
nesting later on in the list, but we'll rely on our recursive call to handle
that.
If (car s) matches old, we'll make sure to use new in its place.
Otherwise, we'll use (car s) without replacing it. In both cases, we must
recurse on the rest of the list.
Video walkthrough: https://youtu.be/LAr-_twxXao
Q11: Sub All
Write sub-all, which takes a list s, a list of old words, and a
list of new words; the last two lists must be the same length. It returns a
list with the elements of s, but with each word that occurs in the second
argument replaced by the corresponding word of the third argument. You may use
substitute in your solution. Assume that olds and news have no elements
in common.
(define (sub-all s olds news)
'YOUR-CODE-HERE
(if (null? olds)
s
(sub-all (substitute s (car olds) (car news))
(cdr olds)
(cdr news))))Solving sub-all means just repeatedly doing the substitute operation we wrote
earlier. If this were Python, we might iterate over the list of olds and news,
calling substitute and saving the result for the next call. For example, it
might look something like this:
def sub_all(s, olds, news):
for o, n in zip(olds, news):
s = substitute(s, o, n)
return sIf that approach makes sense, then the only tricky part now is to translate that
logic into Scheme. Since we don't have access to iteration, we have to reflect
our progress in our recursive call to sub-all. This means shortening the list
of olds and news, and most importantly, feeding the result of substitute
into the next call.
Therefore, the base case is if we have nothing we want to replace in olds.
Checking if news is empty would also be ok, since olds and news should be
the same length.
What doesn't work, however, is checking if s is an empty list. While this
won't make your solution wrong on its own, it's an insufficient base case.
Remember that we're passing in s with elements replaced into the recursive
call, which means it won't become any shorter.
Video walkthrough: https://youtu.be/avYPLlaBtj0
Use Ok to unlock and test your code:
python3 ok -q sub-all -u
python3 ok -q sub-all