EECS20: Introduction to Real-Time Digital Systems
Lab02: Sampling and Aliasing
EECS20: Introduction to Real-Time Digital Systems
©1996 Regents of the University of California.
By K. H. Chiang, William T. Huang, Brian L. Evans.
URL: http://www-inst.eecs.berkeley.edu/~ee20
News: ucb.class.ee20
In lecture, we saw that a signal could be thought of as a measurement of some physical phenomenon. For example, a microphone changes a sound signal to an electrical signal by converting the variations in the pressure of the air to variations in the voltage on a conducting wire. Both the sound and electrical signals continuously vary with time and are called analog signals. In order to represent an analog signal on a digital computer, we approximate the analog signal by taking a finite number of samples [sampling] and then assigning a value to each sample [quantization]. In this laboratory, we will investigate sampling and aliasing in the context of tones.
We have all seen signals in various guises:
A one-dimensional signal is a function of a single variable. This variable is usually time, as it is in the four examples above. It need not be time, however; in image processing, the index variable is spatial- that is, we could be examining at intensity on a two-dimensional image as a function of where we're currently looking. For now though, let's stick with time as the index variable.
For the purposes of this course, we will be largely dealing with discrete time (DT) signals. DT signals are defined for a subset of points in time; usually this subset contains points evenly spaced in time. Examples of DT signals include:
In contrast to a DT signal, a continuous time (CT) signal is defined for
all points in time. However, when we try to represent a CT signal in a
computer, we run into a problem: we can assign a given signal a value at
any point in time, but where should we choose the next point in time in
relation to the current one? Between any two points in time, there are an
infinite number of points. So in a digital computer we represent signals as
discrete-time signals.![]()
What are the differences between CT and DT signals? A fundamental
difference is what happens to sinusoids. Consider a CT sine wave 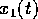 with frequency
with frequency 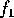 :
:

Now consider a DT signal which is the sampled version of the CT sine wave.
What does it mean to sample a CT signal? It means that at evenly spaced
points in time, we can think of closing a switch and recording the value of
the signal at those points in time. If the sampling period [the time
between successive samples] is 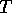 , then we have a new signal:
, then we have a new signal:
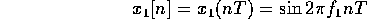
Note the change of variable from 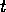 to
to  . If we sample with, say,
. If we sample with, say,
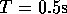 , the value of the signal at
, the value of the signal at 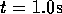 would be the same
as the value of the signal at
would be the same
as the value of the signal at 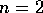 . Note also that
. Note also that  is an integer.
is an integer.
If the sampling period is 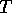 , the sampling frequency
, the sampling frequency 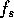 is then
is then
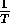 .
.
Why would one want to bother with sampling a sinusoid in the first place though? The key fact is this: sound is pressure variation. One of the most basic sounds, a pure tone, is generated through a sinusoidal variation in pressure.
What are the differences between CT and DT signals? A fundamental
difference is what happens to sinusoids. Consider a CT sine wave 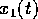 with frequency
with frequency 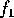 :
:

Now consider a CT sine wave 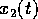 with frequency
with frequency 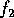 :
:

If 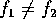 , it's obvious that the two sinusoids are different. How dull
and boring.
, it's obvious that the two sinusoids are different. How dull
and boring.
Let's take a look at DT. In particular, let's choose the frequencies such that
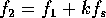 , where
, where 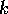 is an integer.
is an integer. 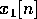 is:
is:
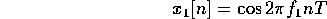
What about 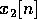 ?
?
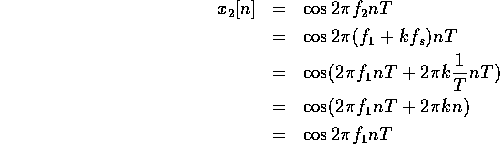
Notice that you can't tell the difference between 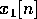 and
and 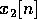 . This
effect- when the sampled versions of two different CT signals look the
same- is called aliasing. Note that the frequencies which get aliased
are dependent on the sampling period.
. This
effect- when the sampled versions of two different CT signals look the
same- is called aliasing. Note that the frequencies which get aliased
are dependent on the sampling period.
For example, consider a 1 Hz sine wave sampled with a sampling frequency
of 8 Hz, as in Figure 1; the points at which the sine is
sampled are indicated as circles. As predicted by our formula
[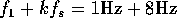 for
for 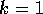 ], a 9 Hz sine wave passes through
those exact same points.
], a 9 Hz sine wave passes through
those exact same points.
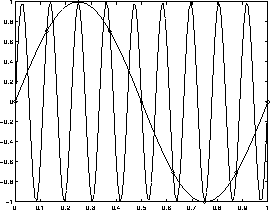
Figure 1: A 1 Hz sine wave sampled at 8 Hz looks like a 9 Hz sine
wave. The circles indicate where the samples are taken.
Another way to see aliasing is to sample a high frequency sinusoid at a rate which is too low to capture all the information in the CT signal.
It turns out that if you sample at a rate which is greater than twice the highest frequency in your CT signal, the frequency of the resulting DT signal will not alias to some other frequency. In other words:

The quantity 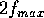 is referred to as the Nyquist rate.
is referred to as the Nyquist rate.
sound
saxis
sound command that takes a second
parameter- the sampling frequency. Experiment with various values of this
parameter. If you are using an HP, the sampling frequency is fixed to 8 kHz;
you should go to the lab and play around with the PCs instead for this part.
sound
command. Vary the frequency of the sinusoid and the sampling period. Caution:
if you set the frequency too low, you may potentially damage the speakers.
[Why?]
sound command; check the saxis command to disable/reenable the
autoscaling]. How can you make a sinusoid sound twice as loud? Can you hear
the effect of varying phase?
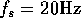 . Generate some
other sinusoids that alias to this 5 Hz sine wave.
. Generate some
other sinusoids that alias to this 5 Hz sine wave.
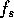 equal to 2.5 Hz, 5 Hz, 10 Hz,
and 20 Hz. Determine the Nyquist rate. Determine if aliasing has occurred in
your sampled signal, and what those aliased frequencies are. Is sampling
directly at the Nyquist rate a useful operation?
equal to 2.5 Hz, 5 Hz, 10 Hz,
and 20 Hz. Determine the Nyquist rate. Determine if aliasing has occurred in
your sampled signal, and what those aliased frequencies are. Is sampling
directly at the Nyquist rate a useful operation?
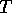 , relate a given discrete-time frequency to the
corresponding continuous-time frequency.
, relate a given discrete-time frequency to the
corresponding continuous-time frequency.