Gradient of a function
The gradient of a differentiable function 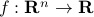 contains the first derivatives of the function with respect to each variable. As seen here, the gradient is useful to find the linear approximation of the function near a point.
contains the first derivatives of the function with respect to each variable. As seen here, the gradient is useful to find the linear approximation of the function near a point.
Definition
Composition rule
Examples
Geometric interpretation
Definition
The gradient of  at
at 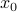 , denoted
, denoted 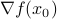 , is the vector in
, is the vector in 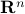 given by
given by

Examples:
Distance function: The distance function from a point
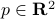 to another point
to another point 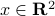 is defined as
is defined as
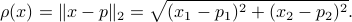
The function is differentiable, provided 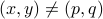 , which we assume. Then
, which we assume. Then
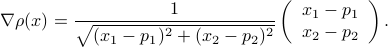
Log-sum-exp function: Consider the ‘‘log-sum-exp’’ function
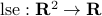 , with values
, with values
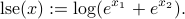
The gradient of 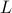 at
at  is
is
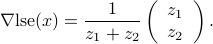
where 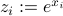 ,
, 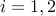 . More generally, the gradient of the function
. More generally, the gradient of the function 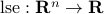 with values
with values
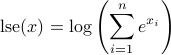
is given by
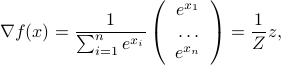
where 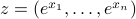 , and
, and 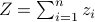 .
.
Composition rule with an affine function
If 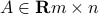 is a matrix, and
is a matrix, and 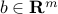 is a vector, the function
is a vector, the function 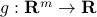 with values
with values

is called the composition of the affine map 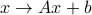 with
with  . Its gradient is given by (see here for a proof)
. Its gradient is given by (see here for a proof)
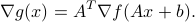
Geometric interpretation
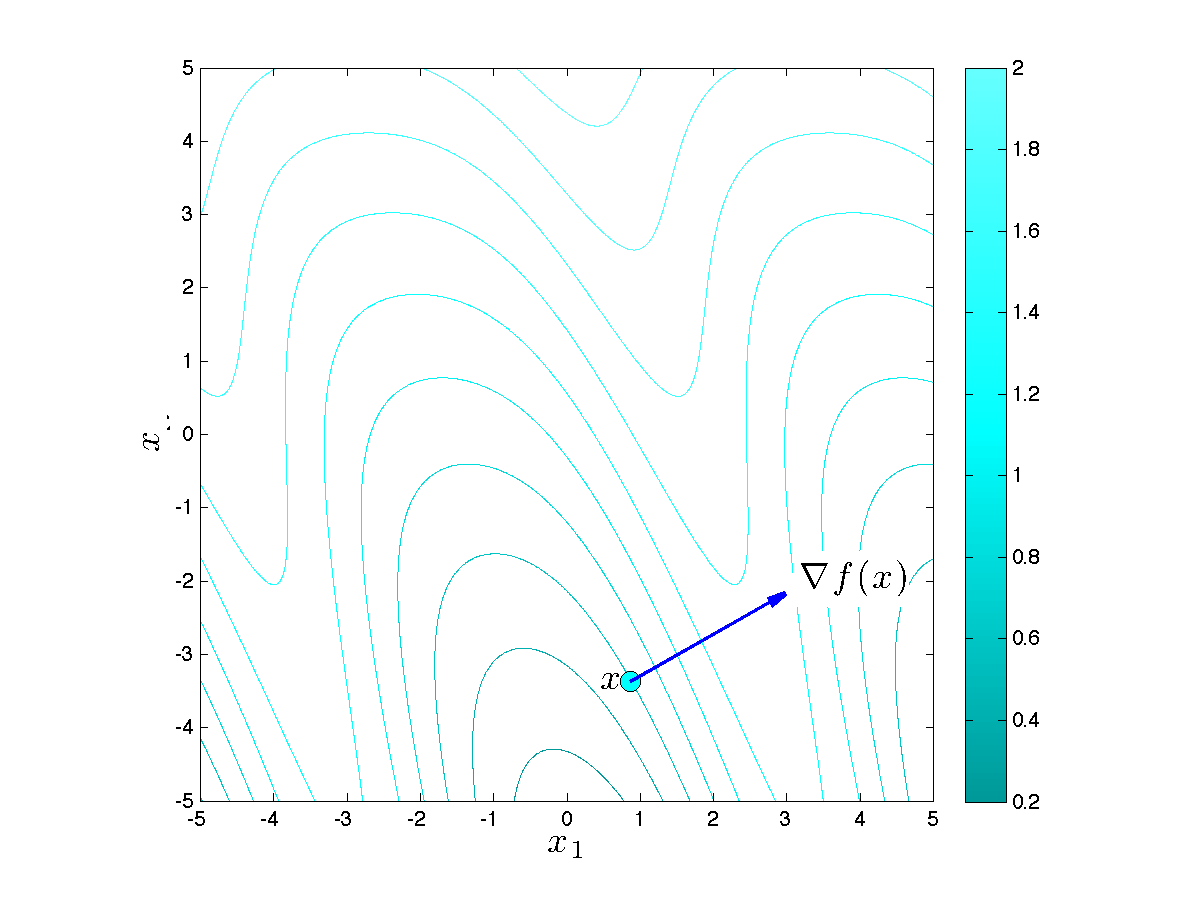
Geometrically, the gradient can be read on the plot of the level set of the function. Specifically, at any point  , the gradient is perpendicular to the level set, and points outwards from the sub-level set (that is, it points towards higher values of the function).
, the gradient is perpendicular to the level set, and points outwards from the sub-level set (that is, it points towards higher values of the function).
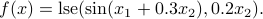
 .)
.)