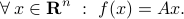Linear maps: equivalent definitions

Here are some equivalent definitions of linear functions.

A function 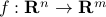$f : mathbf{R}^n rightarrow mathbf{R}^m$ is linear if and only if either one of the following conditions hold.

preserves scaling and addition of its arguments:
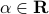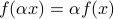- for every $x in mathbf{R}^n$ , and , ; and
- for every $x_1,x_2 in mathbf{R}^n$ , .

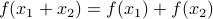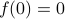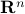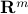vanishes at the origin: , and transforms any line segment in $mathbf{R}^n$ into another segment in $mathbf{R}^m$ :

$forall : x, y in mathbf{R}^n, ;; forall : lambda in [0,1] ~:~ f(lambda x + (1-lambda) y) = lambda f(x) + (1-lambda) f(y).$

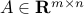is differentiable, vanishes at the origin, and the matrix of its derivatives is constant: there exist $A in mathbf{R}^{m times n}$ such that

$forall : x in mathbf{R}^n ~:~ f(x) = Ax .$