Log-Sum-Exp (LSE) Function and Properties

The log-sum-exp (LSE) function in \(\mathbf{R}^n\) is the function \(f : \mathbf{R}^n \rightarrow \mathbf{R}\), with domain the whole space \(\mathbf{R}^n\), and value at a point \(x \in \mathbf{R}^n\) given by

\[ f(x) = \log \left( \sum_{i=1}^n e^{x_i} \right) . \]

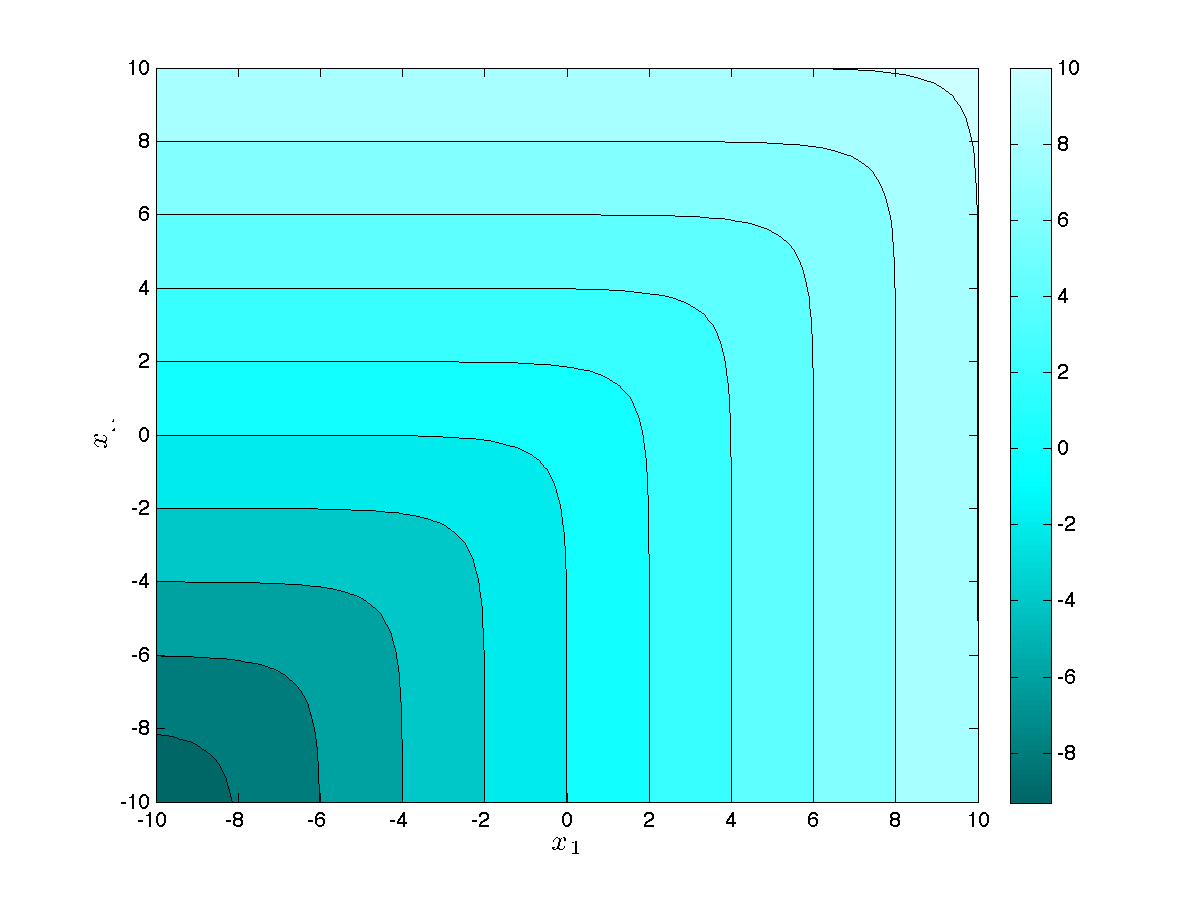The log-sum-exp function in \(\mathbf{R}^2\). For large positive values, the function is a smooth approximation to the maximum function \((x_1,x_2) \rightarrow \max(x_1,x_2)\).

The log-sum-exp function is increasing with respect to each argument, and convex.

Proof: The monotonicity of the log-sum-exp function is obvious. The convexity is obtained as follows. As seen here, the Hessian of the log-sum-exp function is

\[ \nabla^2 f(x) = \frac{1}{S(x)^2} \left( S(x) \mbox{\bf diag}(s(x))-s(x)s(x)^T \right), \]

where \(s(x) = (e^{x_1}, \ldots, e^{x_n})\), and \(S(x) = \sum_{i=1}^n s_i(x)\).

We need to check that for every \(z \in \mathbf{R}^n\), we have \(z^T \nabla^2 f(x)z \ge 0\). Let us fix a vector \(z\in \mathbf{R}^n\). We have

\[ \begin{array}{rcl} S(x)^2 \cdot z^T\nabla^2 f(x) z &=& z^T \left( S(x) \mbox{\bf diag}(s(x))-s(x)s(x)^T \right) z \\&=&\left( \sum_{i=1}^n s_i(x) z_i^2 \right) \left( \sum_{i=1}^n s_i(x) \right) - \left( \sum_{i=1}^n s_i(x) z_i \right)^2 \ge 0, \end{array} \]

due to the Cauchy-Schwartz inequality.