Orthogonal complement of a subspace

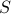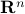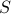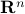Let be a subspace of $mathbf{R}^n$ . The orthogonal complement of , denoted S^perp , is the subspace of $mathbf{R}^n$ that contains the vectors orthogonal to all the vectors in .

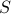If the subspace is described as the range of a matrix: $S = {Ax ::: x in mathbf{R}^n }$ , then the orthogonal complement is the set of vectors orthogonal to the rows of , which is the nullspace of A^T .

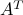Example: consider the line in 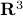$mathbf{R}^3$ passing through the origin and generated by the vector u=(1,2,3) . This is a subspace of dimension :

S = left{ tu ~:~ t in mathbf{R} right} = left{ left(begin{array}{c}t2t3tend{array}right) ~:~ t in mathbf{R} right} .

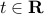To find the orthogonal complement we find the set of vectors that are orthogonal to any vector of the form , with arbitrary t in mathbf{R} . This is the same set as the set of vectors orthogonal to itself. So we solve for u^Tx = 0 with $x in mathbf{R}^3$ :

This is equivalent to x_1 = -2x_2-3x_3 . This equation characterizes the elements of the orthogonal complement S^perp , in the sense that any x in S^perp can be written as

x = left(begin{array}{c}-2alpha-3betaalphabetaend{array}right) = alpha u + beta v,

for some scalars 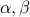alpha,beta , where

u = left( begin{array}{c}-210end{array}right), ;; v = left( begin{array}{c}-301end{array}right).

The orthogonal complement is thus the span of the vectors 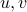u,v : $S^perp = mbox{bf span}(u,v)$ .