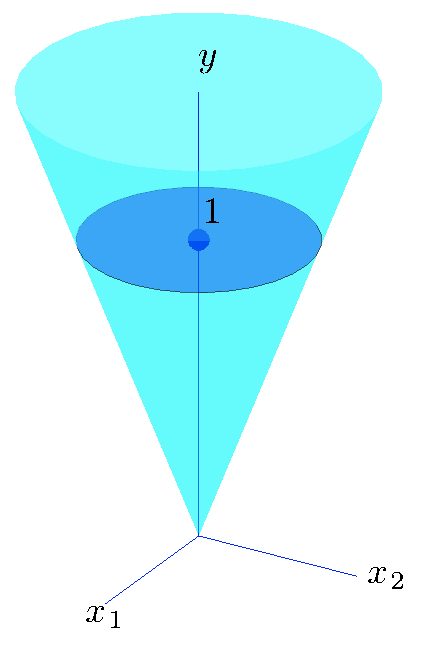
Second-order cone

Definition

The set in \(\mathbf{R}^{n+1}\)

\[ \mathbf{K}_{n} :=\left\{ (x,y) \in \mathbf{R}^{n+1}  :  y \ge \|x\|_2 \right\} \]

is a convex cone, called the second-order cone.

Example: The second-order cone is sometimes called ‘‘ice-cream cone’’. In \(\mathbf{R}^3\), it is the set of triples \((x_1,x_2,y)\) with \[ y^2 \ge x_1^2+x_2^2, \;\; y \ge 0. \] The blue circle corresponds to the set \[ \left\{ (x_1,x_2,y)  :  y = 1 \ge \sqrt{x_1^2+x_2^2} \right\}. \]

Proof of convexity

The fact that \(\mathbf{K}_{n}\) is convex can be proven directly from the basic definition of a convex set. Alternatively, we may express \(\mathbf{K}_{n}\) as an intersection of half-spaces, as follows.

From the Cauchy-Schwartz inequality, we have

\[ y \ge \|x\|_2 \Longleftrightarrow \forall \: u, \;\; \|u\|_2 \le 1  :  y \ge u^Tx , \]

we have

\[ \mathbf{K}_{n} = \bigcap_{u \::\: \|u\|_2 \le 1} \left\{ (x,y) \in \mathbf{R}^{n+1}  :  y \ge u^Tx \right\} . \]

Each one of the sets involved in the intersection is a half-space.