Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Definition: vector norm

Informally, a (vector) norm is a function which assigns a length to vectors.

Any sensible measure of length should satisfy the following basic properties: it should be a convex function of its argument (that is, the length of an average of two vectors should be always less than the average of their lengths); it should be positive-definite (always non-negative, and zero only when the argument is the zero vector), and preserve positive scaling (so that multiplying a vector by a positive number scales its norm accordingly).

Formally, a vector norm is a function 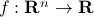f : mathbf{R}^n rightarrow mathbf{R} which satisfies the following properties.

Definition of a vector norm

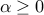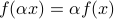  1. Positive homogeneity: for every x in mathbf{R}^n, alpha ge 0, we have f(alpha x) = alpha f(x).

  2. Triangle inequality: for every 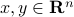x,y in mathbf{R}^n, we have

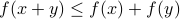
f(x+y) le f(x) + f(y)

  1. Definiteness: for every 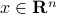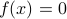xin mathbf{R}^n, f(x) = 0 implies x=0.

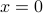A consequence of the first two conditions is that a norm only assumes non-negative values, and that it is convex.

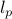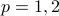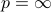Popular norms include the so-called l_p-norms, where p=1,2 or p=infty:

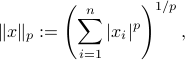
|x|_p := left( sum_{i=1}^n |x_i|^p right)^{1/p},

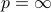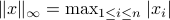with the convention that when p = infty, |x|_infty = max_{1 le i le n} |x_i|.