Separation of Ellipsoids
We consider the following geometrical problem: find a hyperplane that separates two ellipsoids in 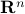 , or determine there is none.
, or determine there is none.
Putting a sphere in a half-space
We first seek a condition that determines wether the sphere of radius  centered at
centered at  is entirely contained in the half-space
is entirely contained in the half-space

where 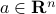 ,
, 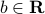 are given.
are given.
The condition is equivalent to the fact that

In view of the Cauchy-Schwartz inequality, we have

Clearly, the right-hand side is attained by some vector on the unit circle, namely  . Thus, the condition we seek is
. Thus, the condition we seek is

Putting an ellipsoid in a half-space
Now consider the case with an ellipsoid instead of a sphere. An ellipsoid 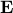 can be described as an affine transformation of the unit sphere:
can be described as an affine transformation of the unit sphere:

where  is the ‘‘center’’, and
is the ‘‘center’’, and 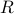 is a matrix that determines the ‘‘shape’’ of the ellipsoid.
is a matrix that determines the ‘‘shape’’ of the ellipsoid.
The containement condition  is equivalent to
is equivalent to

Using the same argument as before, we obtain the condition

Note that the condition that 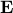 should be on the other side of the hyperplane is readily obtained by changing
should be on the other side of the hyperplane is readily obtained by changing 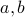 in
in  , that is:
, that is:

Ellipsoid separation
Now consider two ellipsoids

where  are the centers, and
are the centers, and 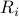 the shape matrices,
the shape matrices, 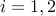 .
.
The hyperplane  separates the two ellipsoids if and only if
separates the two ellipsoids if and only if

Thus, the existence of such a separating hyperplane is equivalent to the existence of 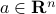 such that
such that

Exploiting the homogeneity with respect to  , we can always normalize the condition so that
, we can always normalize the condition so that  . The SOCP
. The SOCP

allows to determine if the ellipsoids are separable: they are if and only if  . In this case, an appropriate value of
. In this case, an appropriate value of 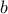 is
is

 |
Separating two ellipsoids by a hyperplane. |