QR decomposition: examples
Consider the  matrix
matrix

This matrix is full column rank. Indeed, the matlab command [Q,R]=qr(A,0) yields a 
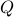 and a
and a 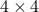
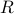 :
:


This shows that  is full column rank since
is full column rank since 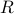 is invertible.
is invertible.
The command [Q,R]=qr(A) actually produces the full QR decomposition, with 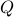 now a
now a 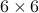 orthogonal matrix:
orthogonal matrix:


We can see what happens when the input is not full column rank: for example let's consider the matrix

( is not full column rank, as it was constructed so that the last column is a combination of the first and the third.)
is not full column rank, as it was constructed so that the last column is a combination of the first and the third.)
The (full) QR decomposition now yields:

We observe that the last triangular element is virtually zero, and the last column is seen to be a linear combination of the first and the third. This shows that the rank of 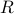 (itself equal to the rank of
(itself equal to the rank of  ) is effectively
) is effectively 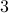 .
.