Portfolio Optimization via Linearly Constrained Least-Squares

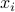We consider a universe of financial assets, in which we seek to invest over one time period. We denote by $r in mathbf{R}^n$ the vector containing the rates of return of each asset. A portfolio corresponds to a vector $x in mathbf{R}^n$ , where x_i is the amount invested in asset 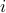. In our simple model, we assume that ‘‘shorting’’ (borrowing) is allowed, that is, there are no sign restrictions on .

As explained here, the return of the portfolio is the scalar product R(x) := r^Tx . We do not know the return vector in advance. We assume that we know a reasonable prediction hat{r} of . Of course, we cannot rely only on the vector hat{r} only to make a decision, since the actual values in could fluctuate around hat{r} . We can consider two simple ways to model the uncertainty on , which result in similar optimization problems.

Mean-variance trade-off

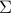A first approach assumes that is a random variable, with known mean hat{r} and covariance matrix Sigma . If past values r_1,ldots,r_N of the returns are known, we can use the following estimates

$hat{r} = frac{1}{N} sum_{i=1}^N r_i, ;; Sigma = frac{1}{N} sum_{i=1}^N (r_i-hat{r})(r_i-hat{r})^T.$

Note that, in practice, the above estimates for the mean hat{r} and covariance matrix Sigma are very unreliable, and more sophisticated estimates should be used.

Then the mean value of the portfolio's return R(x) takes the form $hat{R}(x) = hat{r}^Tx$ , and its variance is

$sigma(x)^2 := frac{1}{N} sum_{i=1}^N (r_i^Tx - hat{r}^Tx)^2 = x^T Sigma x.$

We can strike a trade-off between the ‘‘performance’’ of the portfolio, measured by the mean return, against the ‘‘risk’’, measured by the variance, via the optimization problem

$min_x : x^T Sigma x ~:~ hat{r}^Tx = mu,$

where 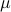is our target for the nominal return. Since 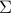Sigma is positive semi-definite, that is, it can be written as Sigma = A^TA with $A = (r_1-hat{r},ldots,r_N-hat{r})$ , the above problem is a linearly constrained least-squares.

An ellipsoidal model

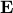To model the uncertainty in , we can use the following deterministic model. We assume that the true vector lies in a given ellipsoid mathbf{E} , but is otherwise unknown. We describe {cal E} by its center hat{r} and a ‘‘shape matrix’’ determined by some invertible matrix :

$mathbf{E} := left{ r = hat{r}+Lu ~:~ |u|_2 le 1 right}.$

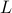We observe that if r in mathbf{E} , then r^Tx will be in an interval $[alpha_{rm min},alpha_{rm max}]$ , with

$alpha_{rm min} = min_{r in mathbf{E}} : r^Tx, ;; alpha_{rm max} = max_{r in mathbf{E}} : r^Tx .$

Using the Cauchy-Schwartz inequality, as well as the form of 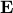mathbf{E} given above, we obtain that

$alpha_{rm max} = hat{r}^Tx + max_{u ::: |u|_2 le 1} : u^T(L^Tx) = hat{r}^Tx + |L^Tx|_2.$

Likewise,

$alpha_{rm min} = hat{r}^Tx - |L^Tx|_2.$

For a given portfolio vector , the true return r^Tx will lie in an interval $[hat{r}^Tx - sigma(x) , hat{r}^Tx + sigma(x)]$ , where $hat{r}^Tx$ is our ‘‘nominal’’ return, and is a measure of the ‘‘risk’’ in the nominal return:

We can formulate the problem of minimizing the risk subject to a constraint on the nominal return:

$min_x : x^T Sigma x ~:~ hat{r}^Tx = mu,$

where 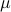is our target for the nominal return, and Sigma := LL^T . This is again a linearly constrained least-squares. Note that we obtain a problem that has exactly the same form as the stochastic model seen before.