Minimum Euclidean distance to a subspace: strong duality

Consider the problem of finding the minimum Euclidean distance to an affine subspace. The problem can be written as the convex problem

$p^ast = min_x : frac{1}{2}|x|_2^2 ~:~ Ax = b,$

for appropriate matrix 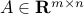$A in mathbf{R}^{m times n}$ and vector 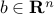$b in mathbf{R}^n$ . This problem does not have any inequality constraints. We assume that is full row rank (hence, AA^T succ 0 ), which guarantees that the problem is feasible for any choice of the vector .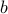

The dual function is

$g(nu) = min_x : frac{1}{2}|x|_2^2 + nu^T(b-Ax).$

Weak duality tells us that for any given , g(nu) is a lower bound on the optimal value of the primal problem:

For a given , the corresponding value of the dual function, g(nu) , can be computed explicitly, since it involves the unconstrained minimization of a convex (quadratic) function. In fact, there is a unique solution to the above problem: x(nu) := A^Tnu . Hence

$g(nu) = frac{1}{2}|x(nu)|_2^2 + nu^T(b-Ax(nu)) = b^Tnu - frac{1}{2} nu^T (AA^T) nu.$

The dual problem can also be solved explicitly, since it involves the unconstrained minimization of a convex (quadratic) function again. In fact, when is full row rank ( AA^T succ 0 ), the optimal is unique, and given by

$nu^ast = (AA^T)^{-1} b.$

Hence, the optimal value of the dual is

$d^ast = max_{nu} : g(nu) = frac{1}{2} b^T (AA^T)^{-1} b.$

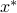We can check that strong duality holds for this problem. Indeed, Slater's condition holds (the problem is convex, has only affine equality constraints, and these are feasible). We can check this directly, and come up with an optimal point for the primal problem. To see this, we set $x^ast := x(nu^ast) = A^T(AA^T)^{-1}b$ . We then observe that x^ast is feasible, since Ax^ast = b , thus:

$d^ast le p^ast le frac{1}{2}|x^ast|_2^2.$

Since the corresponding value of the objective equals the lower bound 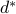d^ast , that is:

$frac{1}{2}|x^ast|_2^2 = frac{1}{2} b^T (AA^T)^{-1} b = d^ast,$

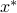we conclude that $p^ast le frac{1}{2}|x^ast|_2^2$ , that is, x^ast is indeed optimal for the primal problem.