Strong Duality for QP

Primal Problem

Consider the QP

$min_x : frac{1}{2} x^TQx +c^Tx ~:~ Ax le b,$

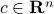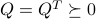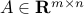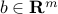where $c in mathbf{R}^n$ , $Q in mathbf{R}^{n times n}$ , Q = Q^T succeq 0 , $A in mathbf{R}^{m times n}$ , and $b in mathbf{R}^m$ . We assume for simplicity that Q succ 0 (that is, 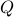is positive definite).

Dual problem

Let us form the dual of this problem. The Lagrangian is the function 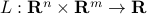$L : mathbf{R}^n times mathbf{R}^m rightarrow mathbf{R}$ with values

$L(x,lambda) = frac{1}{2} x^TQx + c^Tx + lambda^T(Ax-b),$

and the dual function is 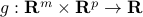$g : mathbf{R}^m times mathbf{R}^{p} rightarrow mathbf{R}$ , with values

$g(lambda) = min_x : L(x,lambda) = min_x : frac{1}{2} x^TQx + lambda^T(Ax-b).$

The above problem is an unconstrained convex optimization problem, so optimal points are characterized by the condition that the gradient of the objective is zero:

0 =nabla_x L(x,lambda) = Qx + c + A^T lambda.

Since 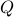is invertible, we obtain the minimizer as $x = -Q^{-1}A^Tlambda$ , and the dual function as

$g(lambda) = -lambda^Tb - frac{1}{2}(A^Tlambda +c)^TAQ^{-1}(A^Tlambda +c).$

The dual problem reads

$d^ast = max_{lambda ge 0} : g(lambda) = max_{lambda ge 0} : -lambda^Tb - frac{1}{2}(A^Tlambda +c)^TAQ^{-1}(A^Tlambda +c).$

The dual, just like the primal, is a QP.

We note that the dual feasible set has a particularly simple form, in contrast to that of the primal, which is a generic polytope.

Strong Duality Result

We can apply Slater's theorem to this QP, and obtain that a sufficient condition for strong duality to hold is that the QP is strictly feasible, that is, there exist 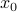x_0 such that Ax_0 <b .

However, if Q succ 0 , it can be shown that strong duality always holds.