Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Exercises

Convexity > Exercises

Convexity

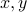  1. For x,y both positive scalars, show that

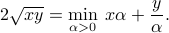
2 sqrt{xy} = min_{alpha >0} : x alpha + frac{y}{alpha}.

Justify carefully your approach. Use the above result to prove that the function f defined as

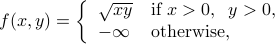
f(x,y) = left{ begin{array}{ll} sqrt{xy} & mbox{if } x>0, ;; y>0, -infty & mbox{otherwise,} end{array} right.

is concave.

  1. Show that for any numbers 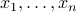x_1,ldots,x_n, we have

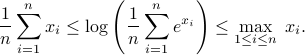
frac{1}{n} sum_{i=1}^n x_i le log left( frac{1}{n}sum_{i=1}^n e^{x_i} right) le max_{1 le i le n} : x_i .

  1. Consider the set defined by the following inequalities

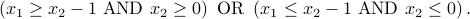
left( x_1 ge x_2 - 1 mbox{ AND } x_2 ge 0 right) mbox{ OR } left( x_1 le x_2 - 1 mbox{ AND } x_2 le 0 right).

    1. Draw the set. Is it convex?

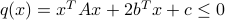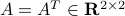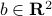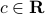    2. Show that it can be described as a single quadratic inequality of the form q(x) = x^TAx + 2b^Tx + c le 0, for matrix A=A^T in mathbf{R}^{2 times 2}, b in mathbf{R}^2 and c in mathbf{R} which you will determine.

    3. What is the convex hull of this set?

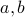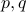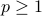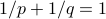  2. Prove Young's inequality, valid for every non-negative numbers a,b, and integers p,q with p ge 1, 1/p+1/q=1:

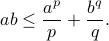
ab le frac{a^p}{p}+frac{b^q}{q}.

Hint: use the convexity of the exponential function.

Simple optimization problems

  1. Solve the optimization problems below: determine the optimal value and the optimal set.

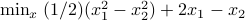    1. min_x : (1/2)(x_1^2 - x_2^2) + 2x_1 - x_2.

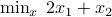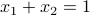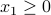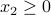    2. min_x : 2 x_1 + x_2 subject to x_1+x_2=1, x_1ge0, x_2ge0.

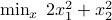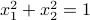    3. min_x : 2 x_1^2 + x_2^2 subject to x_1^2+x_2^2=1.

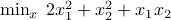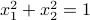    4. min_x : 2 x_1^2 + x_2^2 + x_1x_2 subject to x_1^2+x_2^2=1.

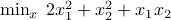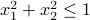    5. min_x : 2 x_1^2 + x_2^2 + x_1x_2 subject to x_1^2+x_2^2le1.

  2. Consider the optimization problem

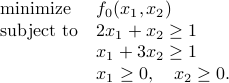
begin{array}{ll} mbox{minimize} &f_0(x_1,x_2) mbox{subject to} &2x_1+x_2 geq 1& x_1 +3x_2geq 1&x_1 geq 0, quad x_2geq 0. end{array}

Make a sketch of the feasible set. For each of the following objective functions, give the optimal set and the optimal value.

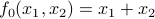    1. f_0(x_1,x_2) = x_1+x_2.

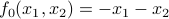    2. f_0(x_1,x_2) = -x_1-x_2.

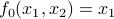    3. f_0(x_1,x_2) = x_1.

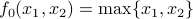    4. f_0(x_1,x_2) = max{x_1,x_2}.