Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Dual Problem

  • Primal problem

  • Lagrange function

  • Dual function

  • Dual problem

  • Remarks

Primal Problem

We consider a constrained optimization problem in standard form:

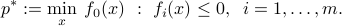
p^ast := min_x : f_0(x) ~:~ f_i(x) le 0, ;; i=1,ldots, m.

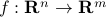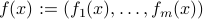We will refer to this problem as the primal problem. Its optimal value is the primal value, and x in mathbf{R}^n denotes the primal variables. We define f : mathbf{R}^n rightarrow mathbf{R}^m to be the constraint map, with values f(x):= (f_1(x),ldots,f_m(x)).

Example: the problem of finding the minimum distance to a polyhedron can be written as

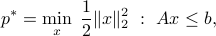
p^ast = min_x : frac{1}{2}|x|_2^2 ~:~ Ax le b,

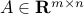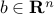for appropriate matrix A in mathbf{R}^{m times n} and vector b in mathbf{R}^n.

Lagrange function

We define the Lagrange function to be a function 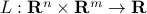L : mathbf{R}^n times mathbf{R}^m rightarrow mathbf{R} with values

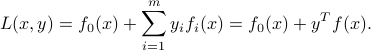
L(x,y) = f_0(x) + sum_{i=1}^m y_i f_i(x) = f_0(x) + y^Tf(x).

The Lagrange function depends on on the primal variables and an additional variable 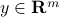y in mathbf{R}^m, referred to as the dual variable.

Example: The problem of minimum distance to a polyhedron above admits the Lagrangian

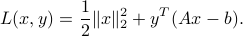
L(x,y) = frac{1}{2}|x|_2^2 + y^T(Ax-b).

Dual function

Based on the Lagrangian, we can build now a new function (of the dual variables only) that will provide a lower bound on the objective value.

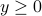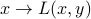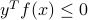For fixed y ge 0, we can interpret the partial function x rightarrow L(x,y) as a penalized objective, where violations of the constraints of the primal problem incur a penalty. The penalty grows linearly with the amount of constraint violation, and becomes positive only when one of the constraints is violated. Of course, if no constraint is violated, that is, if x is feasible, then y^Tf(x) le 0. Hence

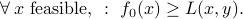
forall : x mbox{ feasible,} ~:~ f_0(x) ge L(x,y) .

Define the dual function 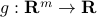g : mathbf{R}^m rightarrow mathbf{R} with values

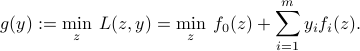
g(y) := min_z : L(z,y) = min_z : f_0(z) + sum_{i=1}^m y_i f_i(z).

Note that, since 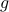g is defined as a point-wise minimum, it is a concave function.

We have, for any 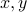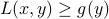x,y, L(x,y) ge g(y). Putting this together with the previous inequality, we get

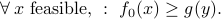
forall : x mbox{ feasible,} ~:~ f_0(x) ge g(y) .

That is, the dual function provides a lower bound on the objective value in the feasible set. The right-hand side of the above inequality is independent of x. Taking the minimum over x in the above, we obtain

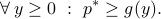
forall : y ge 0 ~:~ p^ast ge g(y).

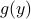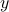Note that our lower bound may or may not be easy to compute. However, at first glance, computing g(y) with y fixed seems to be easier than the original problem, since there are no constraints.

Example: For the problem of minimum distance to a polyhedron above, the dual function is

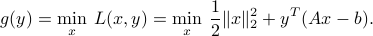
g(y) = min_x : L(x,y) = min_x : frac{1}{2}|x|_2^2 + y^T(Ax-b).

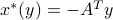In this case, the dual function can be computed explicitly. Indeed, the above problem is unconstrained, with a convex objective function (of x), hence global optima are characterized by setting the derivative with respect to x to zero. In this case, we obtain a unique optimal point x^ast(y) = -A^Ty. Replacing x by its optimal value, we obtain

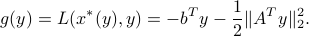
g(y) = L(x^ast(y),y) = -b^Ty - frac{1}{2}|A^Ty|_2^2.

Dual problem

Since the lower bound is valid for every 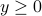y ge 0, we can search for the best one, that is, the largest lower bound:

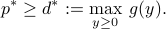
p^ast ge d^ast := max_{y ge 0} : g(y).

The problem of finding the best lower bound:

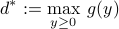
d^ast := max_{y ge 0} : g(y)

is called the dual problem associated with the Lagrangian defined above. It optimal value 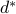d^ast is the dual optimal value. As noted above, 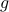g is concave. This means that the dual problem, which involves the maximization of 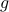g with sign constraints on the variables, is a convex optimization problem.

Example: For the problem of minimum distance to a polyhedron above, the dual problem is

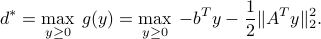
d^ast = max_{y ge 0} : g(y) = max_{y ge 0} : -b^Ty - frac{1}{2}|A^Ty|_2^2.

Problems with equality constraints

Equality constraints can be simply treated as two inequality ones. It turns out that this ends up being the same as if we simply remove sign constraints in the corresponding multiplier.

Remarks

Via duality, we can compute a lower bound on the optimal value of any problem, convex or not, using convex optimization. Several remarks attenuate the practical scope of the result:

  • The dual function 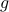g may not be easy to compute: it is itself defined as an optimization problem! Duality works best when 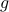g can be computed in closed form.

  • Even if it is possible to compute 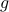g, it might not be easy to maximize: convex problems are not always easy to solve.

  • A lower bound might not be of great practical interest: often we need a sub-optimal solution. Duality does not seem at first to offer a way to compute such a primal point.

Despite these shortcomings, duality is an extremely powerful tool.

Examples:

  • Bounds on Boolean quadratic programming via Lagrange relaxation.