Exercises

Nullspace, rank and range

Determine the nullspace, range and rank of a 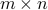matrix of the form

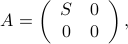
A = left( begin{array}{cc} S & 0 0 & 0end{array}right),

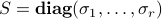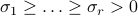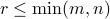where $S = mbox{bf diag}(sigma_1,ldots,sigma_r)$ , with sigma_1 ge ldots ge sigma_r>0 , and r le min(m,n) . In the above, the zeroes are in fact matrices of zeroes with appropriate sizes.

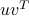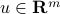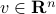Consider the matrix with $u in mathbf{R}^m$ , $v in mathbf{R}^n$ .
1. What is the size of ?
2. Determine the nullspace, the range, and the rank of .

Dimension of solution set

Determine the dimension of the sets of solutions to the following linear equations in a vector $x in mathbf{R}^n$ . Hint: use dyads and matrix notation.

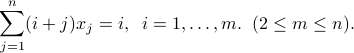
$sum_{j=1}^n (i+j) x_j = i,;; i=1,ldots,m. ;; (2 le m le n).$

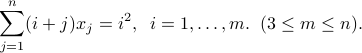
$sum_{j=1}^n (i+j) x_j = i^2,;; i=1,ldots,m. ;; (3 le m le n).$

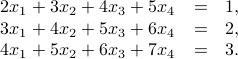
$begin{array}{rcl}2x_1+3x_2+4x_3+5x_4&=&1,3x_1+4x_2+5x_3+6x_4&=&2,4x_1+5x_2+6x_3+7x_4&=&3. end{array}$

Solving linear equations with multiple right-hand sides

Often it is of interest to be able to solve linear equations of the form 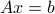Ax=b for many different instances of the output vector 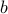. In this problem we assume that we are given 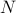such instances 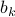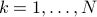b_k , k=1,ldots,N , which are collected as columns of a 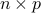n times p matrix 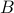. A direct approach to this task is encapsulated in the following matlab snippet:

n = 500; p = 100; A = randn(n); B = randn(n,p);
tic
for k=1:p
	b = B(:,k);
	x = A\b;
end
fprintf(’elapsed time = %10.7f\n’, toc)

Here is another approach:

n = 500; p = 100; A = randn(n); B = randn(n,p);
tic
[Q,R] = qr(A);
for k=1:p
	b = B(:,k);
	x = R\(Q’*b);
end
fprintf(’elapsed time = %10.7f\n’, toc)

Which method is faster? Justify your answer.

Polynomial interpolation

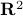In this problem, we look at a simple application of the range space for fitting a polynomial through a set of points. We are given points (x_1, y_1),ldots (x_n,y_n) in $mathbf{R}^2$ and we want to find a polynomial 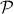mathcal{P} of degree 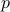such that, for all 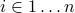i in 1ldots n , we have 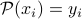$mathcal{P}(x_i) = y_i$ . That is, the polynomial must go through all the points. A polynomial 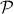of degree 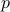is parametrized by the vector of its coefficients, that is:

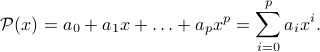
$mathcal{P}(x) = a_0 + a_1 x + dots + a_p x^p = sum_{i=0}^p a_i x^i.$

We assume that if 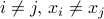i neq j, , x_i neq x_j .

What is the smallest value of 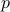that ensures that we will be able to fit any points? Would your answer be the same without the assumption that if 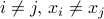? Explain briefly why the assumption is important or does not change the answer.
We are given a set of points. How can we compute the smallest value of 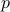such that there exists a polynomial that goes through all the points? How would you compute the coefficients 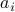of the polynomial?
We are told that the points were drawn from a polynomial of degree 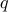and that up to one point is faulty (the polynomial does not go through this point). Is there a faulty point (discuss depending on the respective value of 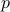and 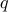)? If yes, how can you find it?