Exercises
Standard forms
Consider the two problems
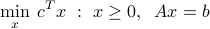
and
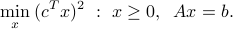
-
Show by a counterexample that these problems do not necessarily share the same set of optimal points.
Formulate the second problem as a linear program in standard form.
Show that if
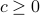 (that is, every component of
(that is, every component of  is non-negative), then the problems are equivalent.
is non-negative), then the problems are equivalent.
Consider a least-squares problem with linear inequality constraints
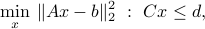
where 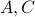 are given matrices (of row size equal to
are given matrices (of row size equal to  , the number of variables) and
, the number of variables) and 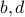 are given vectors.
are given vectors.
-
Write the problem as a QP in standard form.
Is the converse true? In other words, can we always transform a QP in standard form, into a problem with the form above? Discuss.
For given
 -vectors
-vectors 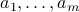 , consider the problem
, consider the problem
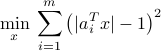
Proof or counter-example: the above problem is (a) an LP; (b) a QP; (c) An ordinary least-squares problem.
Applications
Computing the convex hull. In this exercise, you will devise an algorithm that, given a set of distinct
 points
points 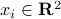 ,
, 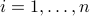 , plots the convex hull
, plots the convex hull 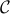 of the points. This well-studied problem arises a lot in computational geometry, see here.
of the points. This well-studied problem arises a lot in computational geometry, see here.Find a point
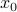 in the interior of the convex hull. Hint: think about the average of the points.
in the interior of the convex hull. Hint: think about the average of the points.Show how to formulate the following problem as a linear optimization problem: given a direction
 , find the largest
, find the largest 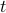 such that
such that 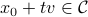 .
.Using CVX, plot the convex hull of the points in the matrix
![X = left[ begin {array}{cccccc} 15&6&8&5&6&3noalign{medskip}8&8&5&6&2&4end {array} right] .](eqs/2947323336651263633-130.png)
Hint: use the previous part with many directions  .
.
-
Comment on the accuracy needed when you scan the possible angular directions.
Can you come up with a more efficient method to solve this problem? Discuss.
A control problem. We consider a dynamical system with one input and one output, and described by a linear, time-invariant relationship:
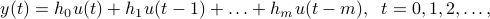
where 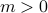 is the order of the system, and
is the order of the system, and 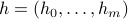 is called the impulse response. We consider an input design problem, where we seek to find a sequence of inputs which tracks a given desired output signal
is called the impulse response. We consider an input design problem, where we seek to find a sequence of inputs which tracks a given desired output signal 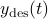 over a given time horizon
over a given time horizon 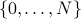 ,with
,with 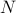 given. Specifically, we seek inputs
given. Specifically, we seek inputs 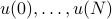 should be such that the following three conditions hold. (i) The peak deviation between
should be such that the following three conditions hold. (i) The peak deviation between 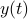 and
and 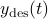
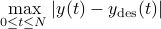
is minimized; (ii) the inputs should be zero for 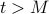 , where
, where 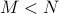 is given; (iii) the inputs should satisfy amplitude and slew rate constraints:
is given; (iii) the inputs should satisfy amplitude and slew rate constraints:
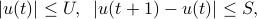
where 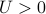 ,
, 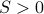 are given. Show that the problem can be formulated as a linear program.
Write a CVX code that plots the results given problem data.
are given. Show that the problem can be formulated as a linear program.
Write a CVX code that plots the results given problem data.
Advertising problem. A company wants to promote its newly developed product by launching an advertising campaign. There are four advertising options to choose from: TV Spot, Newspaper, Radio (prime time), and Radio (afternoon); these options are labelled
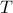 ,
, 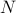 ,
, 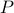 ,
,  , respectively. The table below provides, for each type of advertising, the audience reached, the cost and maximum number of ads per week. The company has a budget of $8000 per week and seeks to maximize audience reached. However, the company also wants
, respectively. The table below provides, for each type of advertising, the audience reached, the cost and maximum number of ads per week. The company has a budget of $8000 per week and seeks to maximize audience reached. However, the company also wants 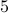 or more radio spots per week and cannot spend more than $1800 on radio per week. Let
or more radio spots per week and cannot spend more than $1800 on radio per week. Let 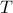 ,
, 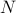 ,
, 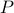 ,
,  be the decision variables corresponding to the numbers of ads chosen weekly by the company. (You can ignore the fact that these variables should be integers.) Formulate this as a linear programming problem, making sure to incorporate all the constraints in the formulation.
be the decision variables corresponding to the numbers of ads chosen weekly by the company. (You can ignore the fact that these variables should be integers.) Formulate this as a linear programming problem, making sure to incorporate all the constraints in the formulation.
| Advertising options | TV Spot (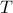 ) ) | Newspaper (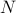 ) ) | Radio (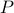 ) (prime time) ) (prime time) | Radio ( ) (afternoon) ) (afternoon) |
| Audience Reached (per ad) | 5000 | 8500 | 2400 | 2800 |
| Cost (per ad) | $ 800 | $ 925 | $ 290 | $ 380 |
| Max Ads (per week) | 12 | 5 | 25 | 20 |