State-space models of linear dynamical systems
Definition
Many discrete-time dynamical systems can be modeled via linear state-space equations, of the form

where  is the state, which encapsulates the state of the system at time
is the state, which encapsulates the state of the system at time 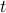 ,
,  contains control variables,
contains control variables,  contains specific outputs of interest, and
contains specific outputs of interest, and  are matrices of appropriate size.
are matrices of appropriate size.
In effect, a linear dynamical model postulates that the state at the next instant is a linear function of the state at past instants, and possibly other ‘‘exogeneous’’ inputs; and that the output is a linear function of the state and input vectors.
A continuous-time model would take the form of a differential equation

Finally, the so-called time-varying models involve time-varying matrices  (see an example below).
(see an example below).
Motivation
The main motivation for state-space models is to be able to model high-order derivatives in dynamical equations, using only first-order derivatives, but involving vectors instead of scalar quantities.
The above involves second-order derivatives of a scalar function  . We can express it in an equivalent form involving only first-order derivatives, by defining the state vector to be
. We can express it in an equivalent form involving only first-order derivatives, by defining the state vector to be

The price we pay is that now we deal with a vector equation instead of a scalar equation:

The position 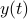 is a linear function of the state:
is a linear function of the state:

with  .
.
A nonlinear system
In the case of non-linear systems, we can also use state-space representations. In the case of autonomous systems (no external input) for example, these come in the form

where  is now a non-linear map. Now assume we want to model the behavior of the system near an equilibrium point
is now a non-linear map. Now assume we want to model the behavior of the system near an equilibrium point 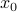 (such that
(such that  ). Let us assume for simplicity that
). Let us assume for simplicity that  .
.
Using the first-order approximation of the map  , we can write a linear approximation to the above model:
, we can write a linear approximation to the above model:

where

 |
The motion of a pendulum can be described by the dimensionless nonlinear equation 
The linearization around the equilibrium point |

 the external force acting on the mass, and
the external force acting on the mass, and 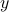 the vertical position. (Here
the vertical position. (Here  and
and  are the first and second derivatives of
are the first and second derivatives of  yields
yields  . The linearization around the equilibrium point
. The linearization around the equilibrium point  yields
yields  .
.