Optimization Models
Home
Software
Links
Index
Contact
1. Introduction
1.1. Overview
1.2. Optimization Models
2. Linear Algebra
2.1. Vectors
2.2. Matrices
2.3. Linear Equations
2.4.  Least-Squares
2.5. Eigenvalues
2.6  Singular Values
3. Convex Models
3.1. Convexity
3.2. LP and QP
3.3. SOCP
3.4. Robust LP
3.5. GP
3.6. SDP
3.7. Non-Convex Models
4. Duality
4.1. Weak Duality
4.2. Strong Duality
4.3.  Applications
5. Case Studies
5.1. Senate Voting
5.2. Antenna Arrays
5.3. Localization
5.4. Circuit Design

Exercises

Optimization of ellipsoid shapes

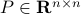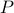  1. For P in mathbf{R}^{n times n}, with P symmetric and positive-definite, we define the ellipsoid

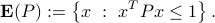
mathbf{E}(P) := left{ x ~:~ x^TP x le 1 right} .

A measure of the ‘‘size’’ of the ellipsoid is 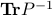mbox{bf Tr} P^{-1}, with 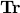mbox{bf Tr} the trace (the sum of the diagonal elements of the matrix argument).

    1. Motivate our choice of the size function. Hint: Figure out the the semi-axis lengths of the ellipsoid as a function of P.

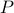    2. Show that 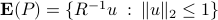mathbf{E}(P) = { R^{-1}u ::: |u|_2 le 1}, where 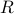R is a factor of 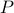P (any matrix 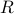R such that 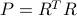P = R^TR; in matlab, 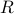R can be obtained via the command chol.)

    3. Show that for any 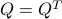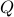Q=Q^T, Q positive-definite, the set 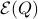{cal E}(Q) is contained in 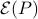{cal E}(P) if and only if 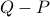Q-P is positive semi-definite.

    4. For given 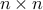n times n symmetric matrices 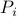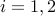P_i, i=1,2, both positive-definite, show how to compute an ellipsoid, centered at the origin, that contains both 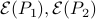{cal E}(P_1),{cal E}(P_2) and has minimum size.

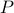    5. Implement and plot your result with the data contained in here. (The function P rightarrow mbox{bf Tr} P^{-1} for P symmetric and positive definite, is implemented in CVX using trace_inv.)