Exercises

SOCP > Exercises

Second-order cones

Draw the set of points 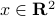$x in mathbf{R}^2$ such that 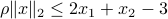, where 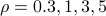. In general, for which values of 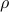, if any, is this set an ellipsoid? When is it not empty?
When considering a second-order cone constraint, a temptation might be to square it in order to obtain a classical convex quadratic constraint. This might not always work. Consider the convex, second-order cone:

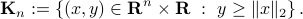
$mathbf{K}_n := left{ (x,y) in mathbf{R}^n times mathbf{R} ~:~ y ge |x|_2 right}.$

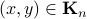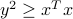If $(x,y) in mathbf{K}_n$ then y^2 ge x^Tx . Is the corresponding set

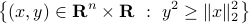
$left{ (x,y) in mathbf{R}^n times mathbf{R} ~:~ y^2 ge |x|_2^2 right}$

convex? Discuss.

Let 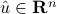$hat{u} in mathbf{R}^n$ and 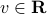, 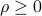be given. Consider the following condition on a given $x in mathbf{R}^n$ :

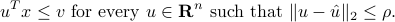
$u^Tx le v mbox{ for every } u in mathbf{R}^n mbox{ such that } |u-hat{u}|_2 le rho .$

1. Show that this condition is equivalent to a second-order cone condition on .
2. What is the geometrical interpretation of this condition?
3. Plot the set of 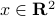$x in mathbf{R}^2$ that satisfy the condition with 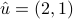, , and .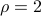

Standard forms

We would like to minimize the function 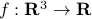$f : mathbf{R}^3 rightarrow mathbf{R}$ , with values:

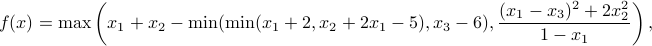
$f(x) = maxleft(x_1+x_2-min(min(x_1+2,x_2+2x_1-5), x_3 -6),frac{(x_1-x_3)^2+2x_2^2}{1-x_1}right),$

with the constraint 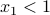x_1< 1 .

1. Explain precisely how to formulate the problem as an SOCP in standard form. Hint: Remember that 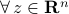$forall ,zin mathbf{R}^n$ , for all , 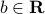non negative, the constraint 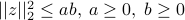is equivalent to a second order cone constraint.
2. Write a CVX code that solves the problem. Hint: use the function quad_over_lin.m.
Quadratically constrained quadratic programs are minimization problems involving convex quadratic objectives and constraints. This section shows that QCQP's can be expressed as SOCP's. Is the converse true, in other words, can we always write an SOCP as a QCQP? Discuss.
Robust least-squares. For a given matrix 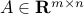$A in mathbf{R}^{m times n}$ and a vector 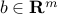$b in mathbf{R}^m$ , we consider the robust least-squares problem

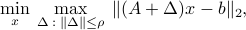
$min_x : max_{Delta ::: |Delta| le rho} : |(A+Delta)x - b|_2,$

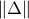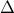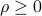where |Delta| denotes the largest singular value of the matrix Delta , and rho ge 0 is given. This problem arises when we seek to solve a least-squares problem in which the matrix is subject to an additive perturbation, and we would like to find a solution that minimizes the worst-case residual error.

1. Prove that for any given vectors 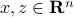$x,z in mathbf{R}^n$ , we have 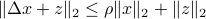whenever .
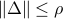2. Show that the bound you found in part (a) is attained, by exhibiting a matrix 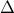that achieves the bound. Hint: use a rank-one matrix constructed with .
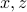3. Formulate the robust least-squares problem as an SOCP in standard form.
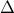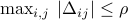4. Solve the problem in the case when the bound on the perturbation is a component-wise bound, of the form $max_{i,j} : |Delta_{ij}| le rho$ .

Applications

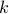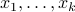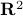Consider points in $mathbf{R}^2$ . For a given positive number 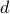, we define the 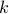-ellipse with radius 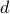as the set of points 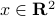$x in mathbf{R}^2$ such that the sum of the distances from to the points 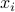is equal to .
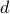1. How do 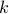-ellipses look like when 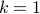or ?
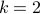2. Express the problem of computing the geometric median, which is the point that minimizes the sum of the distances to the points 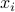, , 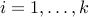as an SOCP in standard form.
3. Using CVX, write a code with input 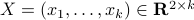$X=(x_1,ldots,x_k) in mathbf{R}^{2 times k}$ that plots the corresponding 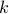-ellipse.